Samacheer Kalvi 11th Maths Guide Chapter 7 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 7.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 7.2 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 7 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 7.2

Question 1.
அணிக்கோவையை விரிவுபடுத்தாமல், \(\left|\begin{array}{lll}
s & a^{2} & b^{2}+c^{2} \\
s & b^{2} & c^{2}+a^{2} \\
s & c^{2} & a^{2}+b^{2}
\end{array}\right|\) = 0 என நிறுவுக.
தீர்வு :
∆ = \(\left|\begin{array}{lll}
s & a^{2} & b^{2}+c^{2} \\
s & b^{2} & c^{2}+a^{2} \\
s & c^{2} & a^{2}+b^{2}
\end{array}\right|\) என்க.
= s \(\left|\begin{array}{lll}
1 & a^{2} & b^{2}+c^{2} \\
1 & b^{2} & c^{2}+a^{2} \\
1 & c^{2} & a^{2}+b^{2}
\end{array}\right|\)
C₁ லிருந்து S வெளியில் எடுக்கப்பட்டுள்ளது.

= s\(\left|\begin{array}{lll}
1 & a^{2} & a^{2}+b^{2}+c^{2} \\
1 & b^{2} & a^{2}+b^{2}+c^{2} \\
1 & c^{2} & a^{2}+b^{2}+c^{2}
\end{array}\right|\) C₃ → C₂ + C₃
= s(a² + b² + c²)\(\left|\begin{array}{lll}
1 & a^{2} & 1 \\
1 & b^{2} & 1 \\
1 & c^{2} & 1
\end{array}\right|\)

(a² + b² + c ²) C₃ லிருந்து வெளியில் எடுக்கப்பட்டுள்ளது.
= s (a² + b² + c²) (0) (∵ C₁ = C₃)
= 0 = RHS.

Question 2.
\(\left|\begin{array}{lll}
b+c & b c & b^{2} c^{2} \\
c+a & c a & c^{2} a^{2} \\
a+b & a b & a^{2} b^{2}
\end{array}\right|\) = 0 என நிறுவுக.
தீர்வு :
∆ = \(\left|\begin{array}{lll}
b+c & b c & b^{2} c^{2} \\
c+a & c a & c^{2} a^{2} \\
a+b & a b & a^{2} b^{2}
\end{array}\right|\)
R₁, R₂, R₃ ஐ முறையே a, b, c ஆல் முறையே abc ஆல் எடுக்க

∆ = \(\frac{1}{a b c}\left|\begin{array}{lll}
a b+a c & a b c & a b^{2} c^{2} \\
b c+a b & a b c & a^{2} b c^{2} \\
a c+b c & a b c & a^{2} b^{2} c
\end{array}\right|\)

= \(\frac{(a b c)^{2}}{a b c}\left|\begin{array}{lll}
a b+a c & 1 & b c \\
b c+a b & 1 & a c \\
a c+b c & 1 & a b
\end{array}\right|\)
C₂, C₃ யிலிருந்து abc ஐ வெளியில் எடுக்க

= abc\(\left|\begin{array}{lll}
a b+b c+c a & 1 & b c \\
a b+b c+c a & 1 & a c \\
a b+b c+c a & 1 & a b
\end{array}\right|\) C₁ → C + C₃

= abc(ab + bc + ca)\(\left|\begin{array}{lll}
1 & 1 & b c \\
1 & 1 & a c \\
1 & 1 & a b
\end{array}\right|\)
C₁ லிருந்து (ab + bc + ca) ஐ வெளியில் எடுக்க
= abc (ab + be + ca) (0) = 0
[∵ C₁, C₂ சர்வசமம் பண்பு 4-ன் படி ]
= 0 = RHS.

Question 3.
\(\left|\begin{array}{ccc}
a^{2} & b c & a c+c^{2} \\
a^{2}+a b & b^{2} & a c \\
a b & b^{2}+b c & c^{2}
\end{array}\right|\) = 4a²b²;c² என நிறுவுக.
தீர்வு :
LHS = \(\left|\begin{array}{ccc}
a^{2} & b c & a c+c^{2} \\
a^{2}+a b & b^{2} & a c \\
a b & b^{2}+b c & c^{2}
\end{array}\right|\) = abc \(\left|\begin{array}{ccc}
a & c & a+c \\
a+b & b & a \\
b & b+c & c
\end{array}\right|\)
C₁, C₂ C₃ லிருந்து முறையே a,b,c ஐ வெளியில் எடுக்க ,

= abc\(\left|\begin{array}{ccc}
2(a+c) & c & a+c \\
2(a+b) & b & a \\
2(b+c) & b+c & c
\end{array}\right|\) C₁ → C₁ + C₂ + C₃

= 2 abc\(\left|\begin{array}{ccc}
(a+c) & c & a+c \\
(a+b) & b & a \\
(b+c) & b+c & c
\end{array}\right|\)

C₁ லிருந்து 2 ஐ வெளியில் எடுக்க,

C₁, C₂, C₃லிருந்து முறையே c, a, b ஐ வெளியில் எடுக்க,
= 2a²b²c² [(1 – 0) + 1 (1) + 0]
= 2a²b²c² × 2 = 4a²b²c² = RHS
எனவே நிருபிக்கப்பட்டது.

Question 4.
\(\left|\begin{array}{rrr}
1+a & 1 & 1 \\
1 & 1+b & 1 \\
1 & 1 & 1+c
\end{array}\right|=a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\) என நிறுவுக.
தீர்வு :
∆ = \(\left|\begin{array}{ccc}
1+a & 1 & 1 \\
1 & 1+b & 1 \\
1 & 1 & 1+c
\end{array}\right|\)

= \(\left|\begin{array}{rrr}
a & -b & 0 \\
0 & b & -c \\
1 & 1 & 1+c
\end{array}\right|\)
R₁ = R₁ – R₂
R₂ = R₂ – R₃
R₃ = R₃

= a [b+(1 + c) + c] + b(0 + c)
= a(b + bc + c) + bc
ab + abc + ac + bc
= abc \(\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\) = RHS.

Question 5.
\(\left|\begin{array}{rrr}
\sec ^{2} \theta & \tan ^{2} \theta & 1 \\
\tan ^{2} \theta & \sec ^{2} \theta & -1 \\
38 & 36 & 2
\end{array}\right|\) = 0 என நிறுவுக.
தீர்வு :
∆ = \(\left|\begin{array}{rrr}
\sec ^{2} \theta & \tan ^{2} \theta & 1 \\
\tan ^{2} \theta & \sec ^{2} \theta & -1 \\
38 & 36 & 2
\end{array}\right|\)

= \(\left|\begin{array}{rrr}
\sec ^{2} \theta-\left(\tan ^{2} \theta+1\right) & \tan ^{2} \theta & 1 \\
\tan ^{2} \theta-\left(\sec ^{2} \theta-1\right) & \sec ^{2} \theta & -1 \\
38-(36+2) & 36 & 2
\end{array}\right|\)

C₁ → C₁ – C₂ – C₃

= \(\left|\begin{array}{rrr}
0 & \tan ^{2} \theta & 1 \\
0 & \sec ^{2} \theta & -1 \\
0 & 36 & 2
\end{array}\right|\) = 0 = RHS

Question 6.
\(\left|\begin{array}{rrr}
x+2 a & y+2 b & z+2 c \\
x & y & z \\
a & b & c
\end{array}\right|\) = 0 என நிறுவுக.
தீர்வு :
∆ = \(\left|\begin{array}{rrr}
x+2 a & y+2 b & z+2 c \\
x & y & z \\
a & b & c
\end{array}\right|\)
= (x + 2a) (yc – bz) – (y + 2b) (xc – az) + (z + 2e) (bx – ay)
= xyc + 2ayc – bxz – 2abz – xyc – 2bxc + ayz + 2abz + bxz + 2bxc – ayz – 2acy
= 0 = RHS

Question 7.
3 × 3 வரிசை உடைய எதிர் சமச்சீர் அணியின்பொது வடிவத்தை எழுதுக. அதன் அணிக்கோவையின் மதிப்பு 0 எனக் காட்டுக.
தீர்வு :
\(\left[\begin{array}{ccc}
0 & a_{12} & a_{13} \\
-a_{12} & 0 & a_{23} \\
-a_{13} & -a_{23} & 0
\end{array}\right]_{3 \times 3}\)

∆ = \(\left|\begin{array}{ccc}
0 & a_{12} & a_{13} \\
-a_{12} & 0 & a_{23} \\
-a_{13} & -a_{23} & 0
\end{array}\right|\)
= 0[0 + (a₂₃)²] – a₁₂[0 + a₁₃a₂₃] + a₁₃[a₁₂a₂₃ – 0]
=

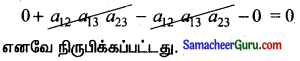
Question 8.
\(\left|\begin{array}{rrr}
a & b & a \alpha+b \\
b & c & b \alpha+c \\
a \alpha+b & b \alpha+c & 0
\end{array}\right|\) = 0 எனில் , a, b, c என்பன G.P. -ல் அமையும் அல்லது α என்பது ax² + 2bx + c = 0-ன் ஒரு மூலமாகும் என நிறுவுக.
தீர்ன :
a[0 – (bα + c)²] – b[(-aα + b) (bα + c)] + (aα + b) [b(bα + c) – c(aα + b)] = 0
-a(bα + c)² + b(aα + b) (bα + c) + b (aα + b) (bα + c) – c(aα + b)² = 0
(bα + c)[-a(bα + c) + b(aα + b)] + (aα + b)[b(bα + c) – c(aα + b)] = 0

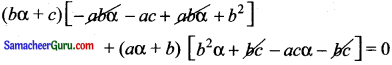
(bα + c)[b² – ac] + (aα + b)α(b² – ac) = 0
(b² – ac) [bα + c + (α + b)α] = 0
(b² – ac)[aα² + bα + bα + c] = 0
(b² – ac)[aα² + 2bα + c] = 0
b² – ac = 0 (அல்லது) a(அல்லது)² + 2b(அல்லது) + c = 0
b² = ac ∴ α என்பது
b= √ac ax² + 2bx + c = 0-ன் ஒரு மூலமாகும்
∴ a, b, Cஒரு G.P.

Question 9.
\(\left|\begin{array}{lll}
1 & a & a^{2}-b c \\
1 & b & b^{2}-c a \\
1 & c & c^{2}-a b
\end{array}\right|\) = 0 என நிறுவுக.
தீர்வு :
∆ =\(\left|\begin{array}{lll}
1 & a & a^{2}-b c \\
1 & b & b^{2}-c a \\
1 & c & c^{2}-a b
\end{array}\right|\)
= 1 [b (c² – ab) – 1(b² – ca)] – a [1 (c² – ab) – 1 (b² – ca)] + (a² – bc) (c -b)
=
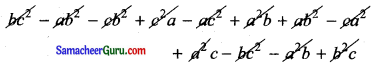
= 0 = RHS

Question 10.
a, b, c என்பன ஒரு A.P-ன் p, q மற்றும் r ஆவது உறுப்புகள் எனில், \(\left|\begin{array}{lll}
a & b & c \\
p & q & r \\
1 & 1 & 1
\end{array}\right|\)ன் மதிப்பு காண்க.
தீர்வு :
a = a + (p – 1)d
b = a + (q – 1)d
c = a + (r – 1)d

\(\left|\begin{array}{lll}
a & b & c \\
p & q & r \\
1 & 1 & 1
\end{array}\right|=\left|\begin{array}{rrr}
a+(p-1) d & a+(q-1) d & a+(r-1) d \\
p & q & r \\
1 & 1 & 1
\end{array}\right|\)

= \(\left|\begin{array}{ccc}
a & a & a \\
p & q & r \\
1 & 1 & 1
\end{array}\right|+\left|\begin{array}{rrr}
(p-1) d & (q-1) d & (r-1) d \\
p & q & r \\
1 & 1 & 1
\end{array}\right|\)

= 0 + d \(\left|\begin{array}{rrr}
(p-1) & (q-1) & (r-1) \\
p & q & r \\
1 & 1 & 1
\end{array}\right|\)
= d\(\left|\begin{array}{lll}
p & q & r \\
p & q & r \\
1 & 1 & 1
\end{array}\right|-\left|\begin{array}{lll}
1 & 1 & 1 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right|\)
= d(0) – 0 = 0

Question 11.
\(\left|\begin{array}{ccc}
a^{2}+x^{2} & a b & a c \\
a b & b^{2}+x^{2} & b c \\
a c & b c & c^{2}+x^{2}
\end{array}\right|\) என்ற அணிக்கோவை x⁴ஆல் வகுபடும் என நிறுவுக.
தீர்வு :
∆ = \(\left|\begin{array}{ccc}
a^{2}+x^{2} & a b & a c \\
a b & b^{2}+x^{2} & b c \\
a c & b c & c^{2}+x^{2}
\end{array}\right|\)
= [(a² + x²)[(b² + x²)(c² + x²) – b²c²] – ab[ab(c² + x²) – avc²] + ac [acb² – ac(b² + x²)]

= [(a² + x²)[b²c² + c²x² + b²x² + x⁴ – b²c²] – ab(abc² + ab – abc²) + a²c²b² – a²c²(9b² + x²)]

=
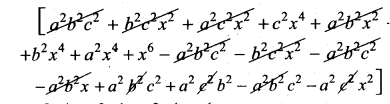
= c²x⁴ + b²x⁴ + a²x⁴ + x⁶
= x⁴(a² + b² + c²) + x⁶ இது x⁴ ஆல் வகுபடும்.

மாற்றுமுறை :

\(\left|\begin{array}{ccc}
a^{2}+x^{2} & a b & a c \\
a b & b^{2}+x^{2} & b c \\
a c & b c & c^{2}+x^{2}
\end{array}\right|\) = \(\left|\begin{array}{lll}
a^{2} & a b & a c \\
a b & b^{2} & b c \\
a c & b c & c^{2}
\end{array}\right|+\left|\begin{array}{ccc}
x^{2} & 0 & 0 \\
0 & x^{2} & 0 \\
0 & 0 & x^{2}
\end{array}\right|=\left|\begin{array}{lll}
a^{2} & a b & a c \\
a b & b^{2} & b c \\
a c & b c & c^{2}
\end{array}\right|\) + x⁶

=

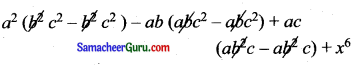
= 0 – 0 + 0 + x⁶
= x⁶ இது x⁴ ஆல் வகுபடும். எனவே நிருபிக்கப்பட்டது.

Question 12.
a, b, c என்பவை மிகை மற்றும் அவை ஒரு G.P.-ன் p, q மற்றும் 7-ஆவது உறுப்புகள் எனில், \(\left|\begin{array}{lll}
\log a & p & 1 \\
\log b & q & 1 \\
\log c & r & 1
\end{array}\right|\) என நிறுவுக.
தீர்வு :
a = ar^{p – 1}; b = ar^{q – 1}; c = ar^{r – 1}

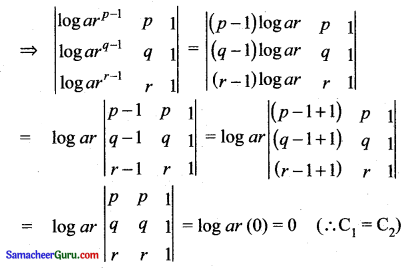
Question 13.
x, y, z # 1 எனில், \(\left|\begin{array}{rrr}
1 & \log _{x} y & \log _{x} z \\
\log _{y} x & 1 & \log _{y} z \\
\log _{z} x & \log _{z} y & 1
\end{array}\right|\) -ன் மதிப்பு காண்க.
தீர்வு :
\(\left|\begin{array}{rrr}
1 & \log _{x} y & \log _{x} z \\
\log _{y} x & 1 & \log _{y} z \\
\log _{z} x & \log _{z} y & 1
\end{array}\right|\)

= 1(1 – log_zy . log_yz) – log_xy (log_yx – log_zx . log_yz) + log_xz[log_yx log_zy – log_zx]

Question 14.
A = \(\left[\begin{array}{cc}
\frac{1}{2} & \alpha \\
0 & \frac{1}{2}
\end{array}\right]\) களில், \(\sum_{k=1}^{n}\) det(A^k) = \(\frac{1}{3}\)(1 – \(\frac{1}{4^{n}}\)) என நிறுவுக.
தீர்வு :
|A| = \(\left[\begin{array}{cc}
\frac{1}{2} & \alpha \\
0 & \frac{1}{2}
\end{array}\right]\) = \(\frac{1}{2}\) × \(\frac{1}{2}\) – 0 = \(\frac{1}{4}\)
det A¹ = \(\frac{1}{4}\)
det A² = (\(\frac{1}{4}\))²
det A³ = (\(\frac{1}{4}\))³
\(\frac{1}{4}\) + (\(\frac{1}{4}\))² + (\(\frac{1}{4}\))³ ……….

r = \(\frac{1}{4}\) < 1
S_n = \(\frac{a\left(1-r^{n}\right)}{1-r}\)
S_n =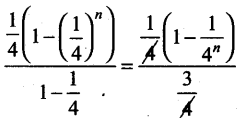
= \(\frac{1}{3}\)(1 – \(\frac{1}{4^{n}}\)) எனவே நிருபிக்கப்பட்டது.

Question 15.
விரிவுபடுத்தாமல் பின்வரும் அணிக்கோவைகளின் மதிப்பைக் காண்க.
(i) \(\left|\begin{array}{rrr}
2 & 3 & 4 \\
5 & 6 & 8 \\
6 x & 9 x & 12 x
\end{array}\right|\) (ii) \(\left|\begin{array}{rrr}
x+y & y+z & z+x \\
z & x & y \\
1 & 1 & 1
\end{array}\right|\)
தீர்வு :
(i) A = \(\left|\begin{array}{rrr}
2 & 3 & 4 \\
5 & 6 & 8 \\
6 x & 9 x & 12 x
\end{array}\right|\)

|A| = 3x\(\left|\begin{array}{lll}
2 & 3 & 4 \\
5 & 6 & 8 \\
2 & 3 & 4
\end{array}\right|\)
3x ஐ R₃ லிருந்து வெளியில் எடுக்க)
= 3x (0) = 0 [∵ R₁ = R₃]

(ii) A = \(\left|\begin{array}{rrr}
x+y & y+z & z+x \\
z & x & y \\
1 & 1 & 1
\end{array}\right|\)
A = \(\left|\begin{array}{ccc}
x-z & y-x & z+x \\
z-x & x-y & y \\
0 & 0 & 1
\end{array}\right|\)
C₁ → C₁ – C₂, C₂ → C₂ – C3
= \(\left|\begin{array}{ccc}
-(z-x) & -(x-y) & z \\
z-x & x-y & y \\
0 & 0 & 1
\end{array}\right|\)

= (z – x)(x – y)\(\left|\begin{array}{ccc}
-1 & -1 & z \\
1 & 1 & y \\
0 & 0 & 1
\end{array}\right|\)
(z – x)ஐC₁ லிருந்தும் (x – y)ஐ C₂ விலிருந்தும் வெளியில் எடுக்க.
∴ A = (z – x) (x – y) \(\left[1\left[\begin{array}{cc}
-1 & -1 \\
1 & 1
\end{array}\right]\right]\)
= (z – x) (x – y) (-1 + 1)
= (z – x) (x – y) (0) = 0

Question 16.
A என்பது ஒரு சதுர அணி மற்றும் |A| = 2 எனில், |AA^T|-ன் மதிப்பைக் காண்க.
தீர்வு :
|AA^T| = |A||A^T| = |A||A| (∵ |A| = |A^T|)
= 2 × 2 = 4

Question 17.
A, B என்பன |A|= -1 மற்றும் |B| = 3, எனுமாறு உள்ள 3 வரிசை சதுர அணிகள் எனில், |3AB|-ன் மதிப்பைக் காண்க.
தீர்வு :
|3AB| = 3³|A|.|B|
= 3\(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\) × -1 × 3 = \(\left|\begin{array}{lll}
3 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3
\end{array}\right|\) × -1 × 3
= 3³ × -1 × 3 = 27 × 3 = -81

Question 18.
λ = -2 எனில், \(\left|\begin{array}{rrr}
0 & 2 \lambda & 1 \\
\lambda^{2} & 0 & 3 \lambda^{2}+1 \\
-1 & 6 \lambda-1 & 0
\end{array}\right|\)-ன் மதிப்பைக் காண்க.
தீர்வு :
A = \(\left|\begin{array}{rrr}
0 & 2 \lambda & 1 \\
\lambda^{2} & 0 & 3 \lambda^{2}+1 \\
-1 & 6 \lambda-1 & 0
\end{array}\right|\) என்க.
A -ல்λ = -2 என பிரதியிட
A = \(\left|\begin{array}{rrr}
0 & 2(-2) & 1 \\
(-2)^{2} & 0 & 3(-2)^{2}+1 \\
-1 & 6(-2)-1 & 0
\end{array}\right|\)

= \(\left|\begin{array}{rrr}
0 & -4 & 1 \\
4 & 0 & 13 \\
-1 & -13 & 0
\end{array}\right|\)
= 0(0 + 169) + 4 (0 + 13) + 1 (-52)
= 0 + 52 – 52 =0
மேலும் A ஒரு எதிர் சமச்சீர் அணியாகும். முதன்மை மூலைவிட்ட உறுப்புகள் 0 என்பதாலும் எதிர் சமச்சீர் அணி A-ன் அணிக்கோவை பூஜ்ஜியம் எனலாம்.

Question 19.
\(\left|\begin{array}{rrr}
1 & 4 & 20 \\
1 & -2 & 5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|\) = 0 என்ற சமன்பாட்டின் மூலங்களைக் காண்க .
தீர்வு :
A = \(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & 5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|\) = 0
⇒ 1(-10x² – 10x) – 4(5x² – 5) + 20(2x + 2) = 0
⇒ -10x² – 10x – 20x² + 20 + 40x + 40 = 0
⇒ -30x^{2,/sup> + 30x + 60 = 0
-x2 + x + 2 = 0
x2 – x – 2 = 0}

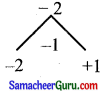
(x – 2) (x + 1) = 0
x = 2, -1

Question 20.
A = \(\left[\begin{array}{rrr}
4 & 3 & -2 \\
1 & 0 & 7 \\
2 & 3 & -5
\end{array}\right]\) மற்றும் B = \(\left[\begin{array}{rrr}
1 & 3 & 3 \\
-2 & 4 & 0 \\
9 & 7 & 5
\end{array}\right]\) என்ற அணிகளுக்கு det(AB) = (detA) (det B) என சரிபார்க்க .
தீர்வு :
AB = \(\left[\begin{array}{ccc}
4 & 3 & -2 \\
1 & 0 & 7 \\
2 & 3 & -5
\end{array}\right]\left[\begin{array}{ccc}
1 & 3 & 3 \\
-2 & 4 & 0 \\
9 & 7 & 5
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
(4-6-18) & (12+12-14) & (12+0-10) \\
(1+0+63) & (3+0+49) & (3+0+35) \\
(2-6-45) & (6+12-35) & (6+0-25)
\end{array}\right]\)

= \(\left|\begin{array}{ccc}
-20 & 10 & 2 \\
64 & 52 & 38 \\
-49 & -17 & -19
\end{array}\right|\)

|AB| = \(-20\left|\begin{array}{cc}
52 & 38 \\
-17 & -19
\end{array}\right|-10\left|\begin{array}{cc}
64 & 38 \\
-49 & -19
\end{array}\right|+2\left|\begin{array}{cc}
64 & 52 \\
-49 & -17
\end{array}\right|\)
= -20(-988 + 646) – 10(-1216 + 1862) + 2(-1088 + 2548)
= -20(-342) – 10(646) + 2(1460)
= 6840 – 6460 – 2920 = 3300 ……(1)

det(A) = \(\left|\begin{array}{ccc}
4 & 3 & -2 \\
1 & 0 & 7 \\
2 & 3 & -5
\end{array}\right|\)
= 4(0 – 21) – 3(-5 – 14) – 2(3 + 0)
= -84 – 3 × (-19) – 6
= -84 + 57 – 6
= -90 + 57 = -33

(det B) = \(\left|\begin{array}{ccc}
1 & 3 & 3 \\
-2 & 4 & 0 \\
9 & 7 & 5
\end{array}\right|\)
= 1(20 + 0) -3(-10 + 0) + 3(-14 – 36)
= 20 + 30 + 3 × -50
= 50 – 150 = -100

(det A) (det B) = -33(-100) = 3300 ………(2)
(1) = (2)
∴ det (AB) = (det A) (det B)

Question 21.
A = \(\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\) என்ற அணியின் இரண்டாம் நிரையில் உள்ள உறுப்புகளின் இணைக்காரணிகளைப் பயன்படுத்தி, |A| -ன் மதிப்பைக் காண்க.
தீர்வு :
A = \(\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\)
இரண்டாம் நிரையில் உள்ள உறுப்புகள் 2, 0, 1.

2-ன் இணைக்காரணி
A₂₁ = (-1)^{1 + 2}\(\left|\begin{array}{ll}
3 & 8 \\
2 & 3
\end{array}\right|\)
= (-1)³(9 – 16)
= (-1) × (-7) = 7

0-ன் இணைக்காரணி
A₂₂ = (-1)^{2 + 2}\(\left|\begin{array}{ll}
5 & 8 \\
1 & 3
\end{array}\right|\)
= (-1)⁴ (15 – 8) = 7

1-ன் இணைக்காரணி
A₂₃ = (-1)^{2 + 3}\(\left|\begin{array}{ll}
5 & 3 \\
1 & 2
\end{array}\right|\)
= (-1)⁵ (10 – 3) = -1 × 7
= -7
∴ |A| = a₂₁ A₂₁ + a₂₂ A₂₂ + a₂₃ A₂₃
= 2 × 7 + 0 × 7 + 1 × (-7) = 14 + 0 – 7 = 7