Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 7.3 Textbook Questions and Answers, Notes.
TN Board 11th Maths Solutions Chapter 7 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 7.3
பின்வருவனவற்றிற்கு காரணித் தேற்றத்தை பயன்படுத்துக :
Question 1.
\(\left|\begin{array}{lll}
x & a & a \\
a & x & a \\
a & a & x
\end{array}\right|\) = (x – a)2 (x + 2a) என நிறுவுக.
தீர்வு :
∆ = \(\left|\begin{array}{lll}
x & a & a \\
a & x & a \\
a & a & x
\end{array}\right|\) , x = a என ∆-ல் பிரதியிட
∴ ∆ = \(\left|\begin{array}{lll}
a & a & a \\
a & a & a \\
a & a & a
\end{array}\right|\) = 0
அனைத்து நிரைகளும் (3 நிரைகள்) சமம் என்பதால் (x – a)2 ஆனது ∆-ன் ஒரு காரணி ஆகும்.
x = -2a என ∆-ல் பிரதியிட
∆ = \(\left|\begin{array}{rrr}
-2 a & a & a \\
a & -2 a & a \\
a & a & -2 a
\end{array}\right|\) = \(\left|\begin{array}{rrr}
0 & a & a \\
0 & -2 a & a \\
0 & a & -2 a
\end{array}\right|\) = 0 [ ∵ C1 → C1 + C2 + C3]
∴ (x + 2a) ஒரு காரணியாகும்.
∴ (x – a)2 (x + 2a)1 ஆனது ∆-ன் காரணிகள் மற்றும் படியானது 3 ஆகும்.
முதன்மை மூலைவிட்டத்தின் பெருக்கற்பலனின் படியும் 3.
எனவே மற்றொரு காரணி k ஆக இருக்க வேண்டும்.
∴ \(\left|\begin{array}{lll}
x & a & a \\
a & x & a \\
a & a & x
\end{array}\right|\) = k (x – a)2 (x + 2a)
x3 – ன் உறுப்புகளை இருபுறமும் சமப்படுத்தி
1 = k
∴ \(\left|\begin{array}{lll}
x & a & a \\
a & x & a \\
a & a & x
\end{array}\right|\) = (x – a)2
![]()
Question 2.
\(\left|\begin{array}{lll}
b+c & a-c & a-b \\
b-c & c+a & b-a \\
c-b & c-a & a+b
\end{array}\right|\) = 8 abc என நிறுவுக.
தீர்வு :
∆ = \(\left|\begin{array}{lll}
b+c & a-c & a-b \\
b-c & c+a & b-a \\
c-b & c-a & a+b
\end{array}\right|\)
இங்கு a= 0 என பிரதியிட
= \(\left|\begin{array}{llr}
b+c & -c & -b \\
b-c & c & b \\
c-b & c & b
\end{array}\right|\)
C2, C3-யிலிருந்து c,b-ஐ வெளியில் எடுக்க
= bc\(\left|\begin{array}{lrr}
b+c & -1 & -1 \\
b-c & 1 & 1 \\
c-b & 1 & 1
\end{array}\right|\) = 0
⇒ ஒரு காரணியாகும். இதைப் போல் b,c யும் காரணிகளாகும். கொடுக்கப்பட்டுள்ள அணிக் கோவையின் முதன்மை மூலைவிட்ட பெருக்கற் பலனின் படியானது 3 ஆகும். எனவே மற்றொருபடி k ஆகும்.
∴ \(\left|\begin{array}{lll}
b+c & a-c & a-b \\
b-c & c+a & b-a \\
c-b & c-a & a+b
\end{array}\right|\) = k abc
இதில் a = 1, b = 1, c = 1 எனப் பிரதியிட
\(\left|\begin{array}{lll}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 2
\end{array}\right|\) = k × 1 × 1 × 1
⇒ k = 8
∴ ∆ = 8 abc
Question 3.
தீர்க்க : \(\left|\begin{array}{rrr}
x+a & b & c \\
a & x+b & c \\
a & b & x+c
\end{array}\right|\) = 0
தீர்வு :
∆ = \(\left|\begin{array}{rrr}
x+a & b & c \\
a & x+b & c \\
a & b & x+c
\end{array}\right|\) என்க.
இதில் x = 0 என்க.
∆ = \(\left|\begin{array}{lll}
a & b & c \\
a & b & c \\
a & b & c
\end{array}\right|\) = 0. மூன்று நிரைகளும் சர்வசமம்.
∴ x2 ஓர் காரணியாகும். மேலும் ∆-ல் x = -a – b – c என்க. –
∆ = \(\left|\begin{array}{rrr}
-b-c & b & c \\
a & -a-c & c \\
a & b & -a-b
\end{array}\right|\) இதில்
C1 = C1 + C2 + C3 எனில்
= \(\left|\begin{array}{rrr}
0 & b & c \\
0 & -a-c & c \\
0 & b & -a-b
\end{array}\right|\) = 0
∴ (x + a + b + c) ஒரு காரணியாகும். கொடுக்கப்பட்ட அணிக்கோவையின் படி 3. மற்றொரு காரணி k ஆக இருக்க வேண்டும்.
\(\left|\begin{array}{rrr}
x+a & b & c \\
a & x+b & c \\
a & b & x+c
\end{array}\right|\) = kx2(x + a + b + c) இதில்
a = 0, b = 1, c = 2, x = 1 எனப் பிரதியிட
\(\left|\begin{array}{lll}
1 & 1 & 2 \\
0 & 2 & 2 \\
0 & 1 & 3
\end{array}\right|\) = k(1)2 (1 +0 + 1 + 2)
(6 – 2) = k(4)
4 = 4k
k = 1
∴ \(\left|\begin{array}{rrr}
x+a & b & c \\
a & x+b & c \\
a & b & x+c
\end{array}\right|\) = x2 (x + a + b + c) = 0 என கொடுக்கப்பட்டுள்ளது.
⇒ x2 (x + a + b + c) = 0
⇒ x2 = 0 அல்லது (x + a + b + c) = 0
x = 0, 0 அல்லது
x = -a – b – c
x = -(a + b + c)
![]()
Question 4.
\(\left|\begin{array}{lll}
b+c & a & a^{2} \\
c+a & b & b^{2} \\
a+b & c & c^{2}
\end{array}\right|\) = (a + b + c) (a – b) (b – c) (c – a) என நிறுவுக.
தீர்வு :
\(\left|\begin{array}{lll}
b+c & a & a^{2} \\
c+a & b & b^{2} \\
a+b & c & c^{2}
\end{array}\right|=\left|\begin{array}{lll}
a+b+c & a & a^{2} \\
a+b+c & b & b^{2} \\
a+b+c & c & c^{2}
\end{array}\right|\) C1 → C1 + C2
= (a + b + c) \(\left|\begin{array}{lll}
1 & a & a^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|\)
(C1 லிருந்து (a + b + c) ஐ வெளியில் எடுக்க)
∆ = \(\left|\begin{array}{lll}
1 & b & b^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|\) என்க .
a = b என ∆-ல் பிரதியிட
= \(\left|\begin{array}{lll}
1 & b & b^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|\) = 0 ⇒ (a – b) ஒரு காரணி
இதைப்போலவே (b – c), (c – a)-ம் ∆-ன் காரணிகளாக அமையும்.
கொடுக்கப்பட்ட அணிக்கோவையின் படி 3.
∴ மற்றொரு காரணி k ஆக இருக்க வேண்டும்.
∴ a = 1, b = 2, c = 3 என
∆ = \(\left|\begin{array}{lll}
1 & a & a^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|\) = k(a – b) (b – c)(c – a)-ல் பிரதியிட
\(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 4 \\
1 & 3 & 9
\end{array}\right|\) = k(1 – 2) (2 – 3) (3 – 1)
1 (18 – 12) – 1(9 – 4) + 1 (3 – 2) = k(-1) (-1) (2)
6 – 5 + 1 = 2k
2 = 2k
⇒ k = 1
∴ \(\left|\begin{array}{lll}
1 & a & a^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|\) = (a – b) (b – c) (c – a)
∴ \(\left|\begin{array}{lll}
b+c_{1} & a & a^{2} \\
c+a & b & b^{2} \\
a+b & c & c^{2}
\end{array}\right|\) = (a + b + c)(a – b) (b – c) (c – a)
= RHS. எனவே நிருபிக்கப்பட்டது.
Question 5.
தீர்க்க : \(\left|\begin{array}{lll}
4-x & 4+x & 4+x \\
4+x & 4-x & 4+x \\
4+x & 4+x & 4-x
\end{array}\right|\) = 0
தீர்வு :
∆ = \(\left|\begin{array}{lll}
4-x & 4+x & 4+x \\
4+x & 4-x & 4+x \\
4+x & 4+x & 4-x
\end{array}\right|\) = 0
∆ = (4 – x) [(4 – x) – (4 + x) (4 + x)] – (4 + x) [[4 + x) (4 – x) – (4 + x)2] + (4 +x) [(4 + x)2]) – (4 + x) (4 – x)]
∆ = (4 – x) [(4 – x)2 – (4 + x)2] – (4 + x) [42 – x2 – (4 + x)2] + (4 + x) [(4 + x)2 – (42 – x2)] ;
∆ = (4 – x) [16 – 8x + x2 – (16 + 8x + x2) – (4 + x) (16 – x2 – (16 + 8x +x2) + (4 + x) [16 + 8x +x2 – (16 – x2)]
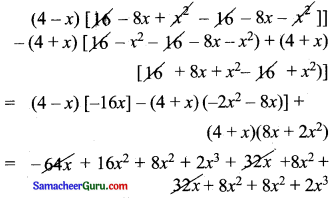
⇒ 48x2 + 4x3 = 0
4x2(12 + x) = 0
4x2 = 0 அல்ல து
(12 + x) = 0
x = 0, 0 அல்லது x = -12
∴ தீர்வு x = {0, 0, -12}
![]()
Question 6.
\(\left|\begin{array}{ccc}
1 & 1 & 1 \\
x & y & z \\
x^{2} & y^{2} & z^{2}
\end{array}\right|\) = (x – y) (y – z) (z – x) என நிறுவுக.
தீர்வு :
காரணித் தேற்றத்தைப் பயன்படுத்தி
∆ = \(\left|\begin{array}{lll}
1 & x & x^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right|\) என்க. (∴ பண்பு (1)-லிருந்து)
x = y என ∆- ல் பிரதியிட
= \(\left|\begin{array}{lll}
1 & y & y^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right|\) = 0 (∵ R1 = R2)
∴ (x – y) ஒரு காரணியாகும். இதைப் போலவே (y – z) (z – x) -ம் காரணிகளாகும்.
கொடுக்கப்பட்ட அணிக்கோவையின் படி 3 ஆகும்.
∴ மற்றொரு காரணி k எனக் கொள்வோம்.
∴ \(\left|\begin{array}{lll}
1 & x & x^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right|\) = k (x – y) (y – z) (z – k) இதில்
x = 1, y = 2, z = 3 எனப் பிரதியிட
\(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 4 \\
1 & 3 & 9
\end{array}\right|\) = k (1 – 2) (2 – 3) (3 – 1)
1 (18 – 12) -1 (9 – 4) + 1 (3 – 2) = 2k
6 – 5 + 1 = 2k
2 = 2k
⇒ k = 1
∴ \(\left|\begin{array}{lll}
1 & x & x^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right|\) = 1 (x – y) (y – z) (z – x)
⇒ ∆ = \(\left|\begin{array}{lll}
1 & x & x^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right|=\left|\begin{array}{rrr}
1 & 1 & 1 \\
x & y & z \\
x^{2} & y^{2} & z^{2}
\end{array}\right|\)
= (x – y) (y – z) (z – x) என நிருபிக்கப்பட்டது.