Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 8 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 8.2 Textbook Questions and Answers, Notes.
TN Board 11th Maths Solutions Chapter 8 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 8.2
Question 1.
கீழ்க்காணும் விகிதங்களை திசைக் கொசைன்களாக கொண்டு ஒரு வெக்டர் அமையுமா என சரிபார்க்க.
(i) \(\frac{1}{5}\), \(\frac{3}{5}\), \(\frac{4}{5}\)
(ii) \(\frac{1}{\sqrt{2}}\), \(\frac{1}{2}\), \(\frac{1}{2}\)
(iii) \(\frac{4}{3}\), 0, \(\frac{3}{4}\)
தீர்வு :
(i) கொடுக்கப்பட்டுள்ள விகிதங்கள் – \(\frac{1}{5}\), \(\frac{3}{5}\), \(\frac{4}{5}\)
l = \(\frac{1}{5}\), m = \(\frac{3}{5}\), n = \(\frac{4}{5}\)
∴ l2 + m2 + n2 = \(\left(\frac{1}{5}\right)^{2}+\left(\frac{3}{5}\right)^{2}+\left(\frac{4}{5}\right)^{2}\)
= \(\frac{1}{25}+\frac{9}{25}+\frac{16}{25}=\frac{1+9+16}{25}\)
= \(\frac{26}{25}\) ≠ 1
திசைக்கொசைன்களின் வர்க்கங்களின் கூடுதல் 1 ஆக இருக்க வேண்டும்.
∴ கொடுக்கப்பட்ட விகிதங்களை திசைக் கொசைன்களாகக் கொண்டு ஒரு வெக்டர் அமையாது.
(ii) l = \(\frac{1}{\sqrt{2}}\), m = \(\frac{1}{2}\), n = \(\frac{1}{2}\)
l2 + m2 + n2 = \(\left(\frac{1}{\sqrt{2}}\right)^{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}\)
= \(\frac{1}{2}+\frac{1}{4}+\frac{1}{4}\) = 1
∴ கொடுக்கப்பட்ட விகிதங்களை திசைக் கொசைன்களாகக் கொண்டு ஒரு வெக்டர் அமையும்.
(iii) l = \(\frac{4}{3}\), m = 0, n = \(\frac{3}{4}\)
l2 + m2 + n2 = \(\left(\frac{4}{3}\right)^{2}\) + 0 +\(\left(\frac{3}{4}\right)^{2}\)
= \(\frac{16}{9}\) + 0 + \(\frac{9}{16}\)
= \(\frac{256+81}{144}=\frac{337}{144}\) ≠ 0
∴ கொடுக்கப்பட்ட விகிதங்களை திசைக்கொசைன் களாகக் கொண்டு ஒரு வெக்டர் அமையாது.
Question 2.
கொடுக்கப்பட்ட திசை விகிதங்களைக் கொண்ட ஒரு வெக்டரின் திசைக் கொசைன்களைக் காண்க.
(i) 1, 2, 3 (ii) 3, -1, 3 (iii) 0, 0, 7
தீர்வு :
(i) x = 1, y = 2, z = 3
r = \(\sqrt{x^{2}+y^{2}+z^{2}}\) = \(\sqrt{1^{2}+2^{2}+3^{2}}\)
= \(\sqrt{1+4+9}=\sqrt{14}\)
∴ திசைக் கொசைன்கள் = \(\frac{x}{r}\), \(\frac{y}{r}\), \(\frac{z}{r}\)
= \(\frac{3}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}\)
(ii) x = 3, y = -1, z = 3
∴ r = \(\sqrt{x^{2}+y^{2}+z^{2}}\) = \(\sqrt{3^{2}+(-1)^{2}+3^{2}}\)
= \(\sqrt{9+1+9}=\sqrt{19}\)
∴ திசைக் கொசைன்கள் = \(\frac{x}{r}\), \(\frac{y}{r}\), \(\frac{z}{r}\)
= \(\frac{3}{\sqrt{19}}, \frac{-1}{\sqrt{19}}, \frac{3}{\sqrt{19}}\)
(iii) 0, 0, 7
x = 0, y = 0, z = 7
(ii) 0, 0, 7
x = 0, y = 0, z = 7
r = \(\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{0+0+7^{2}}\)
= √49 = 7
திசைக் கொசைன்கள் = \(\frac{x}{r}\), \(\frac{y}{r}\), \(\frac{z}{r}\)
= \(\frac{0}{7}\), \(\frac{0}{7}\), \(\frac{0}{7}\) = 0, 0, 1
![]()
Question 3.
கீழ்க்காணும் வெக்டர்களுக்குத் திசைக்கொசைன்கள், மற்றும் திசை விகிதங்களைக் காண்க.
(1) 3î – 4ĵ + 8k̂
(ii) 3î + ĵ+ k̂
(iii) ĵ
(iv) 5î – 3ĵ – 48k̂
(v) 3î – 3k̂ + 4ĵ
(vi) î – k̂
தீர்வு :
(i) 3î- 4ĵ + k̂ திசை விகிதங்கள் 3, -4, 8.
r = \(\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{3^{2}+(-4)^{2}+8^{2}}\)
= \(\sqrt{9+16+64}=\sqrt{89}\)
திசைக்கொசைன்கள் \(\frac{3}{\sqrt{89}}\), \(\frac{-4}{\sqrt{89}}\), \(\frac{8}{\sqrt{89}}\)
(ii) 3î + ĵ + k̂ திசைவிகிதங்கள் 3, 1, 1
x = 3, y = 1, z = 1
r = \(\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{3^{2}+1^{2}+1^{2}}=\sqrt{11}\)
திசைக்கொசைன்கள் = \(\frac{3}{\sqrt{11}}\), \(\frac{1}{\sqrt{11}}\), \(\frac{1}{\sqrt{11}}\)
(iii) \(\vec{j}=0 \vec{i}+\vec{j}+0 \vec{k}\)
திசைவிகிதங்கள் = 0, 1, 0.
r = \(\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{0^{2}+1^{2}+0^{2}}=\sqrt{1}\) = 1
திசைக்கொசைன்கள் = \(\frac{0}{1}\), \(\frac{1}{1}\), \(\frac{0}{1}\) = 0, 1, 0
(iv) 5î – 3ĵ – 48k̂
திசை விகிதங்கள் 5, – 3, – 48,
r = \(\sqrt{5^{2}+(-3)^{2}+(-48)^{2}}\) = \(\sqrt{25+9+2304}=\sqrt{2338}\)
திசைக்கொசைன்கள் \(\frac{5}{\sqrt{2338}}\), \(\frac{-3}{\sqrt{2338}}\), \(\frac{-48}{\sqrt{2338}}\)
(v) கொடுக்கப்பட்ட வெக்டர் k̂ – 3k + 4ĵ = 3î + 4ĵ – 3k̂
திசை விகிதங்கள் 3, 4, -3
r = \(\sqrt{3^{2}+4^{2}+(-3)^{2}}\)
= \(\sqrt{9+16+9}=\sqrt{34}\)
திசைக்கொசைன்கள் = \(\frac{3}{\sqrt{34}}\), \(\frac{4}{\sqrt{34}}\), \(\frac{-3}{\sqrt{34}}\)
(vi) கொடுக்கப்பட்ட வெக்டர் î – k̂= î + 0ĵ k̂
திசை விகிதங்கள் 1, 0, -1.
r = \(\sqrt{1^{2}+0^{2}+(-1)^{2}}=\sqrt{2}\)
திசைக்கொசைன்கள் = \(\frac{1}{\sqrt{2}}\), \(\frac{1}{\sqrt{2}}\), \(\frac{-1}{\sqrt{2}}\)
Question 4.
புள்ளிகள் (1,0,0), (0,1,0) மற்றும் (0, 0,1) ஆகியவற்றை முனைப் புள்ளிகளாகக் கொண்ட முக்கோணத்தின் நடுக்கோடுகளின் திசைக்கொசைன்களைக் காண்க,
தீர்வு :
A, B, C என்பன ∆ABC-யின் மூன்று முனைப்புள்ளிகள் D, E, F என்பன மூன்று பக்கங்கள் BC, CA, AC-யின் நடுப்புள்ளிகள்.
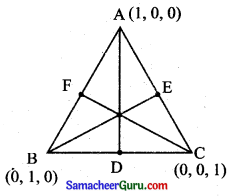
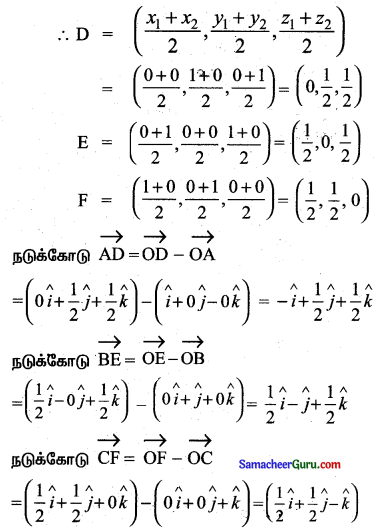
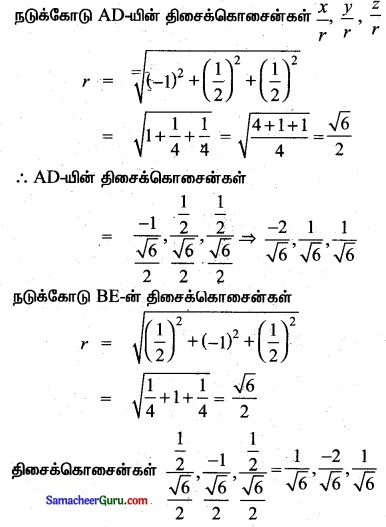
நடுக்கோடு CF
r = \(\sqrt{\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}+(-1)^{2}}\)
= \(\sqrt{\frac{1}{4}+\frac{1}{4}+1}=\frac{\sqrt{6}}{2}\)
திசைக்கொசைன்கள் \(\frac{\frac{1}{2}}{\frac{\sqrt{6}}{2}}, \frac{\frac{1}{2}}{\frac{\sqrt{6}}{2}}, \frac{-1}{\frac{\sqrt{6}}{2}}\) = \(\frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}}, \frac{-2}{\sqrt{6}}\)
![]()
Question 5.
\(\frac{1}{2}\), \(\frac{1}{\sqrt{2}}\), a ஆகியவை ஒரு வெக்டரின் திசைக்கொசைன் களாயின் a-ன் மதிப்பைக் காண்க.
தீர்வு :
\(x \vec{i}+y \vec{j}+z \vec{k}\) என்பது வெக்டர் என்க.
திசைக்கொசைன்கள் \(\frac{x}{r}\), \(\frac{y}{r}\), \(\frac{z}{r}\) = \(\frac{1}{2}\), \(\frac{1}{\sqrt{2}}\), a
⇒ l =\(\frac{x}{r}\), m = \(\frac{y}{r}\), n = \(\frac{z}{r}\) என்க
l2 + m2 + n2 = 1
∴ \(\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{\sqrt{2}}\right)^{2}\) + a2 = 1
⇒ \(\frac{1}{4}\) + \(\frac{1}{2}\) + a2 = 1
⇒ a2 = 1 – \(\frac{1}{4}\) – \(\frac{1}{2}\)
= \(\frac{4-1-2}{4}\) = \(\frac{1}{4}\)
a = ± \(\frac{1}{2}\)
Question 6.
(a, a + b , a + b + c) என்ப து (1, 0, 0) மற்றும் (0, 1, 0), ஆகியவற்றை இணைக்கும் கோட்டின் திசைவிகிதங்கள் எனில், a, b, c -ஐக் காண்க.
தீர்வு :
A(1, 0, 0), B(0, 1, 0)
\(\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\)
(கொடுக்கப்பட்ட கோட்டை AB எனக் கொண்டால்)
= (0î + ĵ + 0k̂) – (î + oĵ + ok̂)
= -î + ĵ இங்கு x = -1, y = 1, z = 0
∴ திசை விகிதங்கள் (-1, 1, 0) = (a, a + b, a + b + c)
a = -1, a + b = 1
⇒ -1 + b = 1,
⇒ b = 1 + 1 = 2
a+ b + c = 0
⇒ -1 + 2 + c = 0
⇒ c = 1 – 2 = -1
∴ (a, b, c) = (-1, 2,-1) கொடுக்கப்பட்ட கோடு BA என எடுத்துக் கொண்டால்
\(\overrightarrow{\mathrm{BA}}=\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\)
= (î + 0ĵ + 0k̂) – (0î + j + 0k̂)
= î – ĵ இங்கு x = 1, y = -1, z = 0
∴ திசை விகிதங்கள் (1, -1, 0) = (a, a + b, a + b + c)
a = 1, a + b = -1, 1 + b = -1
⇒ b = 1
⇒ a + b + c = 0 ⇒ 1 – 2 + c = 0 ⇒ c = 1
∴ a = 1, b = -2, c = 1
∴ திசைவிகிதங்கள் (a, b, c) = (1,-2, 1)
Question 7.
2î – ĵ + k̂, 3î – 4ĵ – 4k̂, î – 3j – 5k̂ஆகிய வெக்டர்கள் ஒரு செங்கோண முக்கோணத்தை அமைக்கும் எனக்காட்டுக.
தீர்வு :
Δ-ன் பக்கங்கள்

Question 8.
\(\vec{a}\) = 3î + 2ĵ + 9k̂ மற்றும் \(\vec{b}\) = î +λ ĵ + 3k̂ ஆகிய வெக்டர்கள் இணை எனில், λ-ன் மதிப்பைக் காண்க.
தீர்வு :
\(\vec{a}\) = 3î + 2ĵ + 9k̂
\(\vec{b}\) = î +λ ĵ + 3k̂
\(\vec{a}\) || \(\vec{b}\) எனில்,
\(\vec{a}\) = k\(\vec{b}\)
\(\vec{a}\) = 3î + 2ĵ + 9k̂ = 3(î + \(\frac{2}{3}\)ĵ + 3k̂) …………..(1)
\(\vec{a}\) = 3(î + λ ĵ + 3k̂
\(\vec{a}\) = 3\(\vec{b}\)
(1), (2) ஐ ஒப்பிட λ = \(\frac{2}{3}\)
![]()
Question 9.
கீழ்க்காணும் வெக்டர்கள் ஒரு தள வெக்டர்கள் எனக் காட்டுக.
(i) î – 2ĵ + 3k̂, -2î + 3ĵ – 4k̂, -ĵ + 2k̂
(i) 2î + 3î + k̂, î – ĵ, 7î + 3ĵ + 2k̂.
தீர்வு:
(i) \(\vec{a}\) = î – 2ĵ + 3k̂, \(\vec{b}\) = -2î + 3ĵ – 4k̂, \(\vec{c}\) = -ĵ + 2k̂
\(\vec{a}\) = s\(\vec{b}\) + t\(\vec{c}\) என எழுதலாம்.
⇒ î – 2ĵ + 3k̂ = s(-2î + 3ĵ – 4k̂) + t(0î -ĵ + 2k̂)கூறுகளை சமப்படுத்த
1 = -2s ⇒ -2s = 1 …………(1)
-2 = 3s – t ⇒ 3s – t = -2 ………(2)
3 = -4s + 2t ⇒ -4s + 2t = 3 …………(3)
(1) லிருந்து, = –\(\frac{1}{2}\)
(2) லிருந்து 3 × –\(\frac{1}{2}\) – t = -2
-t = -2 + \(\frac{3}{2}\) = \(\frac{-4+3}{2}=\frac{-1}{2}\)
t = \(\frac{1}{2}\)
s = –\(\frac{1}{2}\), t = \(\frac{1}{2}\) என (3) ல் பிரதியிட,
-4(-\(\frac{1}{2}\)) + 2(\(\frac{1}{2}\)) = 2 + 1 = 3 = RHS
∴ ஒரு வெக்டரை மற்ற இரு வெக்டர்களின் ஒருபடிச் சேர்ககையாக எழுதலாம். எனவே கொடுக்கப்பட்ட வெக்டர்கள் ஒரு தளத்தில் அமையும் வெக்டர்களாகும்.
(ii) Let \(\vec{a}\) = -2î + 3ĵ + k̂
\(\vec{b}\) = î – ĵ
\(\vec{c}\) = 7î + 3ĵ + 2k̂
\(\vec{a}\) = s\(\vec{b}\) + t\(\vec{c}\) என்க.
இங்கு மற்றும் t திசையிலிகள்
⇒ 2î + 3ĵ + k̂ = s(\(\vec{i}\) – \(\vec{j}\)) + t(7î + 3ĵ + 2k̂)
⇒ 2î + 3ĵ + k̂ = î(s + 7t) + ĵ(-s + 3t) + k̂(2t)
ஒத்த உறுப்புகளை ஒப்பிட கிடைப்பது
2 = s + 7t ……….(1)
3 = -s + 3t ………..(2)
1 = 2t ………..(3)
S மற்றும் t – ன் மதிப்புகளை காண, (2) மற்றும் (3) ஐ தீர்க்க
3) லிருந்து, t = \(\frac{1}{2}\)
t = \(\frac{1}{2}\) (2)- ல் பிரதியிட கிடைப்பது
3 = -s + 3(\(\frac{1}{2}\))
⇒ 3 = -s + \(\frac{3}{2}\)
⇒ s = \(\frac{3}{2}\) – 3 = \(\frac{3-6}{2}\) = –\(\frac{3}{2}\)
∴ t = \(\frac{1}{2}\) , s = –\(\frac{3}{2}\)
t = \(\frac{1}{2}\) மற்றும் s = –\(\frac{3}{2}\) என (1)ல் பிரதியிட கிடைப்பது
⇒ 2 = \(-\frac{3}{2}\) + 7(\(\frac{1}{2}\)) ⇒ 2 = \(-\frac{3}{2}\) + \(-\frac{7}{2}\)
⇒ 2 = \(\frac{-3 + 7}{2}\)
⇒ 2 = \(\frac{4}{2}\) ⇒ 2 = 2
∴ S மற்றும் 1-ன் மதிப்புகள் சமன்பாடு (1) ஐ நிறைவு செய்கிறது.
∴ ஒரு வெக்டரானது மற்ற இரு வெக்டர்களின் ஒருபடிச் சேர்க்கையாக எழுதலாம். எனவே கொடுக்கப்பட்ட வெக்டர்கள் ஒரு தள
வெக்டர்களாகும்.
Question 10.
4î + 5ĵ + k̂, -ĵ – k̂, 3î + 9ĵ + 4k̂ மற்றும் -4î + 4ĵ + 4k̂ ஆகியவற்றை நிலை வெக்டர்களாகக் கொண்ட புள்ளிகள் ஒரு தன அமைவன் எனக்காட்டுக.
நீர்வு :
\(\overrightarrow{\mathrm{OA}}\) = 4î + 5ĵ + k̂
\(\overrightarrow{\mathrm{OB}}\) = -ĵ – k̂
\(\overrightarrow{\mathrm{OC}}\) = 3î + 9ĵ + 4k̂
\(\overrightarrow{\mathrm{OD}}\) = -4î + 4ĵ + 4k̂ எனக
\(\vec{a}\) = \(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{OB}}\) – \(\overrightarrow{\mathrm{OA}}\)
= (-ĵ – k̂) – (4î + 5ĵ + k̂)
= -ĵ – k̂- 4î – 5ĵ – k̂
\(\vec{a}\) = -4î – 6ĵ – 2k̂
\(\vec{b}\) = \(\overrightarrow{\mathrm{AC}}\) = \(\overrightarrow{\mathrm{OC}}\) – \(\overrightarrow{\mathrm{OA}}\)
= 3î + 9ĵ + 4k̂ – 4î – 5ĵ – k̂
= -î + 4ĵ + 3k̂
\(\vec{c}\) = \(\overrightarrow{\mathrm{AD}}\) = \(\overrightarrow{\mathrm{OD}}\) – \(\overrightarrow{\mathrm{OA}}\)
= -4î + 4ĵ + 4k̂ – (4î + 5ĵ + k̂)
= -8î – ĵ + 3k̂
\(\vec{a}\) = s\(\vec{b}\) + t\(\vec{c}\) எனக
இருபுறமும் கூறுகளை சமப்படுத்த
-4 = -s – 8t ………..(1)
-6 = 4s – t …………(2)
-2 = 3s + 3t ………..(3)

t = \(\frac{2}{3}\), s = –\(\frac{4}{3}\) என (3) ல் பிரதியிட,
38 + 3t = 3 × \(-\frac{4}{3}\) + 3 × \(\frac{2}{3}\) = -4 + 2 = -2
∴ மூன்றாம் சமன்பாடு நிறைவு பெறுகிறது. ஆகவே ஒரு வெக்டரை மற்ற இரு வெக்டர்களின் ஒருபடிச் சேர்கையாக எழுதலாம். எனவே கொடுக்கப்பட்ட வெக்டர்கள் ஒரு தள அமைவன ஆகும்.
![]()
Question 11.
\(\vec{a}\) = 2î + 3ĵ – 4k̂, \(\vec{b}\) = 3î – 4ĵ – 5k̂, \(\vec{c}\) = -3î + 2ĵ + 3k̂
எனில், கீழ்க்காணும் வெக்டர் , களில் எண்ணளவையும் திசைக் கொசைன்களையும் காண்க.
(i) \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\) (ii) 3\(\vec{a}\) – 2\(\vec{b}\) + 5\(\vec{c}\)
தீர்வு :
(i) \(\vec{a}\) = 2î + 3ĵ – 4k̂
\(\vec{b}\) = 3î – 4ĵ – 5k̂
\(\vec{c}\) = -3î + 2ĵ + 3k̂
\(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\) = (2î + 3ĵ – 4k̂) + (3î – 4ĵ – 5k̂) + (-3î + 2ĵ + 3k̂)
|\(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\)| = \(\sqrt{2^{2}+1^{2}+(-6)^{2}}=\sqrt{4+1+36}\)
எண்ண ளவு = √41
திசைக்கொசைன்கள் = \(\frac{2}{\sqrt{41}}\), \(\frac{1}{\sqrt{41}}\), \(\frac{-6}{\sqrt{41}}\)
(ii) 3\(\vec{a}\) – 2\(\vec{b}\) + 5\(\vec{c}\) = 3(2î + 3ĵ – 4k̂) – 2(3î – 4ĵ – 5k) + 5(-3î + 2ĵ + 3k̂)
= 6î + 9ĵ – 12k̂ – 6î + 8ĵ + 10k̂ – 15î + 10ĵ + 15k̂ = -15î + 27ĵ + 13k̂
|3\(\vec{a}\) – 2\(\vec{b}\) + 5\(\vec{c}\)| = \(\sqrt{(-15)^{2}+27^{2}+13^{2}}\)
= \(\sqrt{225+729+169}\)
எண்ண ளவு = \(\sqrt{1123}\)
திசைக்கொசைன்கள் = \(\frac{-15}{\sqrt{1123}}\), \(\frac{27}{\sqrt{1123}}\), \(\frac{13}{\sqrt{1123}}\)
Question 12.
î + 2ĵ + 3k̂, 3î -4ĵ + 5k̂ மற்றும் -2î + 3ĵ – 7k̂ ஆகியவை ஒரு முக்கோணத்தின் முனைப்புள்ளிகளின் நிலை வெக்டர்கள் எனில், அந்த முக்கோணத்தின் சுற்றளவைக் காண்க.
தீர்வு :
\(\overrightarrow{\mathrm{OA}}\) = î + 2ĵ + 3k̂
\(\overrightarrow{\mathrm{OB}}\) = 3î -4ĵ + 5k̂
\(\overrightarrow{\mathrm{OC}}\) = -2î + 3ĵ – 7k̂
\(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{OB}}\) – \(\overrightarrow{\mathrm{OA}}\)
= (3î -4ĵ + 5k̂) – (î + 2ĵ + 3k̂) = 2î – 6ĵ + 2k̂
\(\overrightarrow{\mid A B} \mid\) = \(\sqrt{2^{2}+(-6)^{2}+2^{2}}\)
= \(\sqrt{4+36+4}=\sqrt{44}\)
\(\overrightarrow{\mathrm{BC}}\) = \(\overrightarrow{\mathrm{OC}}\) – \(\overrightarrow{\mathrm{OB}}\)
= (-2î + 3ĵ – 7k̂) – (3î -4ĵ + 5k̂) = -5î + 7ĵ – 12k̂
\(\overrightarrow{\mid B C} \mid\) = \(\sqrt{(-5)^{2}+7^{2}+(-12)^{2}}\)
= \(\sqrt{25+49+144}=\sqrt{218}\)
\(\overrightarrow{\mathrm{CA}}\) = \(\overrightarrow{\mathrm{OA}}\) – \(\overrightarrow{\mathrm{OC}}\)
= î + 2ĵ + 3k̂ – (-2î + 3ĵ – 7k̂)
= 3î – ĵ + 10k̂
\(\overrightarrow{\mid B C} \mid\) = \(\sqrt{(3)^{2}+(-1)^{2}+(10)^{2}}\)
= \(\sqrt{9+1+100}=\sqrt{110}\)
∆-யின் சுற்றளவு = |AB| +|BC| +|CA|
= (√44 + √218+ √110) அலகுகள்
![]()
Question 13.
\(\vec{a}\) = 3î – ĵ – 4k̂, \(\vec{b}\) = – 2î + 4ĵ – 3k̂, மற்றும் \(\vec{c}\) = î + 2ĵ – k̂ எனில், 3\(\vec{a}\) – 2\(\vec{b}\) + 4\(\vec{c}\) என்ற வெக்டருக்கு இணையான அலகு வெக்டரைக்
காண்க.
தீர்வு :
\(\vec{a}\) = 3î – ĵ – 4k̂
\(\vec{b}\) = – 2î + 4ĵ – 3k̂
\(\vec{c}\) = î + 2ĵ – k̂
3\(\vec{a}\) – 2\(\vec{b}\) + 4\(\vec{c}\) = 3(3î – ĵ – 4k̂) – 2(- 2î + 4ĵ – 3k̂) + 4(î + 2ĵ – k̂)
= 9î – 3ĵ – 12k̂ + 4î – 8ĵ + 6k̂ + 4î + 8ĵ – 4k̂
= 17î – 3ĵ – 10k̂
|3\(\vec{a}\) – 2\(\vec{b}\) + 4\(\vec{c}\)| = \(\sqrt{17^{2}+(-3)^{2}+(-10)^{2}}\)
= \(\sqrt{289+9+100}=\sqrt{398}\)
∴ 3\(\vec{a}\) – 2\(\vec{b}\) + 4\(\vec{c}\) என்ற வெக்டருக்கு இணையான அலகு வெக்டர் \(\frac{1}{\sqrt{398}}\) (17î – 3ĵ – 10k̂)
Question 14.
மூன்று புள்ளிகளின் நிலை வெக்டர்கள் \(\vec{a}\), \(\vec{b}\), \(\vec{c}\)
ஆகியவை 2\(\vec{a}\) – 7\(\vec{b}\) + 5\(\vec{c}\) = \(\vec{0}\)என்ற நிபந்தனையை நிறைவு செய்தால் அப்புள்ளிகள் ஒரே கோட்டில் அமையுமா எனக் கூறுக.
தீர்வு :
மூன்று புள்ளிகளின் நிலைவெக்டர்கள் \(\vec{a}\), \(\vec{b}\), \(\vec{c}\)
என்க.
2\(\vec{a}\) – 7\(\vec{b}\) + 5\(\vec{c}\) = 0
⇒ 2\(\vec{a}\) + 5\(\vec{c}\) = 7\(\vec{b}\)
⇒ \(\vec{b}\) = \(\frac{2}{7}\)\(\vec{a}\) + \(\frac{5}{7}\)\(\vec{b}\)
⇒ \(\vec{b}\) = s\(\vec{a}\) + s\(\vec{b}\)
b = s\(\vec{a}\) + s\(\vec{b}\)
∴ \(\vec{b}\) ஆனது இரு வேறு வெக்டர்களின் ஒருபடிச் சேர்க்கையாக எழுத முடியும் என்பதால் அவை ஒரே
கோட்டில் அமையும்.
![]()
Question 15.
P, Q, R, S என்ற புள்ளிகளின் நிலை வெக்டர்கள் முறையே (î + ĵ + k̂), (2î + 5ĵ), (3î + 2ĵ – 3k̂), மற்றும் (î – 6ĵ – k̂) எனில், PQ மற்றும் RS ஆகியவை இணை எனக்காட்டுக.
தீர்வு :
\(\overrightarrow{\mathrm{OP}}\) = î + ĵ + k̂
\(\overrightarrow{\mathrm{OQ}}\) = 2î + 5ĵ
\(\overrightarrow{\mathrm{OR}}\) = 3î + 2ĵ – 3k̂
\(\overrightarrow{\mathrm{OS}}\) = î – 6ĵ – k̂
\(\overrightarrow{\mathrm{PQ}}\) = \(\overrightarrow{\mathrm{OQ}}\) – \(\overrightarrow{\mathrm{OP}}\)
= 2î + 5ĵ – (î + ĵ + k̂) = î + 4ĵ – k̂
\(\overrightarrow{\mathrm{RS}}\) = \(\overrightarrow{\mathrm{OS}}\) – \(\overrightarrow{\mathrm{OR}}\)
= î – 6ĵ – k̂ – (3î + 2ĵ – 3k̂)
= -2î – 8ĵ + 2k̂
= -2(î + 4ĵ – k̂)
= -2\(\overrightarrow{\mathrm{PQ}}\)
∴ \(\overrightarrow{\mathrm{PQ}}\) || \(\overrightarrow{\mathrm{RS}}\)
∴ \(\overrightarrow{\mathrm{RS}}\) = λ\(\overrightarrow{\mathrm{PQ}}\)
λ = -2
Question 16.
m(î + ĵ + k̂) ஓர் அலகு வெக்டராயின் மதிப்புகளைக் காண்க.
தீர்வு :
\(\vec{a}\) = m(î + ĵ + k̂) என்க .
|\(\vec{a}\)| = m\(\sqrt{1^{2}+1^{2}+1^{2}}\) = m√3
\(\vec{a}\) ஓர் அலகு வெக்டராயின் |\(\vec{a}\)| = ±1
m√3 = ±1 ⇒ m = ±\(\frac{1}{\sqrt{3}}\).
![]()
Question 17.
A(1, 1, 1), B(1, 2, 3) மற்றும் C(2, -1, 1) ஆகிய புள்ளிகள் ஓர் இரு சமபக்க முக்கோலத்தின் முனைப்புள்ளிகள் என நிறுவுக.
தீர்வு :
A (1, 1, 1) ⇒ \(\overrightarrow{\mathrm{OA}}\) = î + ĵ + k̂
B(1, 2, 3) ⇒ \(\overrightarrow{\mathrm{OB}}\) = î + 2ĵ + 3k̂
C(2,-1, 1) ⇒ \(\overrightarrow{\mathrm{OC}}\) = 2î – ĵ +k̂
\(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{OB}}\) – \(\overrightarrow{\mathrm{OA}}\)
= î + 2ĵ + 3k̂ – (î + ĵ + k̂)
= ĵ + 2k̂
|\(\overrightarrow{\mathrm{AB}}\)| = \(\sqrt{1^{2}+2^{2}}=\sqrt{5}\)
\(\overrightarrow{\mathrm{BC}}\) = \(\overrightarrow{\mathrm{OC= }}\) – \(\overrightarrow{\mathrm{OB}}\)
= (2î – ĵ + k̂) – (î + 2ĵ + 3k̂)
= î – 3ĵ – 2k̂
|\(\overrightarrow{\mathrm{BC}}\)| = \(\sqrt{1^{2}+(-3)^{2}+(-2)^{2}}\)
= \(\sqrt{1+9+4}=\sqrt{14}\)
\(\overrightarrow{\mathrm{CA}}\) = \(\overrightarrow{\mathrm{OA}}\) – \(\overrightarrow{\mathrm{OC}}\)
= (î + ĵ + k̂) – (2î – ĵ +k̂)
= -î + 2ĵ
|\(\overrightarrow{\mathrm{CA}}\)| = \(\sqrt{(-1)^{2}+2^{2}}=\sqrt{5}\)
|AB| = |CA| = √5
கொடுக்கப்பட்ட புள்ளிகள் ஓர் இருசமபக்க ∆-ன் முனைப்புள்ளிகள் ஆகும்.