Samacheer Kalvi 11th Maths Guide Chapter 8 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 8.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 8 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 8.5 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 8 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 8.5

சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்.

Question 1.
\(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) + \(\overrightarrow{\mathrm{DA}}\) + \(\overrightarrow{\mathrm{CD}}\) என்பது
(1) \(\overrightarrow{\mathrm{AB}}\)
(2) \(\overrightarrow{\mathrm{CA}}\)
(3) \(\overrightarrow{0}\)
(4) –\(\overrightarrow{\mathrm{AD}}\)
குறிப்பு :
\(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) + \(\overrightarrow{\mathrm{DA}}\) + \(\overrightarrow{\mathrm{CD}}\) = \(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) + \(\overrightarrow{\mathrm{CD}}\) + \(\overrightarrow{\mathrm{DA}}\) = \(\overrightarrow{\mathrm{AA}}\) = \(\overrightarrow{0}\)
விடை:
(3) \(\overrightarrow{0}\)

Question 2.
\(\vec{a}\) + 2\(\vec{b}\) மற்றும் 3\(\vec{a}\) + m\(\vec{b}\) ஆகியவை இணை எனில், m -ன் மதிப்பு
(1) 3
(2) \(\frac{1}{3}\)
3) 6
(4) \(\frac{1}{6}\)
குறிப்பு :
\(\vec{a}\) + 2\(\vec{b}\) = 3(\(\vec{a}\) + 2\(\vec{b}\)) (∵ அவை இணை)
= 3\(\vec{a}\) + 6\(\vec{b}\) ……………(1)
(\(\vec{a}\) + 2\(\vec{b}\)) || 3\(\vec{a}\) + m\(\vec{b}\) ……….(2)
(1), (2) ஐ ஒப்பிட m = 6
விடை :
(3) 6

Question 3.
î + ĵ – k̂ மற்றும் \(\vec{i}-2 \vec{j}+\vec{k}\) ஆகிய வெக்டர்களின் கூடுதலுக்கு இணையாக உள்ள அலகு வெக்டர்
(1) \(\frac{\hat{i}-\hat{j}+\hat{k}}{\sqrt{5}}\)
(2) \(\frac{2 \hat{i}+\hat{j}}{\sqrt{5}}\)
(3) \(\frac{2 \hat{i}-\hat{j}+\hat{k}}{\sqrt{5}}\)
(4) \(\frac{2 \hat{i}-\hat{j}}{\sqrt{5}}\)
குறிப்பு:
(î + ĵ – k̂) + (î – 2ĵ – k̂) = 2î – ĵ
எண்ணளவு = \(\sqrt{2^{2}+(-1)^{2}}=\sqrt{5}\)
∴ தேவையான அலகு வெக்டர் = \(\frac{2 \hat{i}-\hat{j}}{\sqrt{5}}\)
விடை :
(4) \(\frac{2 \hat{i}-\hat{j}}{\sqrt{5}}\)

Question 4.
ஒரு வெக்டர் \(\overrightarrow{\mathrm{OP}}\) ஆனது x மற்றும் y அச்சுகளின் மிகைத் திசையில் முறையே 60° மற்றும் 45°-ஐ ஏற்படுத்துகின்றது. \(\overrightarrow{\mathrm{OP}}\) ஆனது -அச்சுடன் ஏற்படுத்தும் கோணம்.
(1) 45°
(2) 60°
(3) 90°
(4) 30°
குறிப்பு :
α = 60°, β = 45° என்க.
cos² α + cos² β + cos² γ = 1
⇒ cos² 60° + cos² 45° + cos² γ = 1
⇒ (\(\frac{1}{2}\))² + (\(\frac{1}{\sqrt{2}}\))² + cos² γ= 1
⇒ \(\frac{1}{4}\) + \(\frac{1}{2}\) + cos² γ = 1
⇒ cos² γ = 1 – \(\frac{1}{4}\) – \(\frac{1}{2}\)
⇒ cos² γ = \(\frac{4-1-2}{4}\) = \(\frac{1}{4}\) = (\(\frac{1}{2}\))²
⇒ cos² γ = cos² 60°
∴ γ = 60
விடை :
(2) 60°

Question 5.
\(\overrightarrow{\mathrm{BA}}\) = 3î + 2ĵ + k̂ மற்றும் B-ன் நிலை வெக்டர் î + 3ĵ – k̂ எனில் A-ன் நிலைவெக்டர்.
(1) 4î + 2ĵ + k̂
(2) 4î + 5ĵ
(3) 4î
(4) -4î
குறிப்பு :
\(\overrightarrow{\mathrm{BA}}\) = 3î + 2ĵ + k̂
\(\overrightarrow{\mathrm{OA}}\) – \(\overrightarrow{\mathrm{OB}}\) = 3î + 2ĵ + k̂
\(\overrightarrow{\mathrm{OA}}\) = (3î + 2ĵ + k̂) + \(\overrightarrow{\mathrm{OB}}\)
= (3î + 2ĵ + k̂) + (î + 3ĵ – k̂)
= 4î + 5ĵ
விடை :
(2) 4î + 5ĵ

Question 6.
ஒரு வெக்டர் ஆய அச்சுகளுடன் சமகோணத்தை ஏற்படுத்தினால் அக்கோணம்
(1) \(\cos ^{-1}\left(\frac{1}{3}\right)\)
(2) \(\cos ^{-1}\left(\frac{2}{3}\right)\)
(3) \(\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right)\)
(4) \(\cos ^{-1}\left(\frac{2}{\sqrt{3}}\right)\)
குறிப்பு :
α = β = γ
cos² α + cos² β + cos² γ = 1
cos² α + cos² α + cos² α = 1
⇒ 3 cos² α = 1
⇒ cos² α = \(\frac{1}{3}\)
⇒ cos α = \(\frac{1}{\sqrt{3}}\)
⇒ α = \(\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right)\)
விடை:
(3) \(\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right)\)

Question 7.
\(\vec{a}\) – \(\vec{b}\), \(\vec{b}\) – \(\vec{c}\), \(\vec{c}\) – \(\vec{a}\) ஆகிய வெக்டர்கள்
(1) ஒன்றுக்கொன்று இணையானது
(2) அலகு வெக்டர்கள்
(3) செங்குத்தான வெக்டர்கள்
(4) ஒருதள வெக்டர்கள்
குறிப்பு :
கெழுக்களின் கூடுதல் பூச்சியம்.
(விடை :
(4) ஒருதள வெக்டர்கள்

Question 8.
ABCD ஓர் இணைகரம் எனில், என்பது – \(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{AD}}\) +\(\overrightarrow{\mathrm{CB}}\) +\(\overrightarrow{\mathrm{CD}}\)
(1) 2(\(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{AD}}\))
(2) 4\(\overrightarrow{\mathrm{AC}}\)
(3) 4\(\overrightarrow{\mathrm{BD}}\)
(4) \(\overrightarrow{0}\)

குறிப்பு :
\(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{AD}}\) + \(\overrightarrow{\mathrm{CB}}\) + \(\overrightarrow{\mathrm{CD}}\) = \(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{AD}}\) – \(\overrightarrow{\mathrm{AD}}\) – \(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{0}\)
விடை :
(4) \(\overrightarrow{0}\)

Question 9.
\(\vec{a}\) மற்றும் \(\vec{b}\)-ஐ அடுத்தடுத்த பக்கங்களாக கொண்ட இணைகரம் ABCD-ன் ஒரு மூலைவிட்டம் \(\vec{a}\) + \(\vec{b}\) எனில் மற்றொரு மூலைவிட்டம் \(\overrightarrow{\mathrm{BD}}\) ஆனது.
(1) \(\vec{a}\) – \(\vec{b}\)
(2) \(\vec{b}\) – \(\vec{a}\)
(3) \(\vec{a}\) + \(\vec{b}\)
(4) \(\frac{\vec{a}+\vec{b}}{2}\)
குறிப்பு :

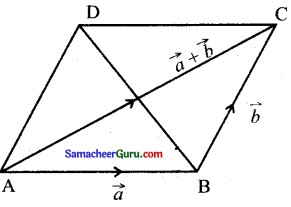
\(\overrightarrow{\mathrm{BD}}\) = \(\overrightarrow{\mathrm{BC}}\) + \(\overrightarrow{\mathrm{CD}}\)
= \(\vec{b}\) + (-\(\vec{a}\))
= \(\vec{b}\) – \(\vec{a}\)
விடை :
(2) \(\vec{b}\) – \(\vec{a}\)

Question 10.
A, B-ன் நிலை வெக்டர்கள் \(\vec{a}\), \(\vec{b}\) எனில், கீழ்க்காணும் நிலை வெக்டர்களில் எந்த நிலை வெக்டரின் புள்ளி A B, என்ற கோட்டின் மீது அமையும்.
(1) \(\vec{a}\) + \(\vec{b}\)
(2) \(\frac{2 \vec{a}-\vec{b}}{2}\)
(3) \(\frac{2 \vec{a}+\vec{b}}{3}\)
(4) \(\frac{\vec{a}-\vec{b}}{3}\)
குறிப்பு :

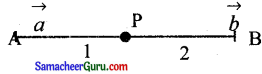
\(\overrightarrow{\mathrm{OP}}\) = \(\frac{1(\vec{b})+2(\vec{a})}{1+2}=\frac{\vec{b}+2 \vec{a}}{3}\)
⇒ \(\overrightarrow{\mathrm{OP}}\) = \(\frac{2 \vec{a}+\vec{b}}{3}\)
விடை :
(3) \(\frac{2 \vec{a}+\vec{b}}{3}\)

Question 11.
\(\vec{a}\), \(\vec{b}\), \(\vec{c}\) ஆகியவை ஒரே கோட்டிலமைந்த மூன்று புள்ளிகளின் நிலைவெக்டர்கள் எனில் கீழ்க்காண்பவைகளுள் எது சரியானது?
(1) \(\vec{a}\) = \(\vec{b}\) + \(\vec{c}\)
(2) 2\(\vec{a}\) = \(\vec{b}\) + \(\vec{c}\)
(3) \(\vec{b}\) = \(\vec{c}\) + \(\vec{a}\)
(4) 4\(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\) = \(\vec{0}\)
குறிப்பு :
மூன்று புள்ளிகளும் ஒரே கோட்டிலமைவன என்பதால்

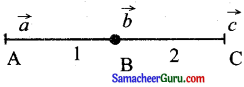
\(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{CA}}\)
⇒ \(\overrightarrow{\mathrm{OB}}\) – \(\overrightarrow{\mathrm{OA}}\) = \(\overrightarrow{\mathrm{OA}}\) – \(\overrightarrow{\mathrm{OC}}\)
⇒ \(\vec{b}\) – \(\vec{a}\) = \(\vec{a}\) – \(\vec{c}\)
⇒ \(\vec{b}\) + \(\vec{c}\) = 2a
(விடை :
(2) 2\(\vec{a}\) = \(\vec{b}\) + \(\vec{c}\)

Question 12.
P என்ற புள்ளியின் நிலை வெக்டர் \(\vec{r}\) = \(\frac{9 \vec{a}+7 \vec{b}}{16}\) என்க P ஆனது \(\vec{a}\) மற்றும் \(\vec{b}\)-ஐ நிலை வெக்டர்களாகக் கொண்ட புள்ளிகளை இணைக்கும் கோட்டைப் பிரிக்கும் விகிதம்
(1) 7 : 9 உட்புறமாக
(2) 9 : 7 உட்புறமாக
(3) 9 : 7 வெளிப்புறமாக
(4) 7 : 9 வெளிப்புறமாக
குறிப்பு:

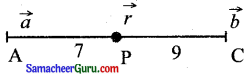
\(\vec{r}\) = \(\frac{9 \vec{a}+7 \vec{b}}{9+7}\)
\(\vec{r}\) = \(\frac{9 \vec{a}+7 \vec{b}}{16}\)
விடை :
(1) 7 : 9 உட்புறமாக்

Question 13.
λî + 2λ ĵ + 2λk̂ என்பது ஓரலகு வெக்டர் எனில், λ-ன் மதிப்பு
(1) \(\frac{1}{3}\)
(2) \(\frac{1}{4}\)
(3) \(\frac{1}{9}\)
(4) \(\frac{1}{2}\)
குறிப்பு :
|λî + 2λ ĵ + 2λk̂| = 1
\(\sqrt{\lambda^{2}+(2 \lambda)^{2}+(2 \lambda)^{2}}\) = 1
⇒ \(\sqrt{9 \lambda^{2}}\) = 1
⇒ 3λ = 1
⇒ λ = \(\frac{1}{3}\)
விடை :
(1) \(\frac{1}{3}\)

Question 14.
ஒரு முக்கோணத்தின் இரண்டு முனைப்புள்ளிகளின் நிலை வெக்டர்கள் 3î + 4ĵ – 4k̂ மற்றும் 2î + 3ĵ + 4k̂. மையக்கோடு சந்தியின் நிலை வெக்டர் î + 2ĵ+ 3k̂ எனில், மூன்றாவது முனைப் புள்ளியின் நிலை வெக்டர்.
(1) -2î – ĵ + 9k̂
(2) -2î – ĵ – 6k̂
(3) 2î – ĵ + 6k̂
(4) -2î + ĵ + 6k̂
குறிப்பு :
\(\overrightarrow{\mathrm{OA}}\) = 3î + 4ĵ – 4k̂
\(\overrightarrow{\mathrm{OB}}\) = 2î + 3ĵ + 4k̂
\(\overrightarrow{\mathrm{OG}}\) = \(\frac{\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}}{3}\)
⇒ 3 \(\overrightarrow{\mathrm{OG}}\) = \(\overrightarrow{\mathrm{OA}}\) + \(\overrightarrow{\mathrm{OB}}\) + \(\overrightarrow{\mathrm{OC}}\)
⇒ 3(î + 2ĵ+ 3k̂) = (3î + 4ĵ – 4k̂) + (2î + 3ĵ + 4k̂)
⇒ \(\overrightarrow{\mathrm{OC}}\) = 3(î + 2ĵ+ 3k̂) – (5î – 7ĵ)
= -2î – ĵ + 9k̂
விடை :
(1) -2î – ĵ + 9k̂

Question 15.
|\(\vec{a}\) + \(\vec{b}\)|= 60, |\(\vec{a}\) – \(\vec{b}\)| = 40 மற்றும் |\(\vec{b}\)| = 46, எனில், |\(\vec{a}\)|-ன் மதிப்பு
(1) 42
2) 12
(3) 22
(4) 32
குறிப்பு :
|\(\vec{a}\) + \(\vec{b}\)|² + |\(\vec{a}\) – \(\vec{b}\)|² = 2[|\(\vec{a}\)|² + |\(\vec{b}\)|²]
60² + 40² = 2[|\(\vec{a}\)|² + 46²]
3600 + 1600 = 2[|\(\vec{a}\)|² + 2116]
|\(\vec{a}\)|²| + 2116 = \(\frac{5200}{2}\) = 2600
|\(\vec{a}\)|²| = 2600 – 2116
|\(\vec{a}\)|²| = 484
|\(\vec{a}\)| = \(\sqrt{484}\) = 22
விடை :
(3) 22

Question 16.
\(\vec{a}\) மற்றும் \(\vec{b}\) ஒரே எண்ணளவைக் கொண்டுள்ளது. இவற்றிற்கு இடைப்பட்ட கோணம் 60° மற்றும் இவற்றின் திசையிலிப் பெருக்கம் \(\frac{1}{2}\) எனில் |\(\vec{a}\)|-என் மதிப்பு
(1) 2
(2) 3
(3) 7
(4) 1
குறிப்பு :
|\(\vec{a}\)| = |\(\vec{b}\)|, θ = 60°, \(\vec{a}\) . \(\vec{b}\) = \(\frac{1}{2}\)
\(\vec{a}\) . \(\vec{b}\) = |\(\vec{a}\)| |\(\vec{b}\)| cos θ
\(\frac{1}{2}\) = |\(\vec{a}\)| |\(\vec{a}\)| cos 60
⇒ \(\frac{1}{2}\) = |\(\vec{a}\)| ² . \(\frac{1}{2}\)
⇒ 1 = |\(\vec{a}\)| ²
∴ |\(\vec{a}\)| = 1
விடை :
(4) 1

Question 17.
\(\vec{a}\) = (sin θ)î + (cos θ)ĵ மற்றும் \(\vec{b}\) = î – √3ĵ + 2k̂ ஆகியவை செங்குத்தாக அமைத்து θ ∈ (0, \(\frac{\pi}{2}\)) எனில், 9-ன் மதிப்பு
(1) \(\frac{\pi}{3}\)
(2) \(\frac{\pi}{6}\)
(3) \(\frac{\pi}{4}\)
(4) \(\frac{\pi}{2}\)
குறிப்பு :
\(\vec{a}\) ⊥ \(\vec{b}\) ⇒ \(\vec{a}\) . \(\vec{b}\) = 0
[sin θî + (cos θ)ĵ] . [î – √3ĵ +2k̂] = 0
⇒ 1(sin θ) – √3 cos θ + 2(0) = 0
sin θ = √3 cos θ
⇒ \(\frac{\sin \theta}{\cos \theta}\) = √3
⇒ tan θ = √3
⇒ θ = \(\frac{\pi}{3}\) = 60°
விடை:
(1) \(\frac{\pi}{3}\)

Question 18.
|\(\vec{a}\)|= 13, |\(\vec{b}\)| = 5 மற்றும் |\(\vec{a}\)| . |\(\vec{b}\)| = 60° எனில், |\(\vec{a}\) × \(\vec{b}\)| -ன் மதிப்பு
(1) 15
(2) 35
(3) 45
(4) 25
குறிப்பு :
|\(\vec{a}\) × \(\vec{b}\)|² + (\(\vec{a}\) . \(\vec{b}\))² = |\(\vec{a}\)|² |\(\vec{b}\)|²
|\(\vec{a}\) \(\vec{a}\)|² + 60² = 13² × 5²
|\(\vec{a}\) \(\vec{a}\)|² = 13 × 13 × 5 × 5 – 3600
|\(\vec{a}\) \(\vec{a}\)|² = 169 × 25 – 3600
= 4225 – 3600 = 625
|\(\vec{a}\) \(\vec{a}\)| = \(\sqrt{625}\) = 25
விடை :
(4) 25

Question 19.
\(\vec{a}\) மற்றும் \(\vec{b}\) ந-க்கு இடைப்பட்ட கோணம் 120° |\(\vec{a}\)| = 1, |\(\vec{b}\)| = 2 எனில், [(\(\vec{a}\) + 3\(\vec{b}\)) × (3\(\vec{a}\) – \(\vec{b}\))]² ன் மதிப்பு
(1) 225
(2) 275
(3) 325
(4) 300
குறிப்பு :
[(\(\vec{a}\) + 3\(\vec{b}\)) × (3\(\vec{a}\) – \(\vec{b}\))]²
= [\(\vec{a}\) × 3\(\vec{a}\) – \(\vec{a}\) × \(\vec{b}\) + 3\(\vec{b}\) × 3\(\vec{a}\) – 3\(\vec{b}\) × \(\vec{b}\)]²
= [0 – \(\vec{a}\) × \(\vec{b}\) – 9\(\vec{a}\) × \(\vec{b}\) – 0]²
= [-10 \(\vec{a}\) × \(\vec{b}\)]²
= 100 |\(\vec{a}\) × \(\vec{b}\)|²
= 100 |\(\vec{a}\)|² |\(\vec{a}\)|² sin² θ
= 100 × (1)² (2)² sin² θ
= 400 sin(180 – 60)² = 400 (sin 60)²
= 400 × (\(\frac{\sqrt{3}}{2}\))² = 400 × \(\frac{3}{4}\) = 300
விடை :
(4) 300

Question 20.
\(\vec{a}\) மற்றும் \(\vec{b}\) ஆகியவற்றின் எண்ண ளவு 2, மேலும் இவற்றிற்கு இடைப்பட்ட கோணம் 60°,எனில், மற்றும் \(\vec{a}\) + \(\vec{b}\) க்கு இடைப்பட்ட கோணம்.
(1) 30°
(2) 60°
(3) 45°
(4) 90°
குறிப்பு :
|\(\vec{a}\) + \(\vec{b}\)| = |\(\vec{a}\)|² + |\(\vec{b}\)|² + 2\(\vec{a}\) . \(\vec{b}\)
= 2² + 2² + 2|\(\vec{a}\)| |\(\vec{b}\)|cos 60°
= 4 + 4 + 2 × 2 × 2 cos 60°
= 8 + 8 × \(\frac{1}{2}\) = 8 + 4 = 12
∴ |\(\vec{a}\) + \(\vec{b}\)| = √12 = 2√3
\(\vec{a}\), \(\vec{a}\) + \(\vec{b}\) இவற்றிற்கு இடைப்பட்ட கோணம் – எனில்
∴
= \(\frac{4+2}{4 \sqrt{3}}=\frac{6}{4 \sqrt{3}}\)
= \(\frac{3}{2 \sqrt{3}}=\frac{\sqrt{3}}{2}\)
⇒ α = 30°
விடை :
(1) 30°

Question 21.
î + 3ĵ + λk̂ ன் மீது 5î – ĵ – 3k̂ ன் விழலும் 5î – ĵ – 3k̂-ன் மீது î + 3ĵ + λk̂ வீழலும் சமம் எனில், λ-ன் மதிப்பு
(1) ±4
(2) ±3
(3) ±5
(4) ±1
குறிப்பு :
\(\vec{a}\) = 5î – ĵ – 3k̂
\(\vec{b}\) = î + 3ĵ + λk̂
\(\vec{c}\) = î + 3ĵ + λk̂
\(\vec{d}\) = 5î – ĵ – 3k̂
\(\vec{b}\) நான் மீது \(\vec{a}\) -என் வீழலும், \(\vec{d}\)-என் மீது \(\vec{c}\)-என் வீழலும் சமம்

விடை :
(3) ±5

Question 22.
î + 5ĵ – 7k̂ என்ற வெக்டரின் ஆரம்ப மற்றும் இறுதிப் புள்ளிகள் (1, 2, 4) மற்றும் (2,-3λ, -3) எனில், λ -ன் மதிப்பு
(1) \(\frac{7}{3}\)
(2) –\(\frac{7}{3}\)
(3) –\(\frac{5}{3}\)
(4) \(\frac{5}{3}\)
குறிப்பு :
\(\overrightarrow{\mathrm{OA}}\) = î + 2ĵ + 4k̂
\(\overrightarrow{\mathrm{OB}}\) = 2î – 3λĵ – 3k̂
\(\overrightarrow{\mathrm{AB}}\) = î + 5ĵ – 7k̂
\(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{OB}}\) – \(\overrightarrow{\mathrm{OA}}\)
î + 5ĵ – 7k̂ = (2î – 3λĵ – 3k̂) – (î + 2ĵ + 4k̂)
î + 5ĵ – 7k̂ = î + (-3λ – 2)ĵ – 7k̂
-(3λ + 2) = 5
3λ + 2 = -5
3λ = -5 – 2 = -7
λ = –\(\frac{7}{3}\)
விடை :
(2) –\(\frac{7}{3}\)

Question 23.
10î + 3ĵ, 12î – 5ĵ மற்றும் aî + 11ĵ ஆகிய நிலை வெக்டர்களின் புள்ளிகள் ஒரே கோட்டில் அமைத்தால் ‘வான் மதிப்பு
(1) 6
(2) 3
(3) 5
(4) 8
குறிப்பு :
\(\overrightarrow{\mathrm{OA}}\) = 10î + 3ĵ
\(\overrightarrow{\mathrm{OB}}\) = 12î – 5ĵ
latex]\overrightarrow{\mathrm{OC}}[/latex] = aî + 11ĵ
\(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{OB}}\) – \(\overrightarrow{\mathrm{OA}}\)
= (12î – 5ĵ) – (10î + 3ĵ) = 2î – 8ĵ

\(\overrightarrow{\mathrm{BC}}\) = \(\overrightarrow{\mathrm{OC}}\) – \(\overrightarrow{\mathrm{OB}}\)
= aî + 11ĵ – (-12î – 5ĵ)
= (a – 12)î + 16ĵ

\(\overrightarrow{\mathrm{CA}}\) = \(\overrightarrow{\mathrm{OA}}\) – \(\overrightarrow{\mathrm{OC}}\)
= (10î + 3ĵ) – (aî + 11ĵ) = (10 – a)î + (-8)ĵ
\(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{CA}}\)
⇒ 2î – 8ĵ = (10 – a)î + (-8)ĵ
(10 – a) = 2
⇒ -a = -10 + 2 = -8
a = 8
விடை :
(4) 8

Question 24.
\(\vec{a}\) = î + ĵ + k̂, \(\vec{b}\) = 2î + xĵ + k̂, \(\vec{c}\) = î – ĵ + 4k̂ மற்றும் a \(\vec{a}\)(\(\vec{b}\) \(\vec{c}\)) = 70 எனில், x-ன் மதிப்பு
(1) 5
(2) 7
(3) 26
(4) 10
குறிப்பு :
\(\vec{a}\) = î + ĵ + k̂
\(\vec{b}\) = 2î + xĵ + k̂
\(\vec{c}\) = î – ĵ + 4k̂
\(\vec{b}\) × \(\vec{b}\) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & x & 1 \\
1 & -1 & 4
\end{array}\right|\)
= î(4x + 1) – ĵ(8 – 1) + k̂(-2 – x)
\(\vec{a}\) . (\(\vec{b}\) × \(\vec{c}\)) = 70
(î + ĵ + k̂) . (î(4x + 1) – ĵ(8 – 1) + k̂(-2 – x)) = 70
(4x + 1) – 7 – 2 – x = 70
3x – 8 = 70
3x = 70 + 8 = 78
x = 26
விடை :
(3) 26

Question 25.
\(\vec{a}\) = î + 2ĵ + 2k̂, |\(\vec{b}\)| = 5 மேலும் \(\vec{a}\) மற்றும் \(\vec{b}\) நாக்கு இடைப்பட்ட கோணம் – எனில், இவ்விரு வெக்டர்களை அடுத்தடுத்த பக்கங்களாகக் கொண்ட முக்கோணத்தின் பரப்பு
(1) \(\frac{7}{4}\)
(2) \(\frac{15}{4}\)
(3) \(\frac{3}{4}\)
(4) \(\frac{17}{4}\)
குறிப்பு :
\(\vec{a}\) = î + 2ĵ + 2k̂, |\(\vec{b}\)| = 5
\(\vec{a}\), \(\vec{b}\)இவற்றிற்கு இடைப்பட்ட கோணம் θ = \(\frac{\pi}{6}\)
|\(\vec{a}\)| = \(\sqrt{1^{2}+2^{2}+2^{2}}=\sqrt{9}=3\)
∆-பின் பரப்பு = \(\frac{1}{2}\) |\(\vec{a}\) × \(\vec{b}\)|
= \(\frac{1}{2}\) |\(\vec{a}\)| |\(\vec{b}\)| sin θ
= \(\frac{1}{2}\) × 3 × 5 sin \(\frac{\pi}{6}\)
= \(\frac{15}{2}\) × \(\frac{1}{2}\) = \(\frac{15}{4}\)
வடை:
(2) \(\frac{15}{4}\)