Samacheer Kalvi 11th Maths Guide Chapter 9 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 9.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 9 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 9.2 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 9 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 9.2

பின்வரும் எல்லை மதிப்புகளைக் காண்க.

Question 1.
\(\lim _{x \rightarrow 2} \frac{x^{4}-16}{x-2}\)
தீர்வு :
\(\lim _{x \rightarrow 2} \frac{x^{4}-16}{x-2}\) = \(\lim _{x \rightarrow 2} \frac{x^{4}-2^{4}}{x-2}\)
[∵ \(\lim _{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}=n \cdot a^{n-1}\)]
= 4(2)^{4 – 1} = 4 × 2³ = 4(8) = 32

Question 2.
\(\lim _{x \rightarrow 1} \frac{x^{m}-1}{x^{n}-1}\), m, n முழு எண்கள.
தீர்வு :
\(\lim _{x \rightarrow 1} \frac{x^{m}-1^{m}}{x^{n}-1^{n}}\)
தொகுதி, பகுதியை (x – 1) ஆல் பெருக்க

Question 3.
\(\lim _{\sqrt{x} \rightarrow 3} \frac{x^{2}-81}{\sqrt{x-3}}\)
தீர்வு :
\(\lim _{\sqrt{x} \rightarrow 3} \frac{x^{2}-81}{\sqrt{x-3}}\) = \(\lim _{\sqrt{x \rightarrow 3}} \frac{x^{2}-9^{2}}{\sqrt{x}-3}\)
= \(\lim _{\sqrt{x} \rightarrow 3} \frac{\left(\sqrt{x}^{2}\right)^{2}-\left(3^{2}\right)^{2}}{\sqrt{x}-3}\)
= \(\lim _{\sqrt{x} \rightarrow 3} \frac{(\sqrt{x})^{4}-3^{4}}{\sqrt{x}-3}\)
= 4 × 3^{4 – 1} = 4 × 3³ = 4 × 27 = 108

Question 4.
\(\lim _{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h}, x>0\)
தீர்வு :
\(\lim _{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h}, x>0\)
தொகுதி, பகுதியை \(\sqrt{x+h}+\sqrt{x}\) ஆல் பெருக்க,

Question 5.
\(\lim _{x \rightarrow 5} \frac{\sqrt{x+4}-3}{x-5}\)
தீர்வு :
\(\lim _{x \rightarrow 5} \frac{\sqrt{x+4}-3}{x-5}\)
தொகுதி, பகுதியை \(\sqrt{x+4}+3\) ஆல் பெருக்க,

Question 6.
\(\lim _{x \rightarrow 2} \frac{\frac{1}{x}-\frac{1}{2}}{x-2}\)
தீர்வு :
\(\lim _{x \rightarrow 2} \frac{\frac{1}{x}-\frac{1}{2}}{x-2}\) = \(\lim _{x \rightarrow 2} \frac{\frac{2-x}{2 x}}{x-2}\)
=
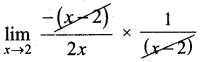
= \(\lim _{x \rightarrow 2} \frac{-1}{2 x}=\frac{-1}{2 \times 2}=-\frac{1}{4}\)

Question 7.
\(\lim _{x \rightarrow 1} \frac{\sqrt{x}-x^{2}}{1-\sqrt{x}}\)
தீர்வு :
\(\lim _{x \rightarrow 1} \frac{\sqrt{x}-x^{2}}{1-\sqrt{x}}=\lim _{x \rightarrow 1} \frac{\sqrt{x}\left(1^{3}-(\sqrt{x})^{3}\right)}{(1-\sqrt{x})}\)
[∵ x² = (√x)⁴ = √x . (√x)³]
=
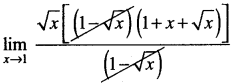
[∵ a³ – b³ = (a – b)(a² + ab + b²]
= \(\lim _{x \rightarrow 1}\) √x(1 + x + √x)
= √1(1 + 1 + √1) = 3

Question 8.
\(\lim _{x \rightarrow 0} \frac{\sqrt{x^{2}+1}-1}{\sqrt{x^{2}+16}-4}\)
தீர்வு :
\(\lim _{x \rightarrow 0} \frac{\sqrt{x^{2}+1}-1}{\sqrt{x^{2}+16}-4}\) = \(\lim _{x \rightarrow 0} \frac{\left(x^{2}+1\right)^{\frac{1}{2}}-1^{\frac{1}{2}}}{\left(x^{2}+16\right)^{\frac{1}{2}}-(16)^{\frac{1}{2}}}\)

தொகுதி, பகுதியை x² ஆல் பெருக்க
= \(\lim _{x \rightarrow 0} \frac{\left(x^{2}+1\right)^{\frac{1}{2}}-1^{\frac{1}{2}}}{x^{2}} \times \frac{x^{2}}{\left(x^{2}+16\right)^{\frac{1}{2}}-16^{\frac{1}{2}}}\)

= \(\lim _{x \rightarrow 0} \frac{\left(x^{2}+1\right)^{\frac{1}{2}}-1^{\frac{1}{2}}}{\left(x^{2}+1\right)-1} \times \frac{\left(x^{2}+16\right)-16}{\left(x^{2}+16\right)^{\frac{1}{2}}-16^{\frac{1}{2}}}\)

Question 9.
\(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x}\)
தீர்வு :
\(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x}\)
தொகுதி, பகுதியை \((\sqrt{1+x}+1)\) ஆல் பெருக்க

Question 10.
\(\lim _{x \rightarrow 1} \frac{\sqrt[3]{7+x^{3}}-\sqrt{3+x^{2}}}{x-1}\)
தீர்வு :

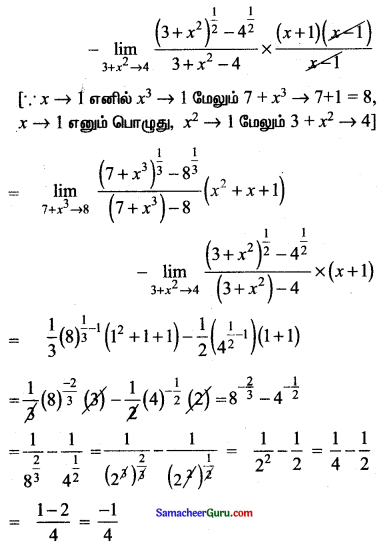
Question 11.
\(\lim _{x \rightarrow 2} \frac{2-\sqrt{x+2}}{\sqrt[3]{2}-\sqrt[3]{4-x}}\)
தீர்வு :

= \(\frac{1}{2} \times(4)^{\frac{1}{2}-1} \times \frac{-1}{\frac{1}{3} \times(2)^{\frac{1}{3}-1}}\)
= \(\frac{1}{2}(4)^{\frac{-1}{2}} \times \frac{-1}{\frac{1}{3}(2)^{-2 / 3}}\)
= –\(\frac{1}{2} \times \frac{3}{1} \times \frac{1}{4^{\frac{1}{2}}} \times 2^{\frac{2}{3}}\)
= \(\frac{-3}{4} \times\left(2^{2}\right)^{\frac{1}{3}}=-\frac{3}{4} \sqrt[3]{4}\)

Question 12.
\(\lim _{x \rightarrow 0} \frac{\sqrt{1+x^{2}}-1}{x}\)
தீர்வு :
\(\lim _{x \rightarrow 0} \frac{\sqrt{1+x^{2}}-1}{x}\)
தொகுதி, பகுதியை \(\left(\sqrt{1+x^{2}}+1\right)\) ஆல் பெருக்க

Question 13.
\(\lim _{x \rightarrow 0} \frac{\sqrt{1-x}-1}{x^{2}}\)
தீர்வு :
\(\lim _{x \rightarrow 0} \frac{\sqrt{1-x}-1}{x^{2}}\)
தொகுதி, பகுதியை \(\sqrt{1-x}+1\) ஆல் பெருக்க

Question 14.
\(\lim _{x \rightarrow 5} \frac{\sqrt{x-1}-2}{x-5}\)
தீர்வு :
\(\lim _{x \rightarrow 5} \frac{\sqrt{x-1}-2}{x-5}\)
தொகுதி, பகுதியை \(\sqrt{x-1}+2\) ஆல் பெருக்க

Question 15.
\(\lim _{x \rightarrow a} \frac{\sqrt{x-b}-\sqrt{a-b}}{x^{2}-a^{2}}(a>b)\)
தீர்வு:
\(\lim _{x \rightarrow a} \frac{\sqrt{x-b}-\sqrt{a-b}}{x^{2}-a^{2}}(a>b)\)
தொகுதி, பகுதியை \(\sqrt{x-b}+\sqrt{a-b}\) ஆல் பெருக்க