Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.2

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.2

Find the derivatives of the following functions with respect to corresponding independent variables.
Question 1.
f(x) = x – 3 sinx
Solution:
f(x) = x – 3 sinx
= f'(x) = 1 – 3 (cos x)
= 1 – 3 cos x

Question 2.
y = sin x + cos x
Solution:
\(\frac{d y}{d x}\) = cosx + (-sinx) = cos x – sin x

Question 3.
f(x) = x sin x
Solution:
f(x) = uv
⇒ f'(x) = uv’ + vu’ = u\(\frac{d u}{d x}\) + v\(\frac{d v}{d x}\)
Now u = x ⇒ u’ = 1
v = sin x ⇒ v’ cos x
f'(x) = x (cos x) + sin x(1)
= x cos x + sin x

Question 4.
y = cos x – 2 tan x
Solution:
\(\frac{d y}{d x}\) = -sin x = 2 (sec²x)
= – sin x – 2 sec²x

Question 5.
g(t) = t³ cos t
Solution:
g(t) = t³ cost (i.e.) u = t³ and v = cos t
let u’ = \(\frac{d u}{d x}\) and v’= \(\frac{d v}{d x}\) = (-sint)
g'(t) = uv’ + vu’
g'(t) = t³ (-sin t) + cos t (3t²)
= -t³ sin t + 3t² cos t

Question 6.
g(t) = 4 sec t + tan t
Solution:
g{t) = 4 sect + tan t
g'(t) = 4(sec t tan t) + sec²t
= 4sec t tan t + sec²t

Question 7.
y = e^x sin x
Solution:
y = e^x sin x
⇒ y = uv’ + vu’
Now u = e^x ⇒ u’ = \(\frac{d u}{d x}\) e^x
v = sin x ⇒ v’ = \(\frac{d v}{d x}\) cos x
i.e. y’ = e^x (cos x) + sin x (e^x)
= e^x [sin x + cos x]

Question 8.
y = \(\frac{\tan x}{x}\)
Solution:

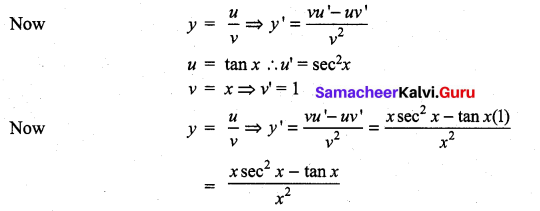
Question 9.
y = \(\frac{\sin x}{1+\cos x}\)
Solution:
y = \(\frac{\sin x}{1+\cos x}=\frac{u}{v}\) (say)
u = sin x v = 1 + cosx
u’ = cos x v’ = -sin x
y = \(\frac{u}{v} \Rightarrow y^{\prime}=\frac{v u^{\prime}-u v^{\prime}}{v^{2}}\)

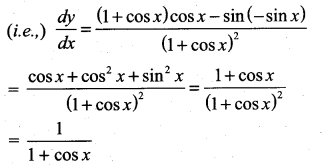
Question 10.
y = \(\frac{x}{\sin x+\cos x}\)
Solution:

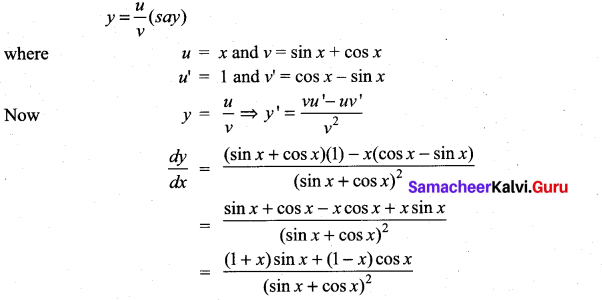
Question 11.
y = \(\frac{\tan x-1}{\sec x}\)
Solution:

Question 12.
y = \(\frac{\sin x}{x^{2}}\)
Solution:

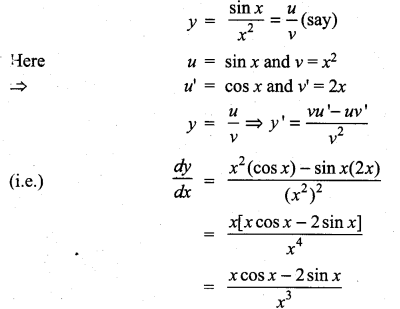
Question 13.
y = tan θ (sin θ + cos θ)
Solution:

Question 14.
y = cosex x. cot x
Solution:
y = u v ⇒ y’ = uv’ + vu’
u = cosec x ⇒ u’ = -cosec x cot x
v = cot x ⇒ v’ = – cosec² x
(cosec x)(-cosec²x) + cot x(-coseç x cot x)
= cosec³x – cosec x cot²x
= – cosec x (cosec²x + cot²x)
= \(-\frac{1}{\sin x}\left(\frac{1+\cos ^{2} x}{\sin ^{2} x}\right)=-\frac{\left(1+\cos ^{2} x\right)}{\sin ^{3} x}\)

Question 15.
y = x sin x cos x
Solution:

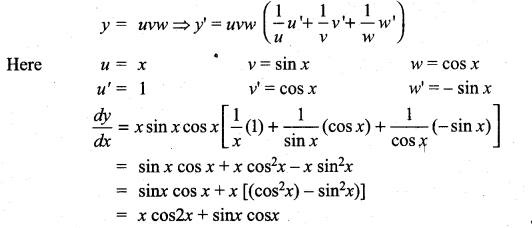
Question 16.
y = e^-x. log x
Solution:
y = e^-x logx = uv (say)
Here u = e^-x and v = log x
⇒ u’ = -e^-x and v’ = \(\frac{1}{x}\)
Now y = uv ⇒ y’ = uv’ + vu’
(i.e.) \(\frac{d y}{d x}\) = e^-x \(\left(\frac{1}{x}\right)\) + log x(-e^-x)
= e^-x(\(\frac{1}{x}\) – log x)

Question 17.
y = (x² + 5) log (1 + x)e^-3x
Solution:

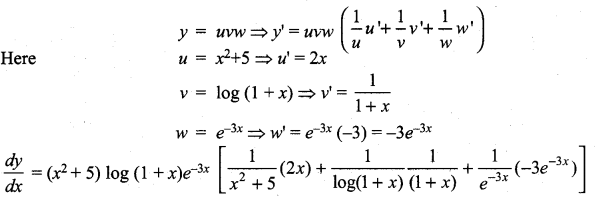
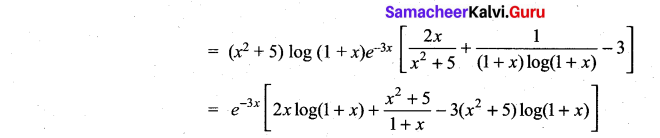
Question 18.
y = sin x⁰
Solution:

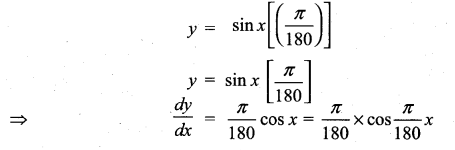
Question 19.
y = log₁₀x
Solution:

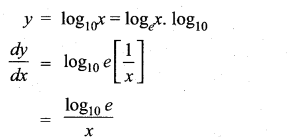
Question 20.
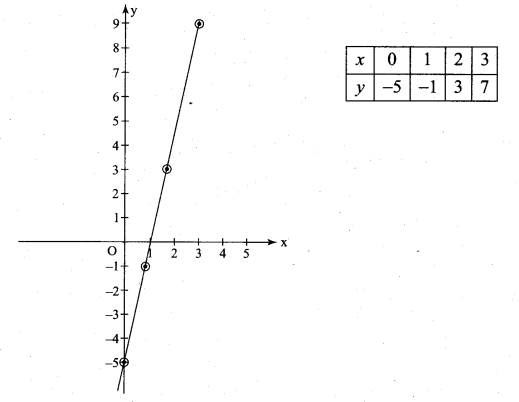
Draw the function f'(x) if f(x) = 2x² – 5x + 3
Solution:
f(x) = 2x² – 5x + 3
f'(x) = 4x – 5 which is a linear function
(i.e.) y = 4x – 5

Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.2 Additional Questions

Question 1.
Find the derivation of following functions
Question 1.
3 sin x + 4 cos x – e^x
Solution:
y = 3 sin x + 4 cos x – e^x
\(\frac{d y}{d x}\) = 3 (cos x) + 4 (- sin x) – (e^x)
= 3 cos x – 4 sin x – e^x

Question 2.
sin 5 + log₁₀x + 2 secx
Solution:
y = sin 5 + log₁₀x + 2 secx
\(\frac{d y}{d x}\) = 0 + \(\left(\frac{1}{x}\right)\) log₁₀ e + 2[sec x + tan x] = \(\frac{\log _{10} e}{x}\) + 2 sec x tan x

Question 3.
6 sin x log₁₀x + e
Solution:

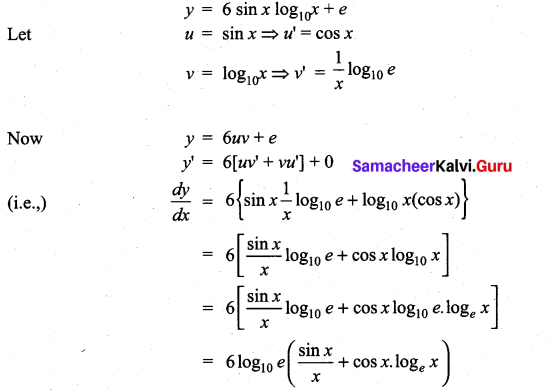
Question 4.
(x⁴ – 6x³ + 7x² + 4x + 2) (x³ – 1)
Solution:
Let u = x⁴ – 6x³ + 7x² + 4x + 2 and v = x³ – 1
u’ = 4x³ – 6 (3x²) + 7 (2x) + 4 (1) + 0
= 4x³ – 18x² + 14x + 4
v’= 3x³
y = uv’ + vu’
i.e. \(\frac{d y}{d x}\) = (x⁴ – 6x³ + 7x² + 4x + 2) (3x²) + (x³ – 1) (4x³ – 18x² + 14x + 4)
= 3x⁶ – 18x⁵ + 21x⁴ + 12x³ + 6x² + 4x⁶ – 18x⁵ + 14x⁴ + 4x³ – 4x³ + 18x² – 14x – 4
= 7x⁶ – 36x⁵ + 35x⁴ + 12x³ + 24x² – 14x – 4

Question 5.
(3x² + 1)²
Solution:
y = (3x² + 1)² = (3x² + 1) (3x² + 1)
Let u = 3x² + 1 and v = 3x² + 1
∴ u’ = 3(2x) = 6x and v’ = 6x
y’ = uv’ + vu’
(i.e.,) \(\frac{d y}{d x}\) = (3x² + 1) (6x) + (3x² + 1) 6x = 12x (3x² + 1)

Question 6.
(3 sec x – 4 cosec x) (2 sin x + 5 cos x)
Solution:
y = (3 sec x – 4 cosec x) (2 sin x + 5cos x)
Let u = 3 secx-4 cosecx and v = 2 sinx + 5 cosx
u’ = 3 (sec x tan x) – 4 (-cosec x cot x) ; v’ = 2 (cos x) + 5 (- sin x)
u’ = 3 sec x tan x + 4 cosec x cot x); v’ = 2 cos x – 5 sin x .
∴ y’ = uv’ + vu’
So \(\frac{d y}{d x}\) = (3 sec x – 4 cosec x) (2 cos x – 5 sinx) + (2 sin x + 5 cos x) (3 sec x tan x + 4 cosec x cot x) = 6 sec x cos x – 15 sec x sin x – 8 cosec x cos x + 20 cosec x sin x + 6 sinx secx tanx + 8 sinx cosecx cotx+ 15 cosx secx tanx + 20 cos x cosec x cot x
= 6 \(\frac{1}{\cos x}\) cosx – 15 \(\frac{1}{\cos x}\)sin x – 8 \(\frac{1}{\sin x}\) cos x + 20 \(\frac{1}{\sin x}\) sin x + 6 sin x \(\frac{1}{\cos x}\) tan x + 8 sin x \(\frac{1}{\sin x}\) cot x + 15 cos x \(\frac{1}{\cos x}\) tan x + 20 cos x \(\frac{1}{\sin x}\) cot x
= 6 – 15tan x – 8cot x + 20 + 6 tan²x + 8 cot x + 15 tan x + 20cot²x
= 26 + 6 tan²x + 20 cot²x

Question 7.
x² e^x sinx
Solution:
y = x² e^x sin x
Let u = x², v = e^x and w = sinx
u’ = 2x, v’ = e^x and w’ = cos x
y’ = uvw’ + vwu’ + uwv’
= (x² e^x) cos x + (e^x sin x)(2x) + (x² sin x)e^x
= x² e^x cos x + 2xe^x sin x + x² e^x sin x
= xe^x {x cos x + 2 sin x + x sin x}

Question 8.
\(\frac{\cos x+\log x}{x^{2}+e^{x}}\)
Solution:
y = \(\frac{\cos x+\log x}{x^{2}+e^{x}}\)
Let u = cos x + log x and v = x² + e^x
∴ u’ = – sin x + \(\frac{1}{x}\), v’ = 2x + e^x

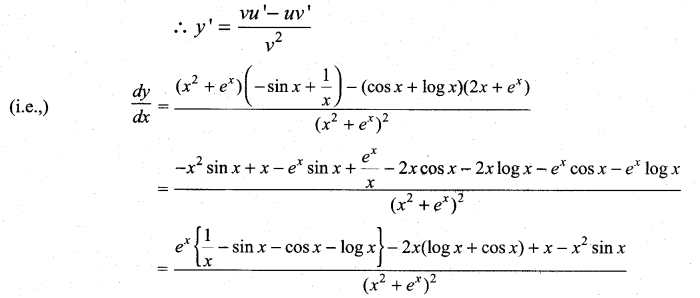
Question 9.
\(\frac{\tan x+1}{\tan x-1}\)
Solution:

Question 10.
\(\frac{\sin x+x \cos x}{x \sin x-\cos x}\)
Solution:
y = \(\frac{\sin x+x \cos x}{x \sin x-\cos x}\)
Let u = sinx + x cosx and v = x sin x – cos x
u’ = cos x + x( – sin x) + cos x (1)
= cos x – x sin x + cos x = 2 cos x – x sin x
v’=x (cos x) + sin x(1) – (- sin x)
= x cos x + sin x + sin x = 2 sin x + x cos x
y = \(\frac{u}{v}\) ∴ y’ = \(\frac{v u^{\prime}-u v^{\prime}}{v^{2}}\)