You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.4
Question 1.
Construct a quadratic equation with roots 7 and -3.
Solution:
The given roots are 7 and -3
Let α = 7 and β = -3
α + β = 7 – 3 = 4
αβ = (7)(-3) = -21
The quadratic equation with roots α and β is x2 – (α + β) x + αβ = 0
So the required quadratic equation is
x2 – (4) x + (-21) = 0
(i.e.,) x2 – 4x – 21 = 0
Question 2.
A quadratic polynomial has one of its zeros 1 + \(\sqrt{5}\) and it satisfies p(1) = 2. Find the quadratic polynomial.
Solution:
Given α = 1 + \(\sqrt{5}\) So, β = 1 – \(\sqrt{5}\)
![]()
The quadratic polynomial is
p(x) = x2 – (α + β)x + αβ
p(x) = k (x2 – 2x – 4)
p( 1) = k(1 – 2 – 4) = -5 k
Given p (1) = 2
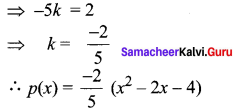
![]()
Question 3.
If α and β are the roots of the quadratic equation x2 + \(\sqrt{2}\)x + 3 = 0, form a quadratic polynomial with zeroes 1/α, 1/β.
Solution:
α and β are the roots of the equation x2 + \(\sqrt{2}\)x + 3 = 0


![]()
Question 4.
If one root of k(x – 1)2 = 5x – 7 is double the other root, show that k = 2 or – 25.
Solution:
k(x – 1)2 = 5x – 7
(i.e.,) k(x2 – 2x + 1) – 5x + 7 = 0
x2 (k) + x(-2k – 5) + k + 1 = 0
kx2 – x(2k + 5) + (k + 7) = 0
Here it is given that one root is double the other.
So let the roots to α and 2α

2(4k2 + 25 + 20k) = 9k (k + 7)
2(4k2 + 25 + 20k) = 9k2 + 63k
8k2 + 50 + 40k – 9k2 – 63k = 0
-k2 – 23k + 50 = 0
k2 + 23k – 5o = 0
(k + 25)(k – 2) = 0
k = -25 or 2
Question 5.
If the difference of the roots of the equation 2x2 – (a + 1)x + a – 1 = 0 is equal to their product then prove that a = 2.
Solution:
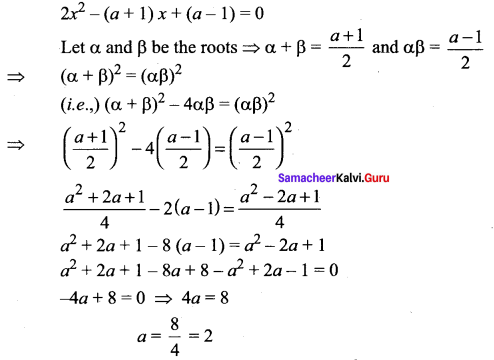
![]()
Question 6.
Find the condition that one of the roots of ax2 + bx + c may be
(i) negative of the other
(ii) thrice the other
(iii) reciprocal of the other.
Solution:
(i) Let the roots be α and -β
Sum of the roots = – b/a = 0 ⇒ b = 0
(ii) Let the roots be α, 3α

Question 7.
If the equations x2 – ax + b = 0 and x2 – ex + f = 0 have one root in common and if the second equation has equal roots that ae = 2(b + f).
Solution:

![]()
Question 8.
Discuss the nature of roots of
(i) -x2 + 3x + 1 = 0
(ii) 4x2 – x – 2 = 0
(iii) 9x2 + 5x = 0
Solution:
(i) -x2 + 3x + 1 = 0
⇒ comparing with ax2 + bx + c = 0
∆ = b2 – 4ac = (3)2 – 4(1)(-1) = 9 + 4 = 13 > 0
⇒ The roots are real and distinct
(ii) 4x2 – x – 2 = 0
a = 4, b = -1, c = -2
∆ = b2 – 4ac = (-1)2 – 4(4)(-2) = 1 + 32 = 33 >0
⇒ The roots are real and distinct
(iii) 9x2 + 5x = 0
a = 9, b = 5, c = 0
∆ = b2 – 4ac = 52 – 4(9)(0) = 25 > 0
⇒ The roots are real and distinct
Question 9.
Without sketching the graphs find whether the graphs of the following functions will intersect the x- axis and if so in how many points.
(i) y = x2 + x + 2
(ii) y = x2 – 3x – 1
(iii) y = x2 + 6x + 9
Solution:


![]()
Question 10.
Write f(x) = x2 + 5x + 4 in completed square form.
Solution:
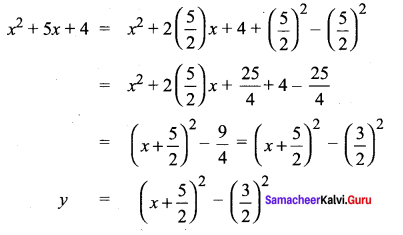
Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.4 Additional Questions
Question 1.
Find the values of k so that the equation x2 = 2x (1 + 3k) + 7(3 + 2k) = 0 has real and equal roots.
Solution:
The equation is x2 – x(2) (1 + 3k) + 7 (3 + 2&) = 0
The roots are real and equal
⇒ ∆ = 0 (i.e.,) b2 – 4ac = 0
Here a = 1, b = -2 (1 + 3k), c = 7(3 + 2k)
So b2 – 4ac = 0 ⇒ [-2 (1 + 3k)]2 – 4(1) (7) (3 + 2k) = 0
(i.e.,) 4 (1 + 3k)2 – 28 (3 + 2k) = 0
(÷ by 4) (1 + 3k)2 – 7(3 + 2k) = 0
1 + 9k2 + 6k – 21 – 14k = 0
9k2 – 8k – 20 = 0
(k – 2)(9k + 10) = 0
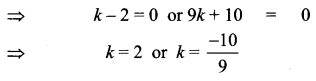
To solve the quadratic inequalities ax2 + bx + c < 0 (or) ax2 + bx + c > 0
![]()
Question 2.
If the sum and product of the roots of the quadratic equation ax2 – 5x + c = 0 are both equal to 10 then find the values of a and c.
Solution:
The given equation is ax2 – 5x + c = 0
Let the roots be α and β Given α + β = 10 and αβ = 10

Question 3.
If α and β are the roots of the equation 3x2 – 4x + 1 = 0, form the equation whose roots are \(\frac{\alpha^{2}}{\beta}\) and \(\frac{\beta^{2}}{\alpha}\)
Solution:


![]()
Question 4.
If one root of the equation 3x2 + kx – 81 = 0 is the square of the other then find k.
Solution:

Question 5.
If one root of the equation 2x2 – ax + 64 = 0 is twice that of the other then find the value of a
Solution:
