You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.2
Question 1.
Express each of the following angles in radian measure:
(i) 30°
(ii) 135°
(iii) -205°
(iv) 150°
(v) 330°
Solution:

Question 2.
Find the degree measure corresponding to the following radian measures
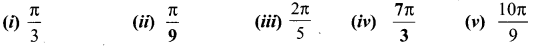
Solution:

![]()
Question 3.
What must be the radius of a circular running path, around which an athlete must run 5 times in order to describe 1 km?
Solution:
Distance travelled in 5 rounds = 1 km = 1000 m
Distance travelled in 1 round = \(\frac{1000}{5}\) = 200 m
Let the radius of the circular path be r metre
So 2πr = 200
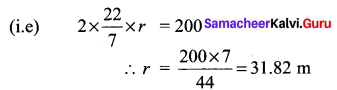
Question 4.
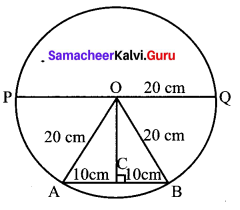
In a circle of diameter 40 cm, a chord is of length 20 cm. Find the length of the minor arc of the chord.
Solution:
O = centre of the circle
PQ = diameter = 40 cm
∴ OQ = 20 cm
radius = 20 cm
⇒ OA = OB = 20 cm
chord AB = 20 cm
OC ⊥ r AB
∴ AC = CB = 10 cm
Now from the right angled triangle OCB
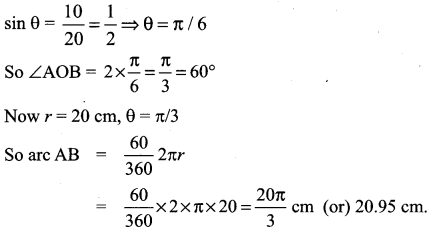
![]()
Question 5.
Find the degree measure of the angle subtended at the centre of circle of radius 100 cm by an arc of length 22 cm.
Solution:
r = 100 cm; arc length = 22 cm

Question 6.
What is the length of the arc intercepted by a central angle of measure 41° in a circle of radius 10 ft?
Solution:
θ = 41°, r = 10 ft

Question 7.
If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Solution:
Let the two radii be r1 and r2
The central angles arc 60° and 75°
The arc lengths be s1 and s2
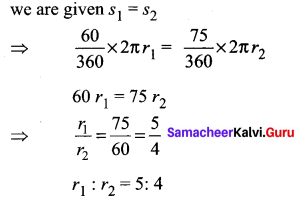
So their radii are in the ratio 5 : 4.
Question 8.
The perimeter of a certain sector of a circle is equal to the length of the arc of a semicircle having the same radius. Express the angle of the sector in degrees, minutes and seconds.
Solution:
Let r be the radius and so perimeter of a sector = l + 2r
Length of arc of the semicircle = πr
we are given l + 2r = πr
(i.e) l = πr – 2r

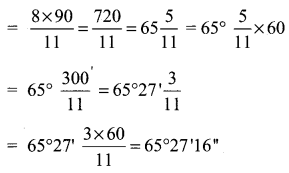
Question 9.
An airplane propeller rotates 1000 times per minute. Find the number of degrees that a point on the edge of the propeller will rotate in 1 second.
Solution:
Number of rotations in 1 min = 1000
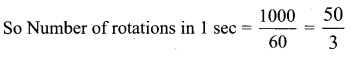
The angle rotated in 1 rotation = 360°
![]()
![]()
Question 10.
A train is moving on a circular track of 1500 m radius at the rate of 66 km / hr. What angle will it turn in 20 seconds?
Solution:
Speed of the train = 66 km/hr

Question 11.
A circular metallic plate of radius 8 cm and thickness 6 mm is melted and molded into a pie (a sector of the circle with thickness) of radius 16 cm and thickness 4 mm. Find the angle of the sector.
Solution:
Area of the circular plate melted
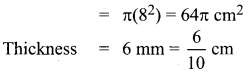

Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.2 Additional Questions
Question 1.
An athlete runs 4 times around a circular running track to describe 1760 m. What is the (radius of the tract) degrees subtended at the centre of the circle, after he has run a distance of 308 m?
Solution:
[Hint: Distance travelled in 4 rounds = 1760 m]

![]()
Question 2.
Find the angle through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 19 cm
Solution:
Here, r = 75 cm

Question 3.
The angles of a quadrilateral are in A.P and the greatest angle is 120°. Express the other angles in radians.
Solution:
Let the angles of the quadrilateral be a°, (a + d)°, (a + 2d)° and (a + 3d)°.
Since sum of all angles of a quadrilateral is 360°, we have .
a° + (a + d)° + (a + 2 d)° + (a + 3 d)° = 360° ⇒ 4a + 6d = 360°
⇒ 2a + 3d = 180° …(1)
Now, greatest angle is 120°
So, a + 3d = 120° …(2)
Solving (1) and (2), we have
a = 60°, d = 20°
Hence, the angles are 60°, 80°, 100°, 120°.
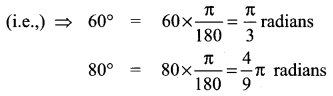
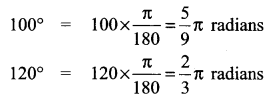
Question 4.
A railroad curve is to be laid out on a circle. What radius should be used if the track is to change direction by 25° in a distance of 40 metres?
Solution:
Let the radius of the circle on which the railroad curve is to be laid down be x metres and the angle subtended by it at the centre is

Question 5.
A horse is tied to a post by a rope. If the horse moves along a circular path always keeping the rope tight and describes 88 metres when it has traced out 72° at the centre, find the length of the rope.
Solution:
Let O be the post.
Let A, B be the two positions of the horse.
Here l, the length of the arc AB = 88 metres
Angle subtended = 72°

Hence, the length of the rope = 70 metres
![]()
Question 6.
A circular wire of radius 3 cm is cut and bent so as to lie along the circumference of a sector whose radius is 48 cm. Find in degrees the angle which is subtended at the centre of the sector.
Solution:
Length of arc = Circumference of wire of radius = 3 cm
l = 2πr = 2π × 3 = 6π cm
The radius of the sector (r) = 48 cm

Question 7.
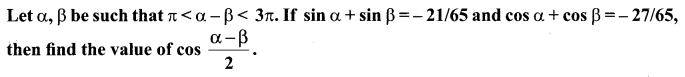
Solution:
