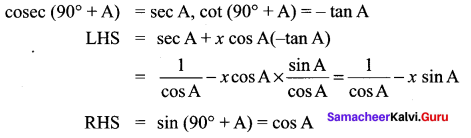Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.3

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.3

Question 1.
Find the values of
(i) sin(480°)
(ii) sin(-1110°)
(iii) cos(300°)
(iv) tan(1050°)
(v) cot(660°)
(vi) tan \(\left(\frac{19 \pi}{3}\right)\)
(vii) sin \(\left(-\frac{11 \pi}{3}\right)\)
Solution:
(i) sin(480°) = sin(360° + 120°) = sin 120°
= sin(90° + 30°) = cos 30° = \(\sqrt{3}\)/2

(ii) sin(-1110°) = -sin(1110°)
= – sin (360° × 3 + 30°)
= -sin 30° = -1/2

(iii) cos(300°) = cos(270° + 30°) = sin 30° = 1/2

(iv) tan(1050°) = tan [3(360°) – 30°]

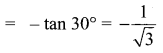
(v) cot(660°) = cot (360° × 2 – 60°)

Question 2.
\(\left(\frac{5}{7}, \frac{2 \sqrt{6}}{7}\right)\) is a point on the terminal side of an angle θ is standard position. Determine the trigonometric function values of angle θ .
Solution:

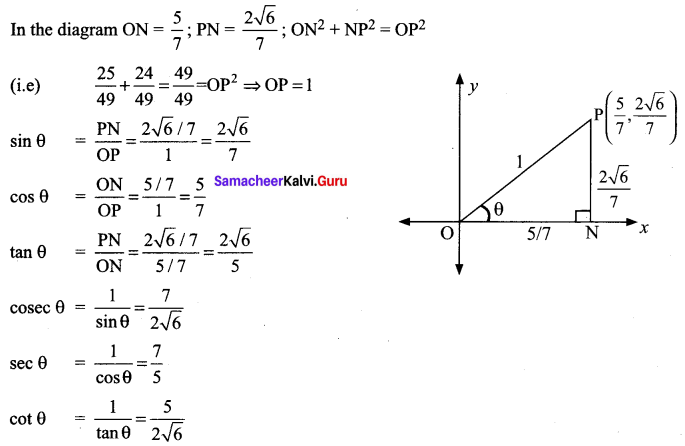
Question 3.
Find the values of other five trigonometric functions for the following:

(i) cos θ = \(-\frac{1}{2}\); θ lies in the III quadrant.
Solution:
Taking the Numerical values

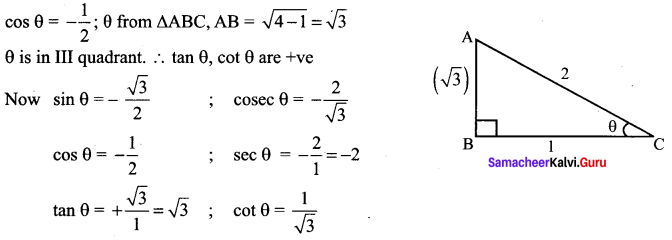
(ii) cos θ = \(\frac{2}{3}\) ; θ lies in the I quadrant
Solution:

(iii) sin θ = –\(\frac{2}{3}\) ; θ lies in the IV quadrant
Solution:

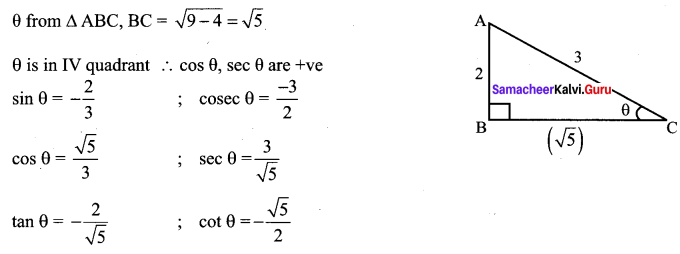
(iv) tan θ = -2; θ lies in the II quadrant
Solution:

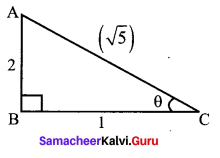
(v) sec θ = \(\frac{13}{5}\) ; θ lies in the IV quadrant
Solution:

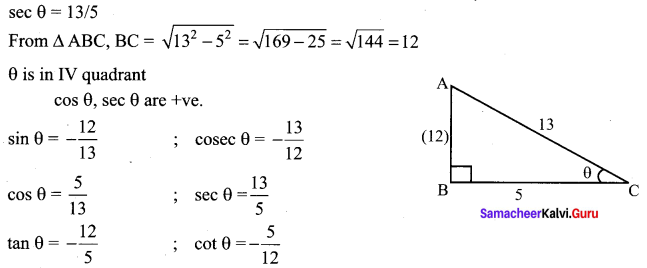
Question 4.

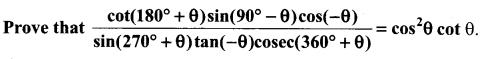
Solution:
cot(180° + θ) = cot θ
sin (90° – θ) = cos θ
cos(-θ) = cos θ
sin (270 + θ) = – cos θ
tan(-θ) = -tan θ
cosec (360° + θ) = cosec θ

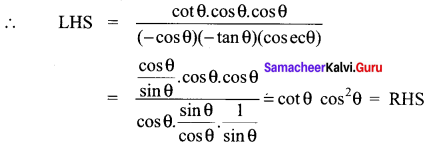
Question 5.
Find all the angles between 0° and 360° which satisfy the equation sin² θ = \(\frac{3}{4}\)
Solution:

Question 6.

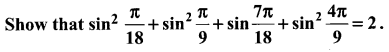
Solution:
LHS = sin² 10° + sin² 20° + sin² 70° + sin² 80°
= sin² 10° + sin² (90° – 10°) + sin² 20° + sin²(90° – 20°)
= sin² 10° + (cos 10°)² + sin² 20° + (cos 20°)²
= (sin² 10+ cos² 10) + sin² 20° + cos² 20°
= 1 + 1 = 2 = RHS

Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.3 Additional Questions Solved

Question 1.
Prove that: sin 600°. tan (-690°) + sec 840°. cot (-945°) = \(\frac{3}{2}\)
Solution:

Question 2.
Prove that sin (270° – θ) sin (90° – θ) – cos (270° – θ) cos (90° + θ) + 1 = 0
Solution:
LHS = sin (270° – θ) sin (90° – θ) – cos (270° – θ) cos (90° + θ) + 1
Now, sin (270° – θ) = sin {180°+ (90°- θ)}
= – cos (90° – θ) = – sin θ
LHS = – cos θ . cos θ – (- sin θ) (- sin θ) + 1
= – cos² θ – sin² θ + 1
= – (cos² θ + sin² θ) + 1 = -1 + 1 = 0 = RHS

Question 3.
Prove that cos 24° + cos 55° + cos 125° + cos 204° + cos 300° = \(\frac{1}{2}\)
Solution:
cos 204° = cos (180°+ 24°) = – cos 24°
cos 125° = cos (180° – 55°) = – cos 55°
LHS = cos 24° + cos 55° + (- cos 55°) + (- cos 24°) + cos 300°
= cos 24° + cos 55° – cos 55° – cos 24° + cos 300°

Question 4.

Solution:

Question 5.

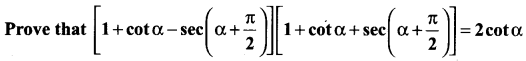
Solution:

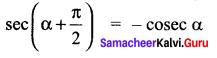
LHS = [(1 +cot α) + cosec α][(1 + cot α) – cosec α]
= (1 + cot α)² – cosec² α
= 1 + cot²α + 2 cot α – cosec² α
[∵ 1 + cot²α = cosec²α]
= cosec²α + 2 cot α – cosec²α
= 2 cot α = RHS

Question 6.

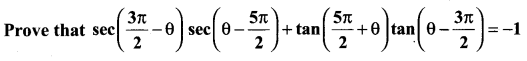
Solution:

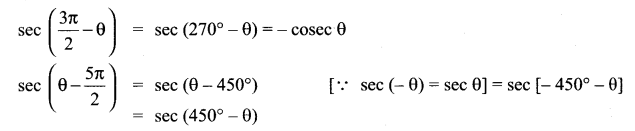
= sec (450° – θ)
= sec[360° + (90° – θ)]
sec (90° – θ) = cosec θ

Question 7.

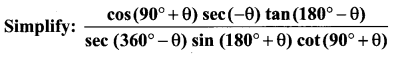
Solution:
cos (90° + θ) = – sin θ
sec (- θ) = sec θ
tan (180° – θ) = – tan θ
sec (360° – θ) = sec θ
sin (180° + θ) = – sin θ
cot (90° + θ) = – tan θ

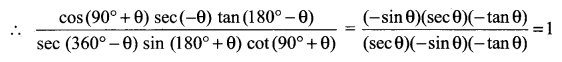
Question 8.
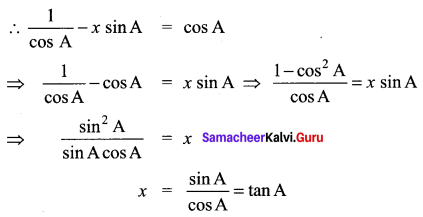
Find x from the equation cosec (90° + A) + x cos A cot (90° + A) = sin (90° + A).
Solution: