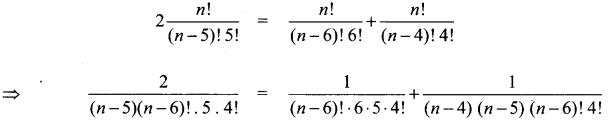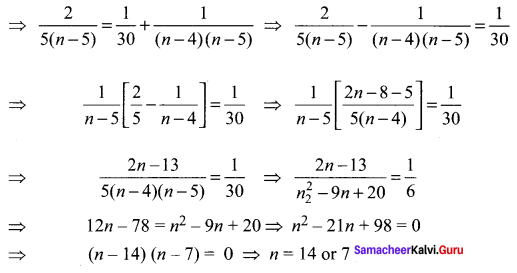Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.3

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.3

Question 1.
If ⁿC₁₂ = ⁿC₉ find ²¹C_n.
Solution:
ⁿC_x = ⁿC_y ⇒ x = y or x + y = n
Here ⁿC₁₂ = ⁿC₉ ⇒ 12 ≠ 9 so 12 + 9 = n (i.e) n = 21

Question 2.
If ¹⁵C_{2r – 1} = ¹⁵C_{2r + 4}, find r.
Solution:

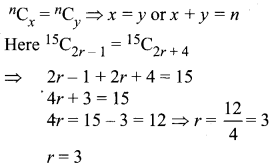
Question 3.
If ⁿP_r = 720 and ⁿC_r = 120, find n, r.
Solution:

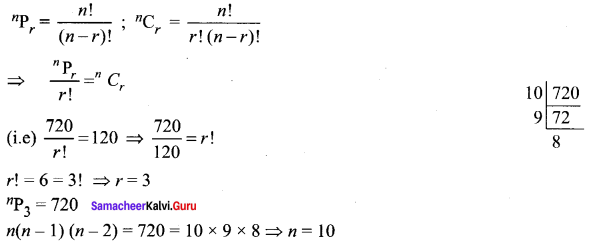
Question 4.
Prove that ¹⁵C₃ + 2 × ¹⁵C₄ + ¹⁵C₅ = ¹⁷C₅
Solution:

Question 5.

Solution:

Question 6.
If ^{(n + 1)}C₈ : ^{(n – 3)}P₄ = 57 : 16, find the value of n.
Solution:

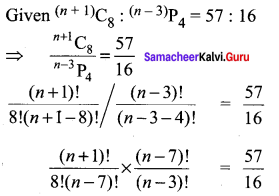
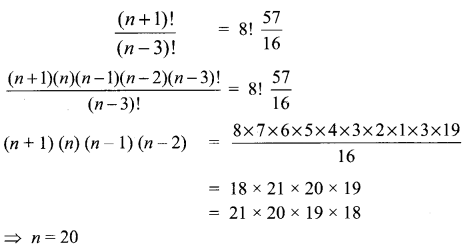
Question 7.

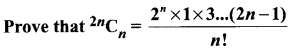
Solution:

Question 8.
Prove that if 1 ≤ r ≤ n then n × ^{(n – 1)}C_{r – 1} = (n – r + 1)C_{r – 1}.
Solution:


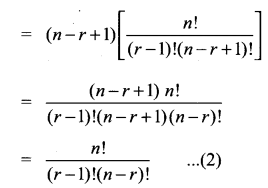
(1) = (2) ⇒ LHS = RHS

Question 9.

(i) A Kabaddi coach has 14 players ready to play. How many different teams of 7 players could the coach put on the court?
Solution:
No. of players in the team = 14
We need 7 players
So selecting 7 from 14 players can be done is ¹⁴C₇ = 3432 ways

(ii) There are 15 persons in a party and if, each 2 of them shakes hands with each other, how many handshakes happen in the party?
Solution:
Total No. of persons = 15
Each two persons shake hands

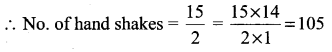
(iii) How many chords can be drawn through 20 points on a circle?
Solution:
A chord is a line join of 2 points
No. of points given = 20
Selecting 2 from 20 can be done in ²⁰C₂ ways

(iv) In a parking lot one hundred, one year old cars are parked. Out of them five are to be chosen at random for to check its pollution devices. How many different set of five cars are possible?
Solution:
Number of cars =100
Select 5 from 100 cars can be done in ¹⁰⁰C₅ ways

(v) How many ways can a team of 3 boys, 2 girls and 1 transgender be selected from 5 boys, 4 girls and 2 transgenders?
Solution:
We have 5 boys, 4 girls and 2 transgenders. We need 3 boys, 2 girls and 1 transgender The selection can be done as follows Selecting 3 boys from 5 boys can be done is ⁵C₃ ways

Selecting 2 girls from 4 girls can be done in ⁴C₂ ways

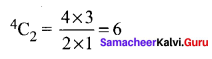
Selecting 1 transgender from 2 can be done in ²C₁ = 2 ways
∴ Selecting 3 boys, 2 girls and 1 transgender can be done in 10 × 6 × 2 = 120 ways

Question 10.
Find the total number of subsets of a set with
(i) 4 elements
(ii) 5 elements
(iii) n elements

Solution:
If a set has n elements then the number of its subsets = 2ⁿ

(i) Here n = 4
So number of subsets = 2⁴ = 16

(ii) n = 5
So number of subsets = 2⁵ = 32

(iii) n = n
So number of subsets = 2

Question 11.
A trust has 25 members.

(i) How many ways 3 officers can be selected?
Solution:
Selecting 3 from 25 can be done in ²⁵C₃ ways

(ii) In how many ways can a President, Vice President and a secretary be selected?
Solution:
From the 25 members a president can be selected in 25 ways
After the president is selected, 24 persons are left out.
So a Vice President can be selected in (from 24 persons) 24 ways.
After the selection of Vice President 23 persons are left out
So a secretary can be selected (from the remaining 23 persons) in 23 ways
So a president, Vice president and a secretary can be selected in ²⁵P₃ ways ²⁵P₃ = 25 × 24 × 23 = 13800 ways

Question 12.
How many ways a committee of six persons from 10 persons can be chosen along with a chair person and a secretary?
Solution:
Selecting a chair person from the 10 persons can be done in 10 ways
After the selection of chair person only 9 persons are left out so selecting a secretary (from the remaining a persons) can be done in 9 ways.
The remaining persons = 8
Totally we need to select 6 persons
We have selected 2 persons.
So we have to select 4 persons
Selecting 4 from 8 can be done in ⁸C₄ ways

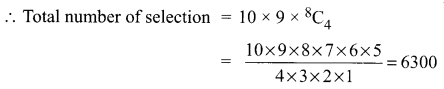
Question 13.
How many different selections of 5 books can be made from 12 different books if,
Solution:
No. of books given = 12
No. of books to be selected = 5

(i) Two particular books are always selected?
Solution:
So we need to select 3 more books from (12 – 2) 10 books which can be done in ¹⁰C₃ ways

(ii) Two particular books are never selected?
Solution:
Two particular books never to be selected.
So only 10 books are there and we have to select 5 books which can be done in ¹⁰C₅ ways

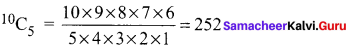
Question 14.
There are 5 teachers and 20 students. Out of them a committee of 2 teachers and 3 students is to be formed. Find the number of ways in which this can be done. Further find in how many of these committees
(i) a particular teacher is included?
(ii) a particular student is excluded?
Solution:
No. of teachers = 5
No of students = 20
We need to select 2 teachers and 3 students

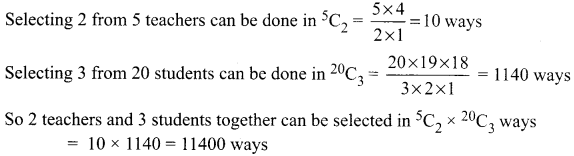
(i) A particular teacher should be included. So from the remaining 4 teachers one teacher is to be selected which can be done in ⁴C₁ = 4 ways

So selecting 2 teachers and 3 students can be done in 4 × 1140 = 4560 ways

(ii) particular student should be excluded.
So we have to select 3 students from 19 students which can be done in ¹⁹C₃ ways

∴ 2 teachers and 3 students can be selected in 969 × 10 = 9690 ways

Question 15.
In an examination a student has to answer 5 questions, out of 9 questions in which 2 are compulsory. In how many ways a students can answer the questions?
Solution:
No. of questions given = 9
No. of questions to be answered = 5
But 2 questions are compulsory
So the student has to answer the remaining 3 questions (5 – 2 = 3) from the remaining 7 (9 – 2 = 7) questions which can be done in ⁷C₃ ways

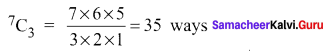
Question 16.
Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly three aces in each combination.
Solution:
No. of cards = 52 : In that number of aces = 4
No. of cards needed = 5
In that 5 cards number of aces needed = 3
So the 3 aces can be selected from 4 aces in ⁴C₃ = ⁴C₁ = 4 ways
So the remaining = 5 – 3 = 2
This 2 cards can be selected in ⁴⁸C₂ ways

Question 17.
Find the number of ways of forming a committee of 5 members out of 7 Indians and 5 Americans, so that always Indians will be the majority’ in the committee.
Solution:
We need a majority of Indian’s which is obtained as follows.

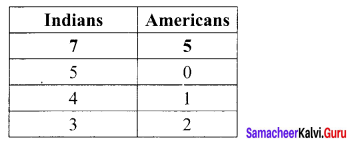
The possible ways are (5I) or (4I and 1A) or (3I and 2A)

Question 18.
A committee of 7 peoples has to be formed from 8 men and 4 women. In how many ways can this be done when the committee consists of
(i) exactly 3 women?
(ii) at least 3 women?
(iii) at most 3 women?
Solution:

We need a committee of 7 people with 3 women and 4 men.
This can be done in (⁴C₃) (⁸C₄) ways

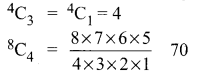
The number of ways = (70) (4) = 280

(ii) Atleast 3 women

So the possible ways are (3W and 4M) or (4W and 3M)

The number of ways (4) (70) + (1) (56) = 280 + 56 = 336

(iii) Atmost 3 women

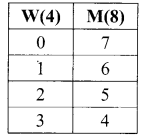
Question 19.
7 relatives of a man comprises 4 ladies and 3 gentlemen, his wife also has 7 relatives; 3 of them are ladies and 4 gentlemen. In how many ways can they invite a dinner party of 3 ladies and 3 gentlemen so that there are 3 of man’s relative and 3 of the wife’s relatives?
Solution:

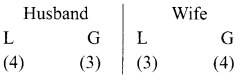
We need 3 ladies and 3 gentlemen for the party which consist of 3 Husbands relative and 3 wifes relative.
This can be done as follows

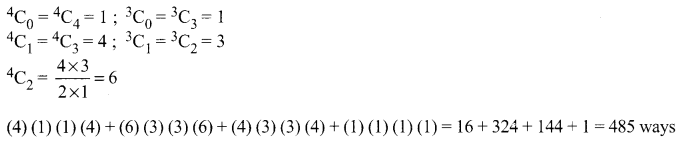
Question 20.
A box contains two white balls, three black balls and four red balls. In how many ways can three balls be drawn from the box, if at least one black ball is to be included in the draw?
Solution:
The box contains 2 white, 3 black and 4 red balls
We have to draw 3 balls in which there should be alteast 1 black ball
The possible draws are as follows
Black balls = 3
Red and White = 2 + 4 = 6

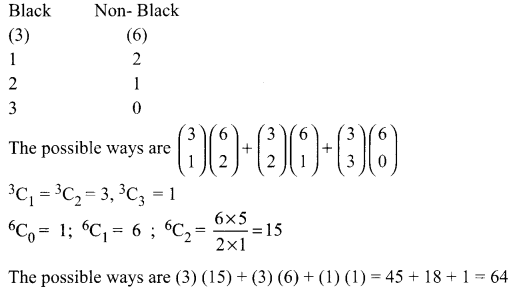
Question 21.
Find the number of strings of 4 letters that can be formed with the letters of the word EXAMINATION.
Solution:
EXAMINATION
(i.e.) A, I, N are repeated twice. So the number of distinct letters = 8
From the 8 letters we have to select and arrange 4 letters to form a 4 letter word which can
be done in ⁸P₄ = 8 × 7 × 6 × 5 = 1680
From the letters A, A, I, I, N, N when any 2 letters are taken as AA, II or AA, NN or II, NN

From AA, II, NN we select one of them and from the remaining we select and arrange 3 which can be done in ways

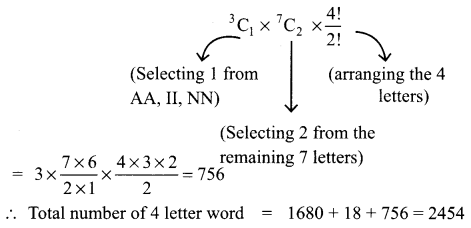
Total number of 4 letter word = 1680 + 18 + 756 = 2454

Question 22.
How many triangles can be formed by joining 15 points on the plane, in which no line joining any three points?
Solution:
No. of non-collinear points = 15
To draw a Triangle we need 3 points
∴ Selecting 3 from 15 points can be done in ¹⁵C₃ ways.

Question 23.
How many triangles can be formed by 15 points, in which 7 of them lie on one line and the remaining 8 on another parallel line?
Solution:

7 points lie on one line and the other 8 points parallel on another paraller line.
A triangle is obtained by taking one point from one line and second points from the other parallel line which can be done as follows.

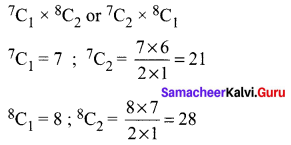
∴ Number of triangles = (7) (28) + (21) (8) = 196 + 168 = 364

Question 24.
There are 11 points in a plane. No three of these lies in the same straight line except 4 points, which are collinear. Find,

(i) The number of straight lines that can be obtained from the pairs of these points?
Solution:
4 points are collinear

Total number of points 11.
To get a line we need 2 points

But in that 4 points are collinear

From (1) Joining the 4 points we get 1 line
∴ Number of lines = ¹¹C₂ – ⁴C₂ + 1 = 55 – 6 + 1 = 50

(ii) The number of triangles that can be formed for which the points as their vertices?
A triangle is obtained by joining 3 points.
So selecting 3 from 11 points can be

But of the 11 points 4 points are collinear. So we have to subtract ⁴C₃ = ⁴C₁ = 4
∴ Number of triangles = 165 – 4 = 161

Question 25.
A polygon has 90 diagonals. Find the number of its sides?
Solution:

∴ n = 15

Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.3 Additional Questions Solved

Question 1.
A group consists of 4 girls and 7 boys. In bow many ways can a team of 5 members be selected, if the team has
(i) no girls
(ii) atleast one boy and one girl.
(iii) at least three girls
Solution:
We have 4 girls and 7 boys and a team of 5 members is to be selected.

(i) If no girl in selected, then all the 5 members are to be selected out of 7 boys

(ii) When at least one boy and one girl are to be selected, then


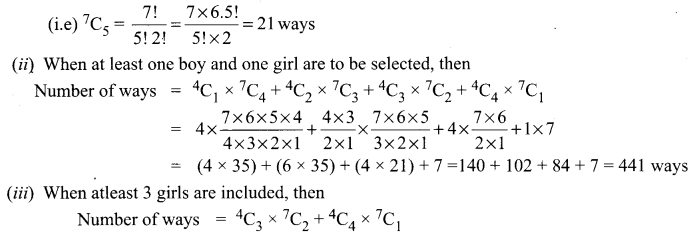
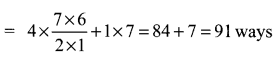
Hence the required number of ways are (i) 21 ways (ii) 441 ways (iii) 91 ways

Question 2.
A committee of 6 is to be choosen from 10 men and 7 women so as to contain atleast 3 men and 2 women. In how many different ways can this be done it two particular women refuse to serve on the same committee?
Solution:
We have 10 men and 7 women out of which a committee of 6 is to be formed which contain atleast 3 men and 2 women

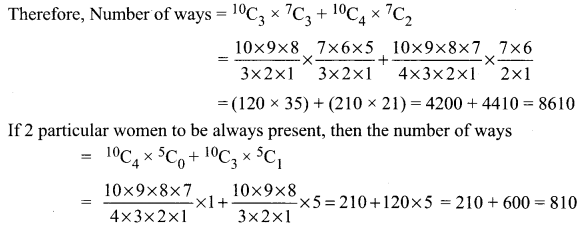
∴ Total number of committee = 8610 – 810 = 7800
Hence, the value of the filler is 7800

Question 3.
Using the digits 1, 2, 3,4, 5, 6, 7 a number of 4 different digits is formed. Find

Solution:
(a) Total of 4 digit number formed with 1, 2, 3, 4, 5, 6, 7

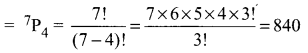
(b) When a number is divisible by 2 = 4 × 5 × 6 × 3 = 360
(c) Total numbers which are divisible by 25 = 40
(d) Total numbers which are divisible by 4 (last two digits is divisble by 4) = 200
Hence, the required matching is (a) ⟷ (z), (b) ⟷ (iii), (c) ⟷ (iv), (d) ⟷ (ii)

Question 4.
If ²²P_{r + 1} : ²⁰P_{r + 2} = 11 : 52, find r.
Solution:

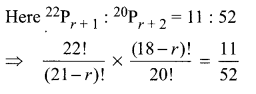
Question 5.

Solution:

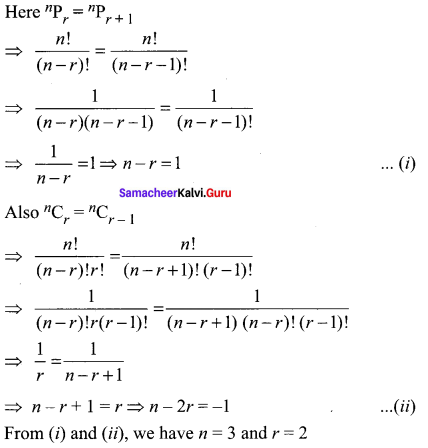
Question 6.
A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of:
(i) exactly 3 girls?
(ii) at least 3 girls?
(iii) almost 3 girls?
Solution:

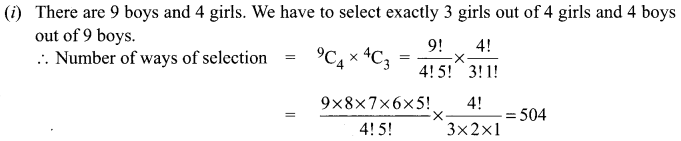
(ii) We have to select at least 3 girls. So the committee consists of 3 girls and 4 boys or 4 girls and 3 boys.
∴ Number of ways of selection = ⁴C₃ × ⁹C₄ + ⁴C₄ × ⁹C₃

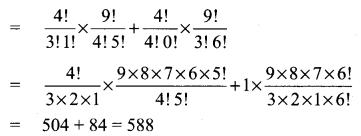
(iii) We have to select at most 3 girls. So the committee consists of no girl and 7 boys or 1 girl and 6 boys or 2 girls and 5 boys or 3 girls and 4 boys.

Question 7.
Determine n if
(i) ²ⁿC₃ : ⁿC₂ = 12 : 1
(ii) ²ⁿC₃ : ⁿC₃ = 11 : 1
Solution:

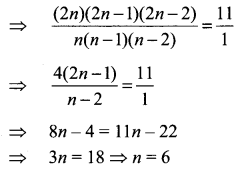
Question 8.
Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.
Solution:
There are 6 red balls, 5 white balls and 5 blue balls.
We have to select 3 balls of each colour.

Question 9.

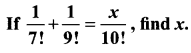
Solution:

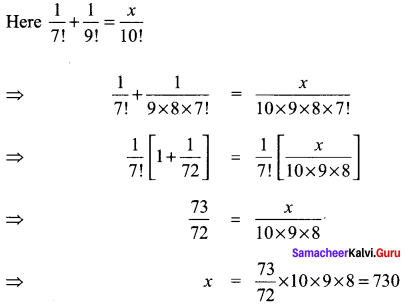
Question 10.
If ⁿC₄, ⁿC₅ and ⁿC₄ are in A.P. then find n.
[Hint: ²ⁿC₅ = ⁿC₆ + ⁿC₄]
Solution: