You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.4
Question 1.
By the principle of mathematical induction, prove that, for n ≥ 1
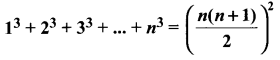
Solution:

∴ P(k+ 1) is true.
Thus P(K) is true ⇒ (k + 1) is true.
Hence by principle of mathematical induction, P(n) is true for all n ∈ N.
Question 2.
By the principle of mathematical induction, prove that, for n > 1
![]()
Solution:
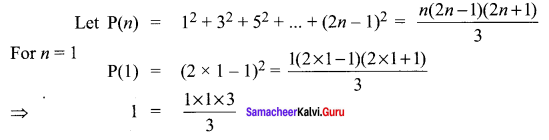
∴ P(1) is true
Let P(n) be true for n = k

∴ P(k + 1) is true
Thus P(k) is true ⇒ P(k + 1) is true. Hence by principle of mathematical induction, P(k) is true for all n ∈ N.
![]()
Question 3.
Prove that the sum of the first n non-zero even numbers is n2 + n.
Solution:
Let P(n) : 2 + 4 + 6 +…+2n = n2 + n, ∀ n ∈ N
Step 1:
P( 1) : 2 = 12 + 1 = 2 which is true for P( 1)
Step 2:
P(k): 2 + 4 + 6+ …+ 2k = k2 + k. Let it be true.
Step 3:
P(k + 1) : 2 + 4 + 6 + … + 2k + (2k + 2)
= k2+ k + (2k + 2) = k2 + 3k + 2
= k2 + 2k + k + 1 + 1
= (k+ 1)2+ (k + 1)
Which is true for P(k + 1)
So, P(k + 1) is true whenever P(k) is true.
Question 4.
By the principle of Mathematical induction, prove that, for n ≥ 1.
![]()
Solution:
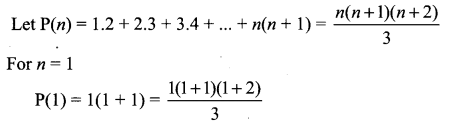

∴ P(k + 1) is true
Thus P(k) is true ⇒ P(k + 1) is true
Hence by principle of mathematical induction, P(n) is true for all n ∈ N
Question 5.
Using the Mathematical induction, show that for any natural number n ≥ 2,
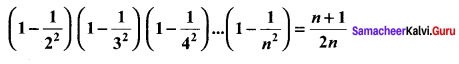
Solution:

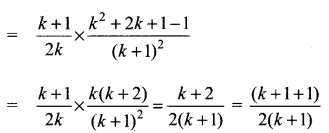
⇒ P(k + 1) is true when P(k) is true so by the principle of mathematical induction P(n) is true.
Question 6.
Using the Mathematical induction, show that for any natural number n ≥ 2,
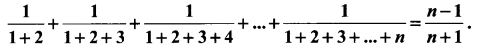
Solution:

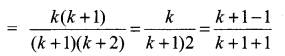
⇒ P(k + 1) is true when P(k) is true so by the principle of mathematical induction P(n) is true for n ≥ 2.
![]()
Question 7.
Using the Mathematical induction, show that for any natural number n
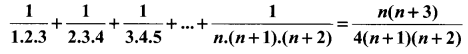
Solution:

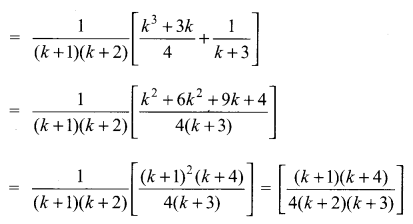
∴ P(k + 1) is true
Thus p(k) is true ⇒ P(k + 1) is true
Hence by principle of mathematical induction,
p(n) is true for all n ∈ z
Question 8.
Using the Mathematical induction, show that for any natural number n,
![]()
Solution:

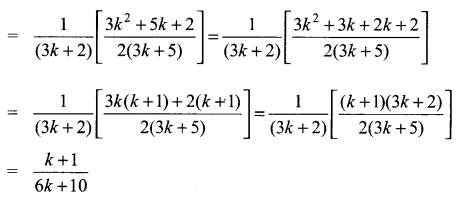
∴ P(k + 1) is true
Thus P(k) is true ⇒ P(k + 1) is true. Hence by principle of mathematical induction, P(n) is true for all n ∈ N.
![]()
Question 9.
Prove by Mathematical Induction that
1! + (2 × 2!) + (3 × 3!) + … + (n × n!) = (n + 1)! – 1
Solution:
P(n) is the statement
1! + (2 × 2!) + (3 × 3!) + ….. + (n × n!) = (n + 1)! – 1
To prove for n = 1
LHS = 1! = 1
RHS = (1 + 1)! – 1 = 2! – 1 = 2 – 1 = 1
LHS = RHS ⇒ P(1) is true
Assume that the given statement is true for n = k
(i.e.) 1! + (2 × 2!) + (3 × 3!) + … + (k × k!) = (k + 1)! – 1 is true
To prove P(k + 1) is true
p(k + 1) = p(k) + t(k + 1)
P(k + 1) = (k + 1)! – 1 + (k + 1) × (k + 1)!
= (k + 1)! + (k + 1) (k + 1)! – 1
= (k + 1)! [1 + k + 1] – 1
= (k + 1)! (k + 2) – 1
= (k + 2)! – 1
= (k + 1 + 1)! – 1
∴ P(k + 1) is true ⇒ P(k) is true, So by the principle of mathematical induction P(n) is true.
Question 10.
Using the Mathematical induction, show that for any natural number n, x2n – y2n is divisible by x +y.
Solution:
Let P(n) = x2n – y2n is divisible by (x + y)
For n = 1
P(1) = x2 × 1 – y2 × 1 is divisible by (x + y)
⇒ (x + y) (x – y) is divisible by (x + y)
∴ P(1) is true
Let P(n) be true for n = k
∴ P(k) = x2k – y2k is divisible by (x + y)
⇒ x2k – y2k = λ(x + y) …… (i)
For n = k + 1
⇒ P(k + 1) = x2(k + 1) – y2(k + 1) is divisible by (x + y)
Now x2(k + 2) – y2(k + 2)
= x2k + 2 – x2ky2 + x2ky2 – y2k + 2
= x2k.x2 – x2ky2 + x2ky2 – y2ky2
= x2k (x2 – y2) + y2λ (x + y) [Using (i)]
⇒ x2k + 2 – y2k + 2 is divisible by (x + y)
∴ P(k + 1) is true.
Thus P(k) is true ⇒ P(k + 1) is true. Hence by principle of mathematical induction, P(n) is true for all n ∈ N
![]()
Question 11.
By the principle of mathematical induction, prove that, for n ≥ 1,
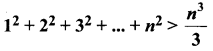
Solution:


Question 12.
Use induction to prove that n3 – 7n + 3, is divisible by 3, for all natural numbers n.
Solution:
Let P(n) : n3 – 7n + 3
Step 1:
P(1) = (1)3 – 7(1) + 3
= 1 – 7 + 3 = -3 which is divisible by 3
So, it is true for P(1).
Step 2:
P(k) : k3 – 7k + 3 = 3λ. Let it be true
⇒ k3 = 3λ + 7k – 3
Step 3:
P(k + 1) = (k + 1)3 – 7(k + 1) + 3
= k3 + 1 + 3k2 + 3k – 7k – 7 + 3
= k3 + 3k2 – 4k – 3
= (3λ + 7k – 3) + 3k2 – 4k – 3 (from Step 2)
= 3k2 + 3k + 3λ – 6
= 3(k2 + k + λ – 2) which is divisible by 3.
So it is true for P(k + 1).
Hence, P(k + 1) is true whenever it is true for P(k).
Question 13.
Use induction to prove that 5n + 1 + 4 × 6n when divided by 20 leaves a remainder 9, for all natural numbers n.
Solution:
P(n) is the statement 5n + 1 + 4 × 6n – 9 is ÷ by 20
P(1) = 51 + 1 + 4 × 61 – 9 = 52 + 24 – 9
= 25 + 24 – 9 = 40 ÷ by 20
So P(1) is true
Assume that the given statement is true for n = k
(i.e) 5k + 1 + 4 × 6n – 9 is ÷ by 20
P(1) = 51 + 1 + 4 × 61 – 9
= 25 + 24 – 9
So P(1) is true
To prove P(k + 1) is true
P(k + 1) = 5k + 1 + 1 + 4 × 6k + 1 + 1 – 9
= 5 × 5 k + 1 + 4 × 6 × 6k – 9
= 5[20C + 9 – 4 × 6k] + 24 × 6k – 9 [from(1)]
= 100C + 45 – 206k + 246k – 9
= 100C + 46k + 36
= 100C + 4(9 + 6k)
Now for k = 1 ⇒ 4(9 + 6k) = 4(9 + 6)
= 4 × 15 = 60 ÷ by 20 .
for k = 2 = 4(9 + 62) = 4 × 45 = 180 ÷ 20
So by the principle of mathematical induction 4(9 + 6k) is ÷ by 20
Now 100C is ÷ by 20.
So 100C + 4(9 + 6k) is ÷ by 20
⇒ P(k + 1) is true whenever P(k) is true. So by the principle of mathematical induction P(n) is true.
![]()
Question 14.
Use induction to prove that 10n + 3 × 4n + 2 + 5, is divisible by 9, for all natural numbers n.
Solution:
P(n) is the statement 10n + 3 × 4n + 2 + 5 is ÷ by 9
P(1) = 101 + 3 × 42 + 5 = 10 + 3 × 16 + 5
= 10 + 48 + 5 = 63 ÷ by 9
So P(1) is true. Assume that P(k) is true
(i.e.) 10k + 3 × 4k + 2 + 5 is ÷ by 9
(i.e.) 10k + 3 × 4k + 2 + 5 = 9C (where C is an integer)
⇒ 10k = 9C – 5 – 3 × 4k + 2 ……(1)
To prove P(k + 1) is true.
Now P(k + 1) = 10k + 1 + 3 × 4k + 3 + 5
= 10 × 10k + 3 × 4k + 2 × 4 + 5
= 10[9C – 5 – 3 × 4k + 2] + 3 × 4k + 2 × 4 + 5
= 10[9C – 5 – 3 × 4k + 2] + 12 × 4k + 2 + 5
= 90C – 50 – 30 × 4k + 2 + 12 × 4k + 2 + 5
= 90C – 45 – 18 × 4k + 2
= 9[10C – 5 – 2 × 4k + 2] which is ÷ by 9
So P(k + 1) is true whenever P(K) is true. So by the principle of mathematical induction P(n) is true.
Question 15.
Prove that using the Mathematical induction
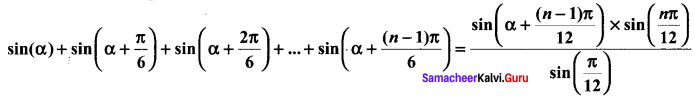
Solution:
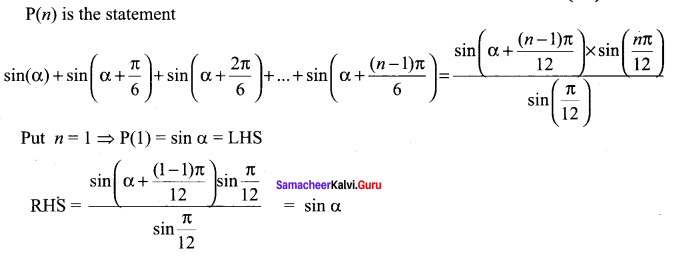

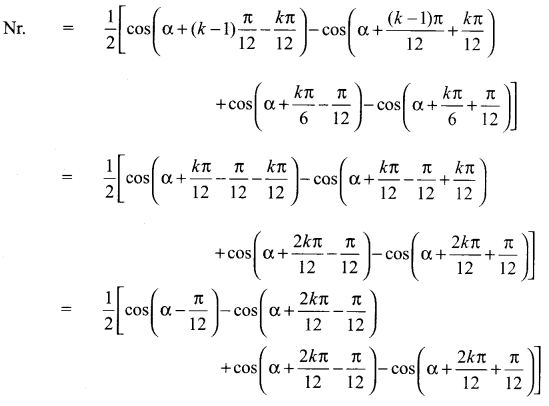

Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.4 Additional Questions
Question 1.
Prove by induction the inequality (1 + x)n ≥ 1 + nx, whenever x is positive and n is a positive integer.
Solution:
P(n) : (1 +x)n ≥ 1 +nx
P(1): (1 + x)1 ≥ 1 + x
⇒ 1 + x ≥ 1 + x, which is true.
Hence, P(1) is true.
Let P(k) be true
(i.e.) (1 + x)k ≥ 1 + kx
We have to prove that P(k + 1) is true.
(i.e.) (1 + x)k + 1 ≥ 1 + (k + 1)x
Now, (1 + x)k + 1 ≥ 1 + kx [∵ p(k) is true]
Multiplying both sides by (1 + x), we get
(1 + x)k(1 + x) ≥ (1 + kx)(1 + x)
⇒ (1 + x)k + 1 ≥ 1 + kx + x + kx2
⇒ (1 + x)k + 1 ≥ 1 + (k + 1)x + kx2 ….. (1)
Now, 1 + (k + 1) x + kx2 ≥ 1 + (k + 1)x …… (2)
[∵ kx2 > 0]
From (1) and (2), we get
(1 + x)k + 1 ≥ 1 + (k + 1)x
∴ P(k + 1) is true if P(k) is true.
Hence, by the principle of mathematical induction, P(n) is true for all values, of n.
Question 2.
32n – 1 is divisible by 8.
Solution:
P(n) = 32n – 1 is divisible by 8
For n = 1, we get
P(1) = 32.1 – 1 = 9 – 1 = 8
P(1) = 8, which is divisible by 8.
Let P(n) be true for n = k
P(k) = 32k – 1 is divisible by 8 ….. (1)
Now, P(k + 1) = 3(2k + 2) – 1 = 32k.32 – 1
= 32(32k – 1) + 8
Now, 32k – 1 is divisible by 9. [Using (1)]
∴ 32 (32k – 1) + 8 is also divisible by 8.
Hence, 32n – 1 is divisible by 8 ∀ n E N
![]()
Question 3.
Prove by the principle of mathematical induction if x and y are any two distinct integers, then xn – yn is divisible by x – y. [OR]
xn – yn is divisible by x – y, where x – y ≠ 0.
Solution:
Let the given statement be P(n).
(i.e.) P(n): xn – yn = M(x – y), x – y ≠ 0
Step I.
When n = 1,
xn – yn = x – y = M(x – y) ….(1)
⇒ P(1) is true.
Step II.
Assume that P(k) is true.
(i.e.) xk – yk = M(x – y), x – y ≠ 0
We shall now show that P(k + 1) is true
Now, xk + 1 – yk + 1 = xk + 1 – xky + xk + 1y – yk + 1
= xk(x – y) + y(xk – yk)
= xk(x – y) + yM(x – y) [Usng ….. (1)]
= (x – y)(xk – yM)
∴ By the principle of mathematical induction, P(n) is true for all n ∈ N
Question 4.
Prove by the principle of mathematical induction that for every natural number n, 32n + 2 – 8n – 9 is divisible by 8.
Solution:
Let P(n): 32n + 2 – 8n – 9 is divisible by 8.
Then, P(1): 32.1 + 2 – 8.1 – 9 is divisible by 8.
(i.e.) 34 – 8 – 9 is divisible by 8 or 81 – 8 – 9 is divisible by 8
(or) 64 is divisible by 8, which is true.
Suppose P(k) is true, then
P(k) : 32k + 2 – 8k – 9 is divisible by 8
(i.e.) 32k + 2 – 8k – 9 = 8m, where m ∈ N (or)
32k + 2 = 8m + 8k + 9
P(k + 1) is the statement given by, …(1)
P(k + 1) : 32(k + 1) + 2 – 8(k + 1) – 9
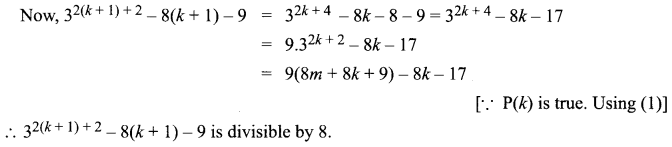
∴ P(k + 1) is true
Hence, by the principle of mathematical induction, P(n) is true for all n ∈ N
Question 5.
Use the principle of mathematical induction to prove that for every natural number n.
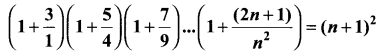
Solution:
Let P(n) be the given statement, i.e.
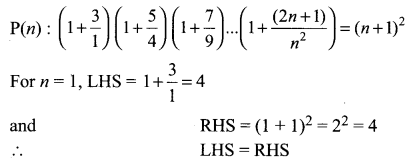
⇒ P(1) is true.
We note than P(n) is true for n = 1.
Assume that P(k) is true
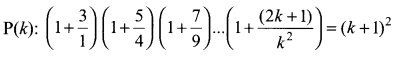
Now, we shall prove that P(k + 1) is true whenever P(k) is true. We have,
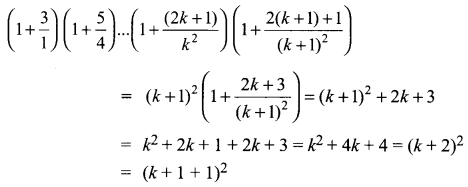
∴ P(k + 1) is also true whenever P(k) is true
Hence, by the principle of mathematical induction, P(n) is also true for all n ∈ N.
Question 6.
n3 – n is divisible by 6, for each natural number n ≥ 2.
Solution:
Let P(n) : n3 – n
Step 1 :
P(2): 23 – 2 = 6 which is divisible by 6. So it is true for P(2).
Step 2 :
P(A): k3 – k = 6λ. Let it is be true for k ≥ 2
⇒ k3 = 6λ + k …(i)
Step 3 :
P(k + 1) = (k + 1)3 – (k + 1)
= k3 + 1 + 3k2 + 3k – k – 1 = k3 – k + 3(k2 + k)
= k3 – k + 3(k2 + k) = 6λ + k – k + 3(k2 + k)
= 6λ + 3(k2 + k) [from (i)]
We know that 3(k2 + k) is divisible by 6 for every value of k ∈ N.
Hence P(k + 1) is true whenever P(k) is true.
![]()
Question 7.
For any natural number n, 7n – 2n is divisible by 5.
Solution:
Let P(n) : 7n – 2n
Step 1 :
P(1) : 71 – 21 = 5λ which is divisible by 5. So it is true for P(1).
Step 2 :
P(k): 7k – 2k = 5λ. Let it be true for P(k)
Step 3 :
P(k + 1) = 7k + 1 – 2k + 1
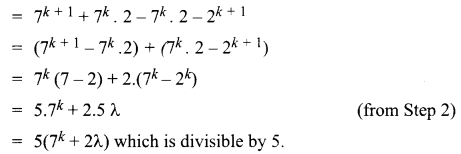
So, it is true for P(k + 1)
Hence, P(k + 1) is true whenever P(k) is true.
Question 8.
n2 < 2n, for all natural numbers n ≥ 5.
Solution:
Let P(n) : n2 < 2n for all natural numbers, n ≥ 5
Step 1 :
P(5) : 15 < 25 ⇒ 1 < 32 which is true for P(5)
Step 2 :
P(k): k2 < 2k. Let it be true for k ∈ N
Step 3 :
P(k + 1): (k + 1)2 < 2k + 1
From Step 2, we get k2 < 2k
⇒ k2 < 2k + 1 < 2k + 2k + 1
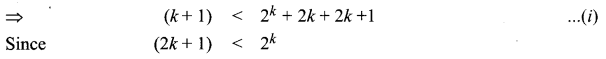
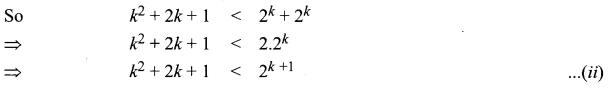
From eqn. (i) and (ii), we get (k + 1)2 < 2k + 1
Hence, P(k + 1) is true whenever P(k) is true for k ∈ N, n ≥ 5.
Question 9.
In 2n < (n + 2)! for all natural number n.
Solution:
Let P(n) : 2n < (n + 2)! for all k ∈ N.
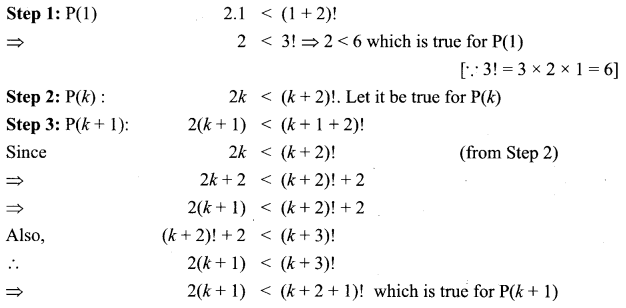
Hence, P(k + 1) is true whenever P(k) is true.
Question 10.
1 + 5 + 9 + … + (4n – 3) = n(2n – 1), ∀ n ∈ N.
Solution:
Let P(n) : 1 + 5 + 9 + … + (4n – 3) = n(2n – 1), ∀ n ∈ N
Step 1:
P(1) : 1 = 1(2.1 – 1) = 1 which is true for P(1)
Step 2:
P(k) : 1 + 5 + 9 + … + (4k – 3) = k(2k – 1). Let it be true.
Step 3:
P(k + 1) : 1 + 5 + 9 + … + (4k – 3) = k(4k + 1)
= k(2k – 1) + (4k + 1) = 2k2 – k + 4k + 1
= 2k2 + 3k + 1 = 2k2 + 2k + k + 1
= 2k(k + 1) + 1 (k + 1) = (2k + 1)(k + 1)
= (k+ 1) (2k + 2 – 1) = (k + 1) [2(k + 1) – 1]
Which is true for P(k + 1).
Hence, P(k + 1) is true whenever P(k) is true.