Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.1

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.1

Question 1.
Find the locus of P, if for all values of a, the co-ordinates of a moving point P is
(i) (9 cos α, 9 sin α)
(ii) (9 cos α, 6 sin α)
Solution:
(i) Let P(h, k) be the moving point.
We are given h = 9 cos α and k = 9 sin α and

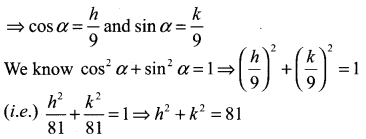
∴ locus of the point is x² + y² = 81

(ii) Let P(h , k) be a moving point.
We are given h = 9 cos α and k = 6 sin α

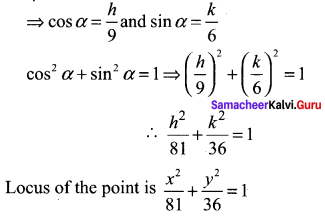
Question 2.
Find the locus of a point P that moves at a constant distant of
(i) Two units from the x-axis
(ii) Three units from the y-axis.
Solution:
(i) Let the point (x, y) be the moving point. Equation of a line at a distance of 2 units from x-axis is k = 2
So the locus is y = 2
(i.e.) y – 2 = 0
435

(ii) Equation of a line at a distance of 3 units from y-axis is h = 3
So the locus is x = 3 (i.e.) x – 3 = 0

Question 3.
If θ is a parameter, find the equation of the locus of a moving point, whose coordinates are x – a cos³ θ, y = a sin³ θ
Solution:

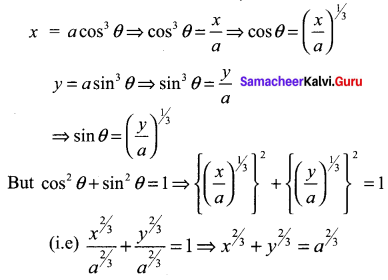
Question 4.
Find the value of k and b, if the points P (-3, 1) and Q (2, b) lie on the locus of x² – 5x + ky = 0.
Solution:
Given P (-3, 1) lie on x² – 5x + ky = 0
⇒ (-3)² – 5(-3) + k(1) = 0
9 + 15 + k = 0 ⇒ k = -24
Q (2, b) lie on x² – 5x + ky = 0
(2)² – 5(2) + k(b) = 0 ⇒ 4 – 5(2) – 24b = 0

Question 5.
A straight rod of length 8 units slides with its ends A and B always on the x and y-axis respectively. Find the locus of the mid point of the line segment AB.
Solution:
Let P (h, k) be the moving point A (a, 0) and B (0, b) P is the mid point of AB.

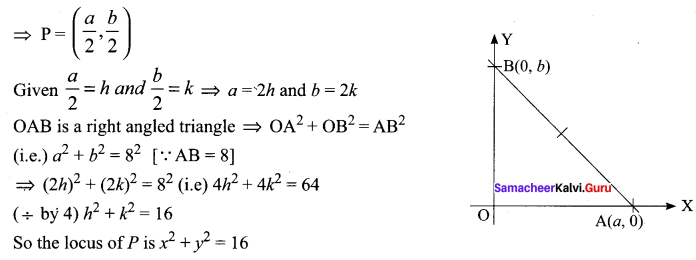
Question 6.
Find the equation of the locus of a point such that the sum of the squares of the distance from the points (3, 5), (1, -1) is equal to 20.
Solution:
Let P (h, k) be the moving point
Let the given point be A (3, 5) and B (1, -1)
We are given PA² + PB² = 20
⇒ (h – 3)² + (k – 5)² + (h – 1)² + (k + 1)² = 20
⇒ h² – 6h + 9 + k² – 10k + 25 + h² – 2h + 1 + k² + 2k + 1 = 20
(i.e.) 2h² + 2k² – 8h – 8k + 36 – 20 = 0
2h² + 2k² – 8h – 8k + 16 = 0
(÷ by 2 ) h² + k² – 4h – 4k + 8 = 0
So the locus of P is x² + y² – 4x – 4y + 8 = 0

Question 7.
Find the equation of the locus of the point P such that the line segment AB, joining the points A (1, -6) and B (4, -2), subtends a right angle at P.
Solution:
Let P (h, k) be the moving point

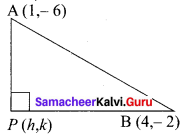
Given A (1, – 6) and B (4, – 2),
Since ∆APB = 90°, PA² + PB² = AB²
(i.e.) (h – 1)² + (k + 6)² + (h – 4)² + (k + 2)² = (4 – 1)² + (-2 + 6)²
(i.e) h² + 1 – 2h + k² + 36 + 12k + h² + 16 – 8h + k² + 4 + 4k = 3² + 4² = 25
2h² + 2k² -10h + 16k + 57 – 25 = 0
2h² + 2k² – 10h + 16k + 32 = 0
(÷ by 2)h² + k² – 5h + 8k + 16 = 0
So the locus of P is x² + y² – 5x + 8y + 16 = 0

Question 8.
If O is origin and R is a variable point on y² = 4x, then find the equation of the locus of the mid-point of the line segment OR.
Solution:
Let P(h, k) be the moving point
We are given O (0, 0). Let R = (a, b)

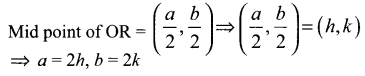
Substituting a, b values is y² = 4x
we get (2k)² = 4 (2h)
(i.e) 4k² = 8h
(÷ by 4) k² = 2h
So the locus of P is y² = 2x

Question 9.

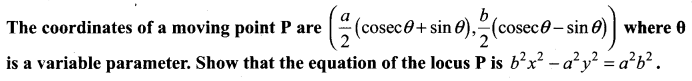
Solution:

Question 10.
If P (2, -7) is a given point and Q is a point on 2x² + 9y² = 18, then find the equations of the locus of the mid-point of PQ.
Solution:
P = (2, -7); Let (h, k) be the moving point Q = (a, b)

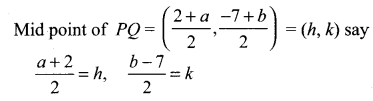
⇒ a = 2h – 2,
b = 2k + l
Q is a point on 2x² + 9y² = 18 (i.e) (a, b) is on 2x² + 9y² = 18
⇒ 2(2h – 2)² + 9 (2k + 7)² = 18
(i.e) 2 [4h² + 4 – 8h] + 9 [4k² + 49 + 28k] – 18 = 0
(i.e) 8h² + 8 – 16h + 36k² + 441 + 252k – 18 = 0
8h² + 36k² – 16h + 252k + 431 = 0
The locus is 8x² + 36y² – 16x + 252y + 431 = 0

Question 11.
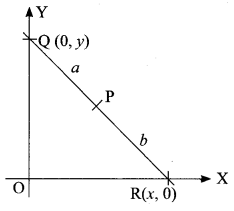
If R is any point on the x-axis and Q is any point on the y-axis and Pis a variable point on RQ with RP = b, PQ = a. then find the equation of locus of P.
Solution:
P = (x, 0), Q = (0, y), R (h, k) be a point on RQ such that PR : RQ = b : a

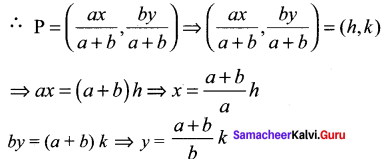
From the right angled triangle OQR, OR² + OQ² = QR²

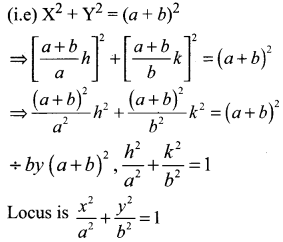
Question 12.
If the points P (6, 2) and Q (-2, 1) and R are the vertices of a ∆PQR and R is the point on the locus y = x² – 3x + 4, then find the equation of the locus of centroid of ∆PQR.
Solution:
P (6, 2), Q (-2, 1). Let R = (a, b) be a point on y = x² – 3x + 4.

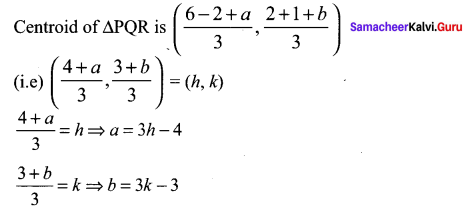
But (a, b) is a point on y = x² – 3x + 4
b = a² – 3a + 4
(i.e) 3k – 3 = (3h – 4)² – 3(3h – 4) + 4
(i.e) 3k – 3 = 9h² + 16 – 24h – 9h + 12 + 4
⇒ 9h² – 24h – 9h + 32 – 3k + 3 = 0
(i.e) 9h² – 33h – 3k + 35 = 0,
Locus of (h, k) is 9x² – 33x – 3y + 35 = 0

Question 13.
If Q is a point on the locus of x² + y² + 4x – 3y + 7 = 0 then find the equation of locus of P which divides segment OQ externally in the ratio 3 : 4, where O is origin.
Solution:
Let (h, k) be the moving point O = (0, 0);
Let PQ = (a, b) on x² + y² + 4x – 3y + 7 = 0

Question 14.
Find the points on the locus of points that are 3 units from x – axis and 5 units from the point (5, 1).
Solution:
A line parallel to x-axis is of the form y = k. Here k = 3 ⇒y = 3
A point on this line is taken as P (a, 3). The distance of P (a, 3) from (5, 1) is given as 5 units
⇒ (a – 5)² + (3 – 1)² = 5²
a² + 25 – 10a + 9 + 1 – 6 = 25
a² – 10a + 25 + 4 – 25 = 0
a² – 10a + 4 = 0

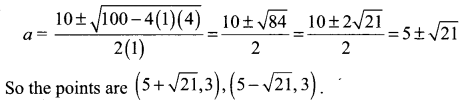
Question 15.
The sum of the distance of a moving point from the points (4, 0) and (-4, 0) is always 10 units. Find the equation of the locus of the moving point.
Solution:
Let P (h, k) be a moving point
Here A = (4, 0) and B = (-4, 0)
Given PA + PB = 10

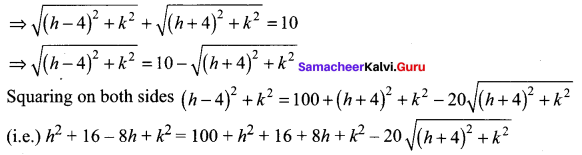
Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.1 Additional Questions

Question 1.
If the sum of the distance of a moving point in a plane from the axis is 1, then find the locus of the point.
Solution:
Let coordinates of a moving point P be (x, y).
Given that the sum of the distances from the axis to the point is always 1.

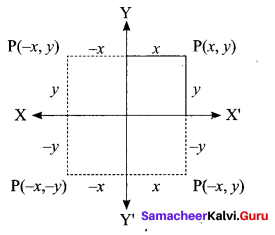
∴ |x| + |y| = 1 ⇒ x + y = 1
⇒ -x – y = 1 ⇒ x – y = 1
Hence, these equations give us the locus of the point P which is a square.

Question 2.
A point moves so that square of its distance from the point (3, -2) is numerically equal to its distance from the line 5x -12y = 3. The equation of its locus is ……..
Solution:
The given equation of line is 5x – 12y = 3 and the given point is (3, -2).
Let (a, b) be any moving point.


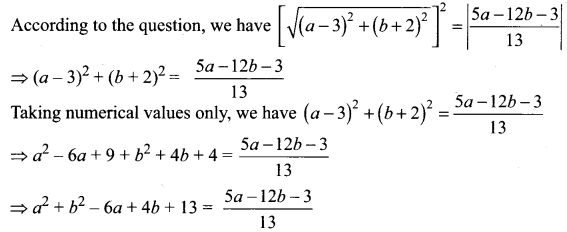
⇒ 13a² + 13b² – 78a + 52b + 169 = 5a – 12b – 3
⇒ 13a² + 13b² – 83a + 64b + 172 = 0
So, the locus of the point is 13x² + 13y² – 83x + 64y + 172 = 0

Question 3.
Find the Locus of the mid points of the portion of the line x cos θ + y sin θ = p intercepted between the axis.
Solution:
Given equation of the line is x cos θ + y sin θ = p … (i)
Let C (h, k) be the mid point of the given line AB where it meets the two axis at A (a, 0) and B (0, b).
Since (a, 0) lies on eq (i) then “a cos θ + θ = p”


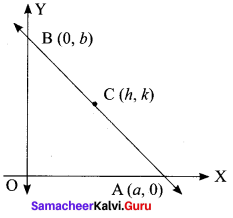
B (0, b) also lies on the eq (i) then 0 + b sin θ = p

Since C (h, k) is the mid point of AB

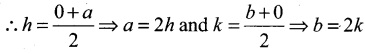
Putting the values of a and b is eq (ii) and (iii) we get P

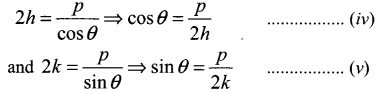
Squaring and adding eq (iv) and (v) we get

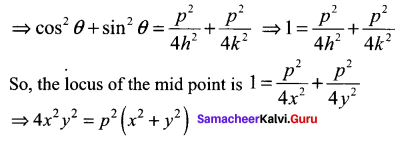
Question 4.

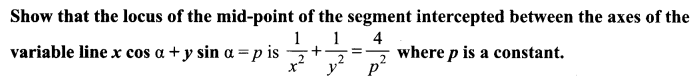
Solution:

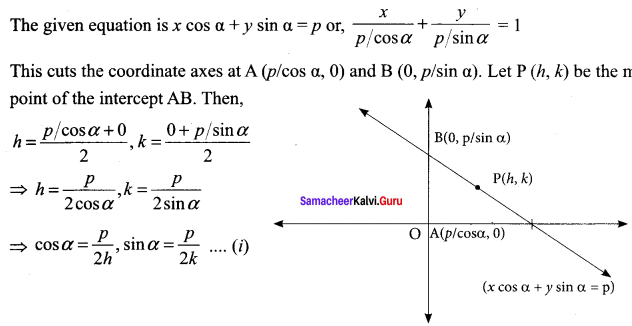
Here, α is a variable. To find the locus of P (h, k), we have to eliminate α.
From (i), we obtain

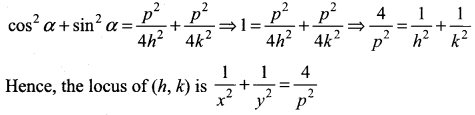
Question 5.

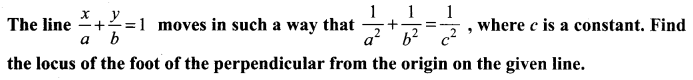
Solution: