You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.2
Question 1.
Find the equation of the lines passing through the point (1, 1)
(i) With y-intercept (- 4)
(ii) With slope 3
(iii) And (-2, 3)
(iv) And the perpendicular from the origin makes an angle 60° with x-axis.
Solution:
(i) Given y intercept = – 4,
Let x intercept be a
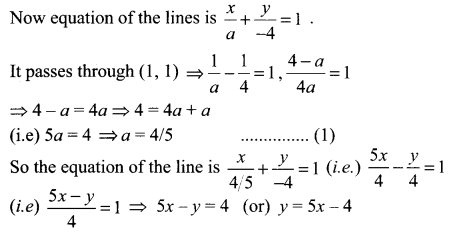
(ii) Slope m = 3, passing through (x1, y1) = (1, 1)
Equation of the line is y – y1 = m(x – x1)
(i.e) y- 1 = 3(x – 1) ⇒ y – 1 = 3x – 3 ⇒ 3x – y = 2
(iii) Passing through (1, 1) and (-2, 3)

![]()
Question 2.
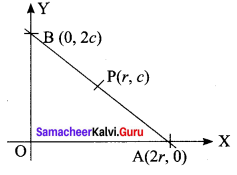
If P (r, c) is mid point of a line segment between the axes, then show that \(\frac{x}{r}+\frac{y}{c}=\) 2.
Solution:
P (r, c) is the mid point of AB.
⇒ A = (2r, 0) and B = (0, 2c)
(i.e) x intercept = 2r and
y intercept = 2c .
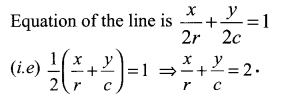
Question 3.
Find the equation of the line passing through the point (1, 5) and also divides the co-ordinate axes in the ratio 3 : 10.
Solution:
Let x intercept be 3a and y intercept be 10a

Question 4.
If p is length of perpendicular from origin to the line whose intercepts on the axes are a and b, then show that \(\frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}\)
Solution:

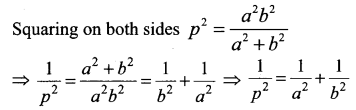
Question 5.
The normal boiling point of water is 100°C or 212°F and the freezing point of water is 0°C or 32°F.
(i) Find the linear relationship between C and F
(ii) Find the value of C for 98.6° F and
(iii) The value of F for 38°C .
Solution:
Given when C = 100, F = 212 and when C = 0, F = 32

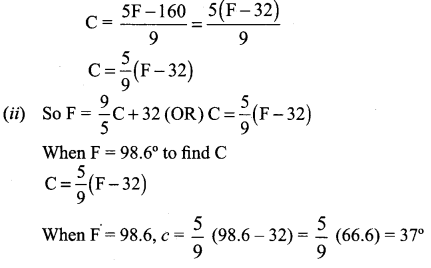
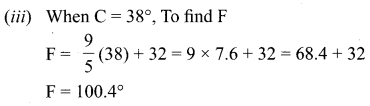
Question 6.
An object was launched from a place P in constant speed to hit a target. At the 15th second it was 1400m away from the target and at the 18th second 800m away. Find
(i) The distance between the place and the target
(ii) The distance covered by it in 15 seconds,
(iii) Time taken to hit the target.
Solution:
Taking time = x and distance = y
We are given at x = 15, y = 1400 and at x = 18, y = 800


![]()
Question 7.
Population of a city in the years 2005 and 2010 are 1,35,000 and 1,45,000 respectively. Find the approximate population in the year 2015. (assuming that the growth of population is constant).
Solution:
Taking year as x and population as y
We are given when x = 2005,
y = 1,35,000 and
when x = 2010,
y = 1,45,000
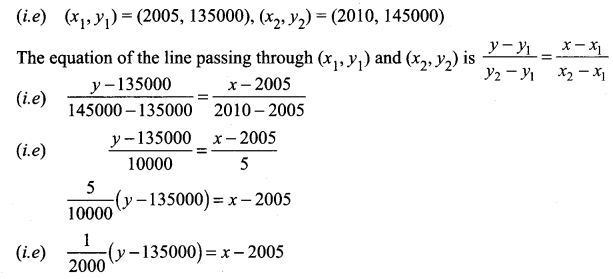
y – 135000 = 2000 (x – 2005)
y = 2000(x – 2005) + 135000
At x = 2015, y = 2000 (2015 – 2005) + 135000
(i.e) y = 2000 (10) + 135000 = 20000 + 135000 = 1,55,000
The approximate population in the year 2015 is 1,55,000
Question 8.
Find the equation of the line, if the perpendicular drawn from the origin makes an angle 30° with x – axis and its length is 12.
Solution:
The equation of the line is x cos α + y sin α = p
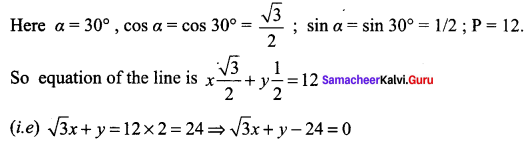
Question 9.
Find the equation of the straight lines passing through (8, 3) and having intercepts whose sum is 1.
Solution:
Given sum of the intercepts = 1 ⇒ when x intercept = a then y intercept = 1 – a
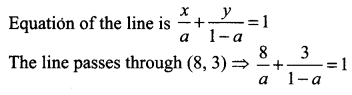
8 (1 – a) + 3a = a (1 – a)
8 – 8a + 3a = a – a2
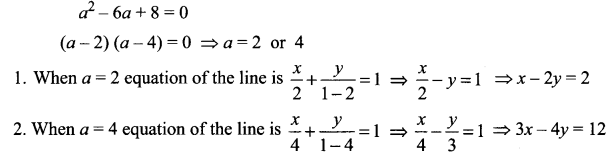
Question 10.
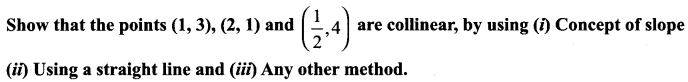
Solution:

⇒ The points A, B, C lie on a line
⇒ The points A, B, C are collinear
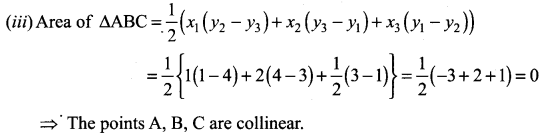
Question 11.
A straight line is passing through the point A (1, 2) with slope \(\frac{5}{12}\). Find points on the line which are 13 units away from A.
Solution:

Question 12.
A 150m long train is moving with constant velocity of 12.5 m/s. Find
(i) The equation of the motion of the train,
(ii) Time taken to cross a pole,
(iii) The time taken to cross the bridge of length 850 m is?
Solution:
(i) Now m = \(\frac{y}{x}\) = 12.5m / second,
The equation of the line is y = mx + c ….(1)
Put c = -150, m = 12.5 m,
The equation of motion of the train is y = 12.5x – 150
(ii) To find the time taken to cross a pole we take y = 0 in (1)
⇒ 0 = 12.5x – 150 ⇒ 12.5x = 150
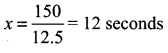
(iii) When y = 850 in (1)
850 = 12.5 x – 150 ⇒ 12.5x = 850 + 150 = 1000
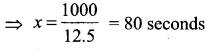
![]()
Question 13.
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time shown in the following table.

(i) Draw a graph showing the results.
(ii) Find the equation relating the length of the spring to the weight on it.
(iii) What is the actual length of the spring.
(iv) If the spring has to stretch to 9 cm long, how much weight should be added?
(v) How long will the spring be when 6 kilograms of weight on it?
Solution:
Taking weight (kg) as x values and length (cm) as y values we get (x1, y1) = (2, 3), (x2, y2) = (4, 4)
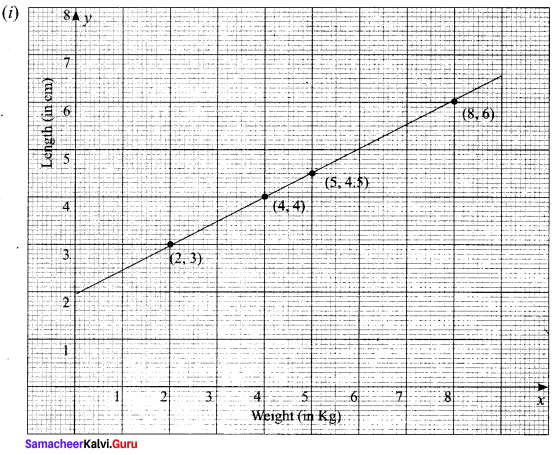
The equation of the line passing through the above two points is
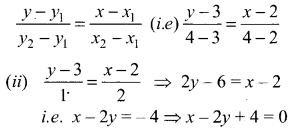
(iii) When x = 0, 2y = 4 ⇒ y = 2 cm
(iv) When y = 9 cm, x – 18 = – 4
x = -4 + 18 = 14 kg
(v) When x = 6 (kg), 6 – 2y = – 4, -2y = -4 – 6 = -10
⇒ 2y = 10 ⇒ y = 10/2 = 5 cm.
Question 14.
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5 kg includes the empty cylinders tare weight of 15.3 kg.). If it is use with constant rate then it lasts for 24 days. Then the new cylinder is replaced
(i) Find the equation relating the quantity of gas in the cylinder to the days.
(ii) Draw the graph for first 96 days.
Solution:
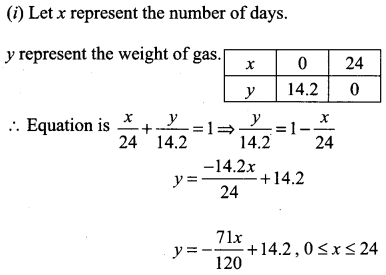
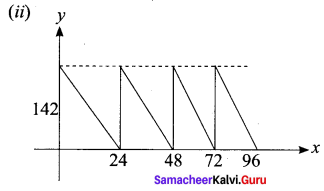
Question 15.
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find
(i) The minimum total length of the escalator,
(ii) The heights at which the escalator changes its direction,
(iii) The slopes of the escalator at the turning points.
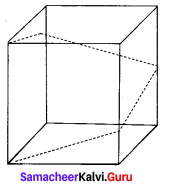
Solution:
(i) the minimum total length of the escalator.
Shape of the hall in the shopping mall is cuboid. When you open out the cuboid, the not of the cuboid will be as shown in the following diagram.
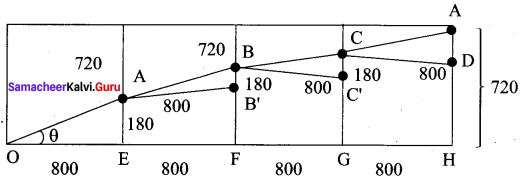
The path of the escalator is from OA to AB to BC to CD

The minimum length = 3280 units
(ii) The height at which the escalator changes its direction.

(iii) Slope of the escalator at the turning points

Since ∆OAE = ∆ABB’ = ∆BCC’ = ∆CAD
Slope at the points B, C will be \(\frac{9}{40}\)
Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.2 Additional Questions Solved
Question 1.
Find the equation of a straight line on which length of perpendicular from the origin is four units and the line makes an angle of 120° with the positive direction of x – axis.
Solution:

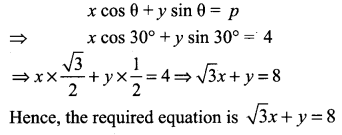
![]()
Question 2.
Find the equation of the line which passes through the point (- 4, 3) and the portion of the line intercepted between the axes is divided internally in the ratio 5 : 3 by this point.
Solution:
Let AB be a line passing through a point (-4, 3) and meets x-axis at A (a, 0) and y-axis at B (0, b).

Question 3.
If the intercept of a line between the coordinate axes is divided by the point (-5, 4) in the ratio 1 : 2, then find the equation of the line.
Solution:
Let a and b be the intercepts on the given line.
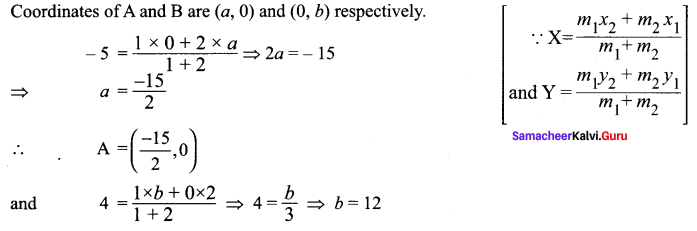
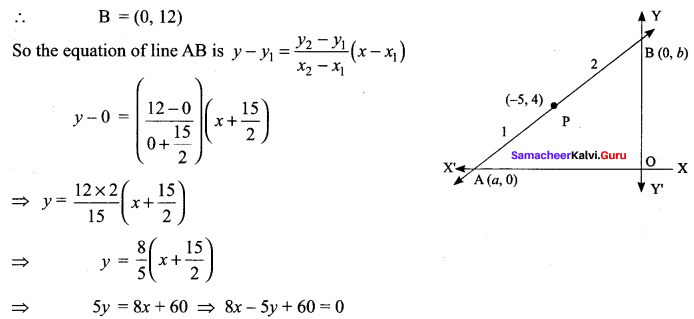
Hence, the required equation is 8x – 5y + 60 = 0
Question 4.
Find the equation of the straight line which passes through the point (1, -2) and cuts off equal intercepts from axes.
Solution:
Intercept form of a straight line is \(\frac{x}{a}+\frac{y}{b}\) = 1, where a and b are the intercepts on the axis
![]()
If equation (1) passes through the point (1, -2) we get
![]()
So, equation of the straight line is x v
![]()
Hence, the required equation x + y + 1 = 0
Question 5.
Find the distance of the line 4x – y = 0 from the point P(4, 1) measured along the line making an angle 135° with the positive x-axis
Solution:
The equation in distance form of the line passing through P(4, 1) and making an angle of 135° with the positive x-axis
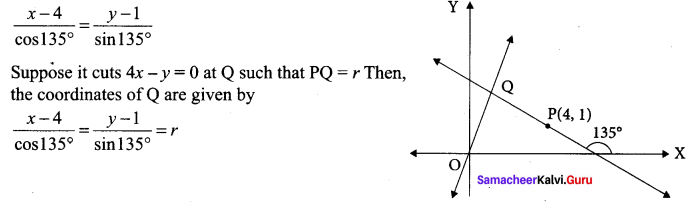

![]()
Question 6.
The line 2x – y = 5 turns about the point on it, whose ordinate and abscissa are equal, through an angle of 45° in the anti-clockwise direction, find the equation of the line in the new position.
Solution:
If the line 2x – y = 5 makes an angle θ with x – axis. Then, tan θ = 2. Let P (α, α) be a point on the line 2x – y = 5.
Then, 2 α – α = 5 ⇒ α = 5
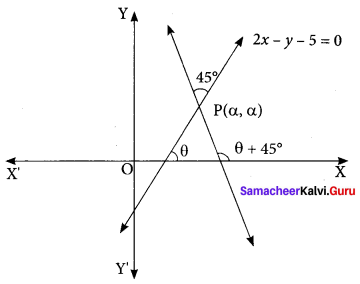
So, the coordinates of P are (5, 5). If the line 2x – y – 5 = 0 is rotated about point
P through 45° in anti clockwise direction, then the line in its new position makes angle θ + 45° with x – axis. Let m’ be the slope of the line in its new position. Then,
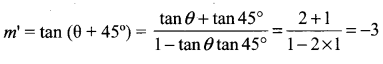
Thus, the line in its new pdsition passes through P (5, 5) and has slope m’ = -3
So, its equation y – 5 = m’ (x – 5) or, y – 5 = -3 (x – 5) or, 3x + y – 20 = 0
