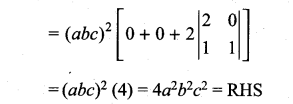Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.2

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.2

11th Maths Exercise 7.2 Question 1.
Without expanding the determinant, prove that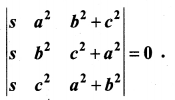
Solution:

Matrices And Determinants Class 11 Solutions Pdf Question 2.
Show that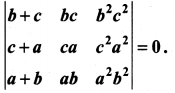
Solution:

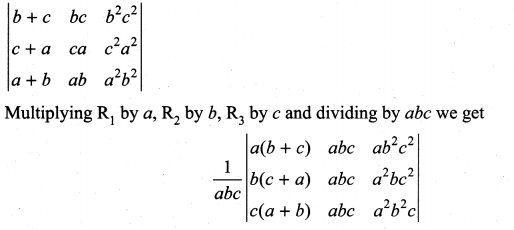
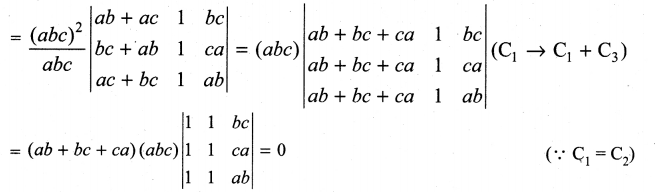
11th Maths Exercise 7.2 Answers Question 3.
Prove that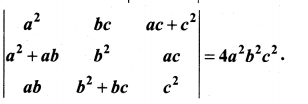
Solution:
LHS
Taking a from C₁, b from C₂ and c from C₃ we get

Expanding along R₁ we get
(2c) (abc) (1) [ab + ab] = abc (2c) (2ab)
1 = (abc) (4abc) = 4a²b²c²
= RHS

11th Maths Matrices And Determinants Solutions Question 4.

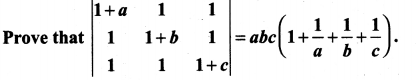
Solution:

Matrices And Determinants Class 11 State Board Solutions Question 5.
Prove that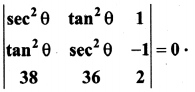
Solution:

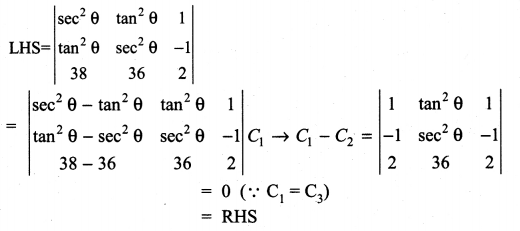
11th Maths Matrix Solutions Question 6.
Show that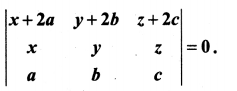
Solution:

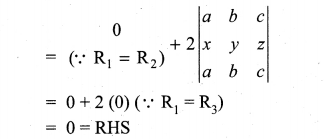
11th Maths Determinants Solutions Question 7.
Write the general form of a 3 × 3 skew-symmetric matrix and prove that its determinant is 0.
Solution:

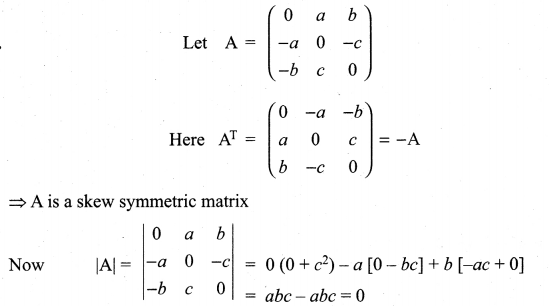
11th Maths Matrix And Determinants Question 8.

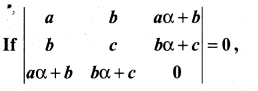
Solution:

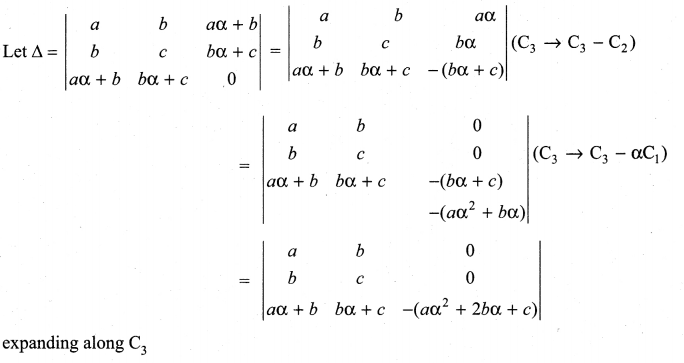
we get – (aα² + 2bα + c) [ac – b²]
So Δ = 0 ⇒ (aα² + 2bα + c) (ac -b²) = – 0 = 0
⇒ aα² + 2bα + c = 0 or ac – b² = 0
(i.e.) a is a root of ax² + 2bx + c = 0
or ac = b²
⇒ a, b, c are in G.P.

11th Maths Exercise 7.2 In Tamil Question 9.
Prove that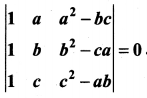
Solution:

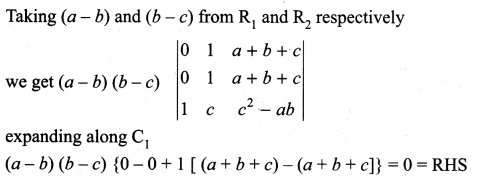
11th Std Maths Determinants Solutions Question 10.
If a, b, c are p^th, q^th and r^th terms of an A.P., find the value of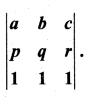
Solution:
We are given a = t_p,b = t_q and c = t_r
Let a be the first term and d be the common difference

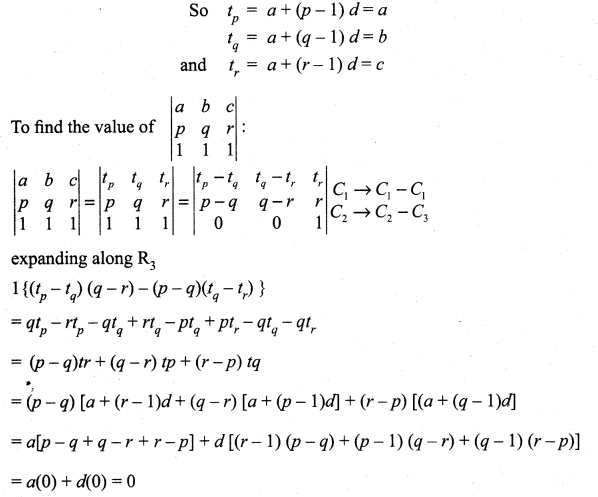
11th Maths Matrices And Determinants Pdf Question 11.
Show that 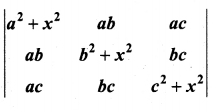is divisible by x⁴
Solution:

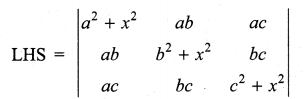
Multiplying R₁ by a, R₂ by b and R₃ by c and
taking out a from C₁ b from C₂ and c from C₃ we get
==

Class 11 Maths Exercise 7.2 Solutions Question 12.
If a, b, c are all positive, and are p^th, q^th and r^th terms of a G.P., show that

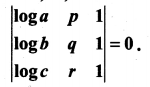
Solution:

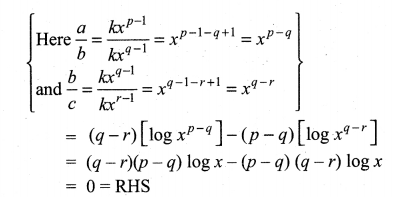
Matrices And Determinants Class 11 Solutions Question 13.
Find the value of 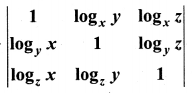if x, y, z ≠ 1.
Solution:
Expanding the determinant along R₁

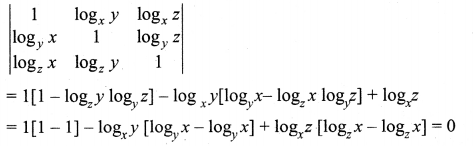
Determinants Class 11 State Board Solutions Question 14.

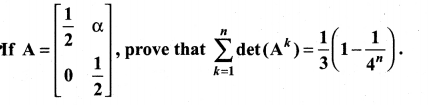
Solution:

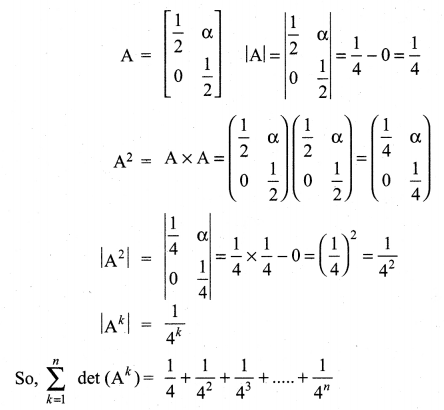
Matrices And Determinants Class 11 Exercise Question 15.
Without expanding, evaluate the following determinants:

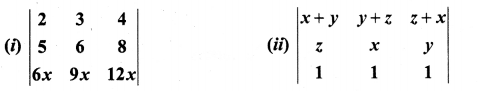
Solution:

Exercise 7.2 Class 10 Samacheer Kalvi Question 16.
If A is a square matrix and |A| = 2, find the value of |AA^T|.
Solution:
|A| = 2 (Given) |A^T| = 2
Now |AA^T| = |A| |A^T| = 2 × 2 = 4.

Chapter 7 Maths Class 11 Question 17.
If A and B are square matrices of order 3 such that |A| = -1 and |B| = 3, find the value of |3AB|.
Solution:
Given |A| = -1 : |B| = 3
Given A and B are square matrices of order 3.
∴ |kAB| = k³ |AB|
Here k = 3 ∴ |3AB| = 3³ |AB|
= 27 |AB|
= 27 (-1) (3)
= -81

Question 18.
If λ = -2, determine the value of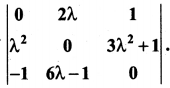
Solution:
Given λ = -2
∴ 2λ = -4; λ² = (-2)²; 3λ² + 1 = 3 (4) + 1 = 13
6λ – 1 = 6(-2) – 1 = -13

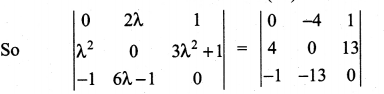
expanding along R₁
0(0) + 4 (0 + 13) + 1 (-52 + 0) = 52 – 52 = 0
Aliter: The determinant value of a skew-symmetric matrix is zero

Question 19.
Determine the roots of the equation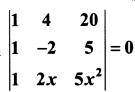
Solution:

Given the determinant value is 0
⇒ 30(1 + x) (2 – x) = 0
⇒ 1 + x = 0 or 2 – x = 0
⇒ x = -1 or x = 2
So, x = -1 or 2.

Question 20.
Verify that det (AB) = (det A) (det B) for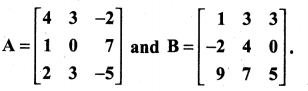
Solution:


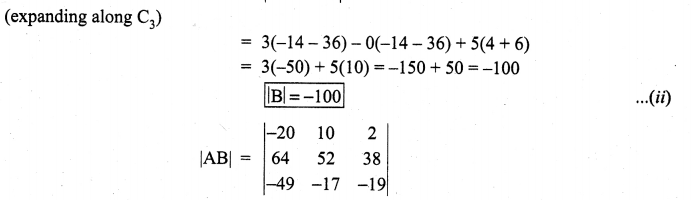
{(-20)(52) (-19) + (10)(38)(—49) + (2)(64)(-17)} – {(-49)(52) (2) + (-17)(38)(-20) + (-19)(64)(10)}
= (19760 – 18620 – 2176) – (-5096 + 12920 – 12160)
= (19760 + 5096 + 12160) – (18620 + 2176 + 12920)
= 37016 – 33716 = 3300 ….(3)
Now (1) × (2) = (3)
(i.e.,) (-33) (-100) = 3300
⇒ det (AB) = (det A), (det B)

Question 21.
Using cofactors of elements of second row, evaluate |A|, where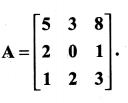
Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.2 Additional Problems

Question 1.

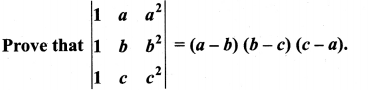
Solution:

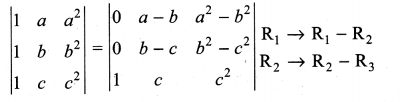
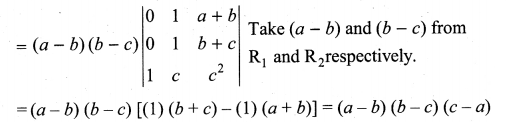
Question 2.

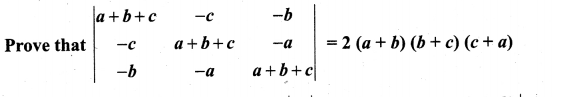
Solution:

Question 3.

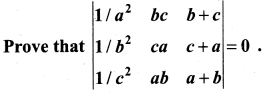
Solution:

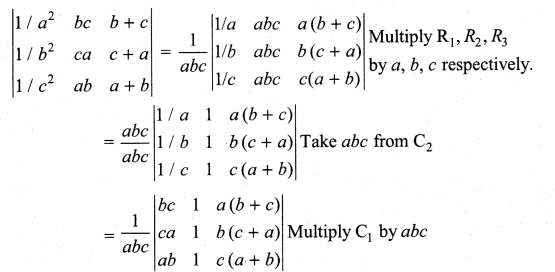
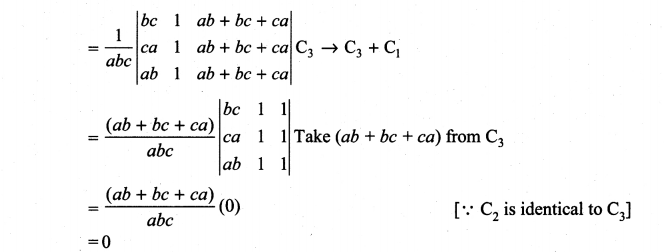
Question 4.

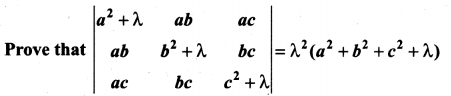
Solution:

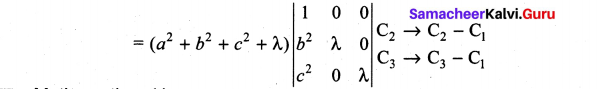
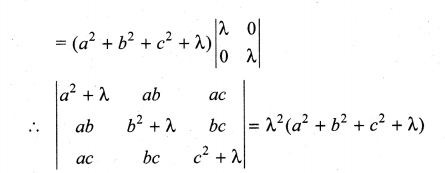
Question 5.

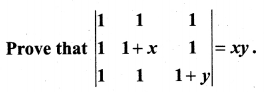
Solution:

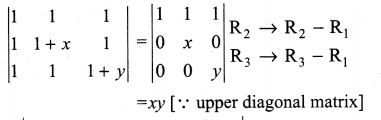
Question 6.

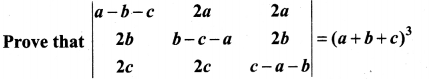
Solution:

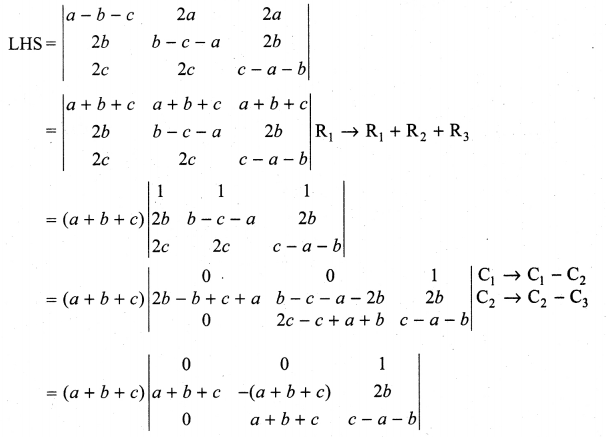
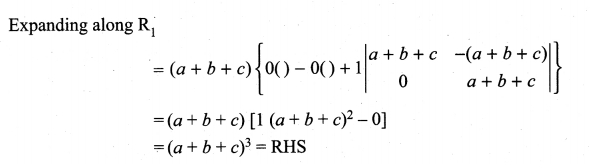
Question 7.

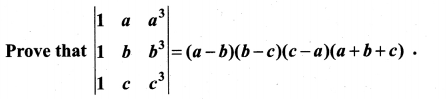
Solution:

Question 8.

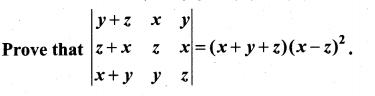
Solution:

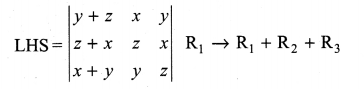
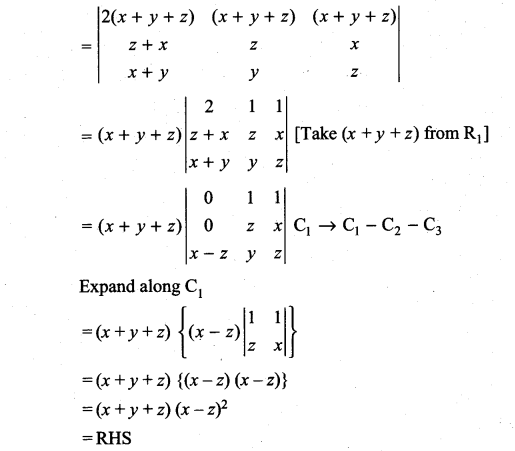
Question 9.

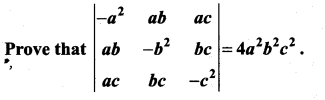
Solution: