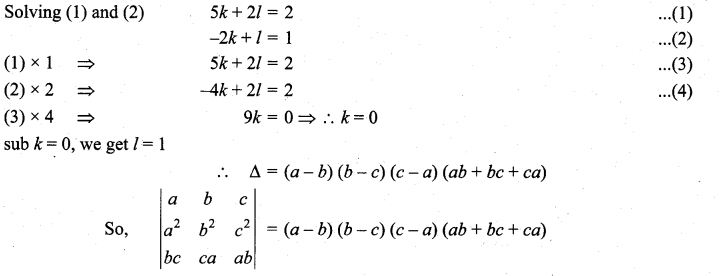You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.3
Solve the following problems by using factor theorem
Question 1.
Show that <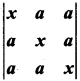 = (x – a)2 (x + 2a)
= (x – a)2 (x + 2a)
Solution:

⇒ (x + 2d) is a factor of A.
Now degree of Δ is 3 (x × x × x = x3) and we have 3 factors for A
∴ There can be a constant as a factor for A.
(i.e.,) Δ = k(x – a)2 (x + 2d)
equating coefficient of x3 on either sides we get k = 1
![]()
∴ Δ = (x – a)2 (x + 2a)
Question 2.
Show that 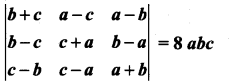
Solution:
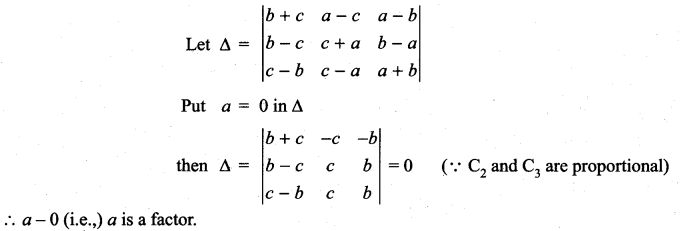
Similarly b and c are factors of Δ.
The product of the leading diagonal elements is (b + c) (c + a) (a + b)
The degree is 3. And we got 3 factors for Δ ∴ m = 3 – 3 = 0
∴ there can be a constant k as a factor for Δ.
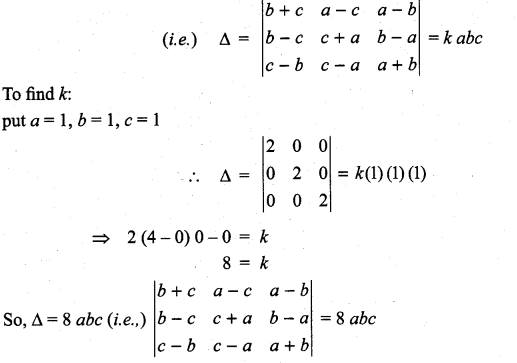 >
>
Question 3.
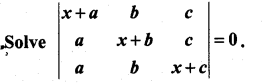
Solution:
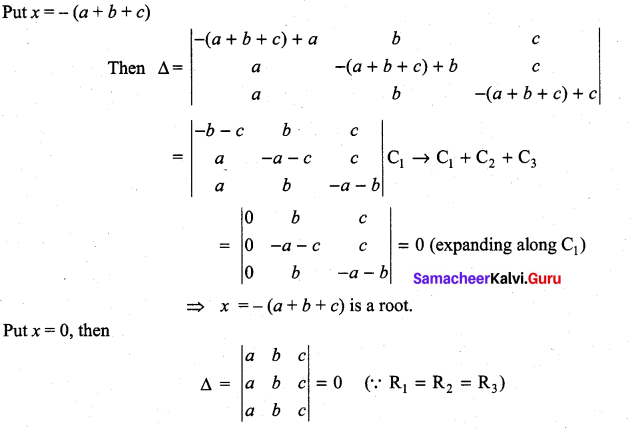
⇒ x = 0, 0 are roots.
Now the degree of the leading diagonal elements is 3.
∴ the equation is of degree 3, so the roots are 0, 0, – (a + b + c)
![]()
Question 4.
Show that 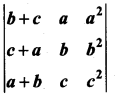 = (a + b + c) (a – b) (b – c) (c – a)
= (a + b + c) (a – b) (b – c) (c – a)
Solution:
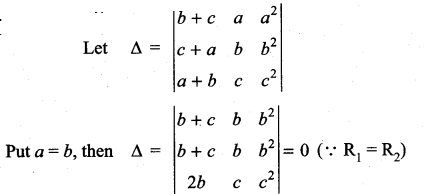
⇒ (a – b) is a factor of Δ.
Similarly (b – c) and (c – a) are factors of Δ.
The degree of the product of elements along leading diagonal is 1 + 1 + 2 = 4 and we got 3 factors for Δ. m = 4 – 3 = 1
∴ There can be one more factor symmetric with a, b, c which is of the form k (a + b + c).
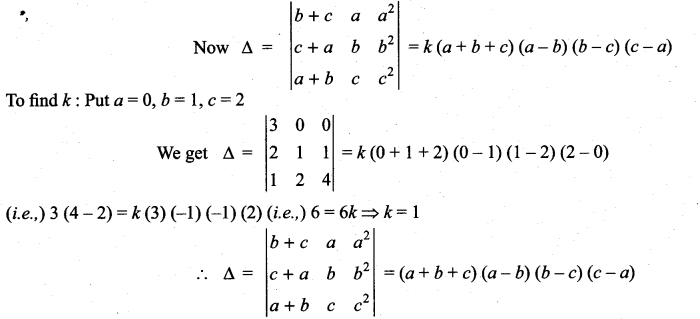
Question 5.
Solve 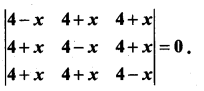
Solution:
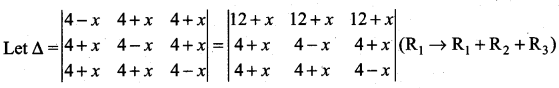

Question 6.
Show that 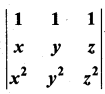 = (x – y) (y – z) (z – x)
= (x – y) (y – z) (z – x)
Solution:
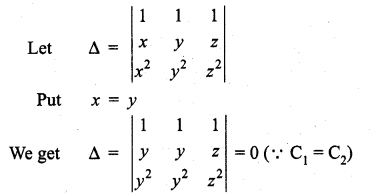
⇒ (x – y) is a factor of Δ.
Similarly (y – z) and (z – x) are factors of Δ.
Now degree of Δ = 0 + 1 + 2 = 3 and we have 3 factors of Δ.
and so there can be a constant k as a factor of Δ.
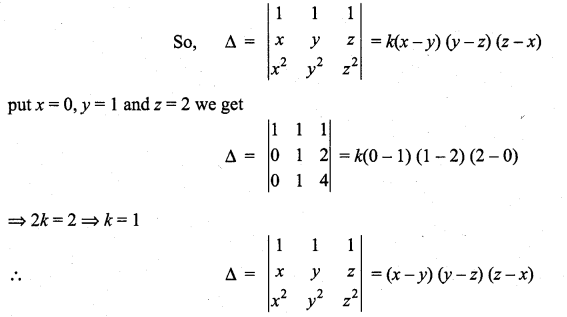
![]()
Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.3 Additional Problems
Question 1.
Prove that 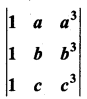 = (a – b) (b – c) (c – a) (a + b + c).
= (a – b) (b – c) (c – a) (a + b + c).
Solution:
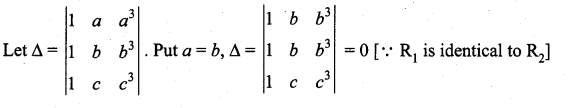
∴ (a – b) is a factor of Δ.
Similarly we observe that Δ is symmetric in a, b, c by putting b = c, c = a, we get Δ = 0. Hence (b – c) and (c – a) are also factors of Δ.
∴ The product (a – b) (b – c) (c – a) is a factor of Δ. The degree of this product is 3. The product of leading diagonal elements is 1. bc3. The degree of this product is 4.
∴ By cyclic and symmetric properties, the remaining symmetric factor of first degree must be k (a + b + c), where k is any non-zero constant.

Question 2.
Using factor method show that 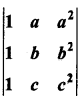 = (a – b) (b – c) (c – a)
= (a – b) (b – c) (c – a)
Solution:
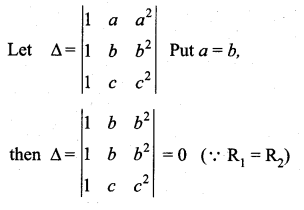
⇒ (a – b) is a factor of Δ.
similarly (b – c) and (c – a) are factors of Δ.
The product of leading diagonal elements is bc2. The degree of the product is 1 + 2 = 3.
∴ there will be three factors for Δ. We got 3 factors for Δ as (a – b), (b – c) and (c – a). Its degree = 3. ∴ m = 3 – 3 = 0
∴ there can be a constant k as a factor of Δ.

![]()
Question 3.
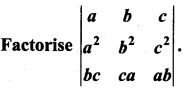
Solution:
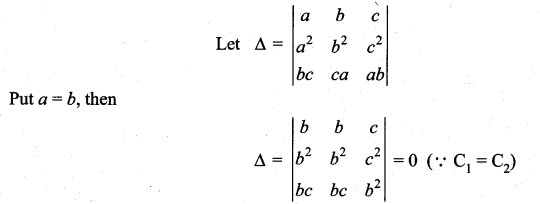
⇒ (a – b) is a factor of A.
Similarly (b – c) and (c – a) are factors of Δ.
The degree of Δ = 5 and degree of product of factors = 3.