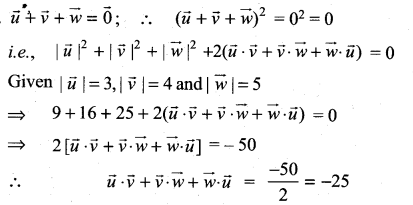Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.3

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.3

Question 1.
Find \(\vec{a} \cdot \vec{b}\) when

Solution:

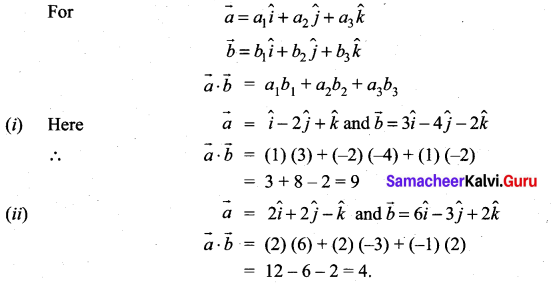
Question 2.
Find the value of λ for which the vectors \(\vec{a}\) and \(\vec{b}\) are perpendicular, where

Solution:
When \(\vec{a}\) and \(\vec{b}\) are ⊥^r then \(\vec{a} \cdot \vec{b}\) = 0
\(\vec{a}\) ⊥^r \(\vec{b}\) ⇒ \(\vec{a} \cdot \vec{b}\) = 0
(i) (2) (1) + (λ) (-2) + (1) (3) = 0 ⇒ λ = 5/2
(ii) (2) (3) + (4) (-2) + (-1) (λ) = 0
6 – 8 – λ = 0
-λ – 2 = 0 ⇒ -λ = 2 ⇒ λ = -2

Question 3.
If \(\vec{a}\) and \(\vec{b}\) are two vectors such that |\(\vec{a}\)| = 10, |\(\vec{b}\)| = 15 and \(\vec{a} \cdot \vec{b}\) = 75\(\sqrt{2}\) , find the angle between \(\vec{a}\) and \(\vec{a}\) .
Solution:

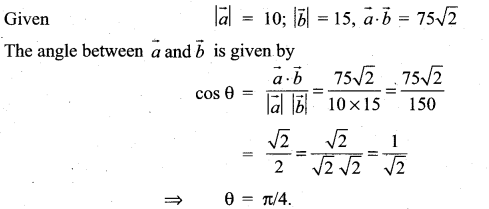
Question 4.
Find the angle between the vectors

Solution:

Question 5.
If \(\overrightarrow{\boldsymbol{a}}, \overrightarrow{\boldsymbol{b}}, \overrightarrow{\boldsymbol{c}}\) are three vectors such that \(\vec{a}+2 \vec{b}+\vec{c}=\overrightarrow{0}\) and \(|\vec{a}|=3,|\vec{b}|=4,|\vec{c}|=7\) find the angle between \(\vec{a}\) and \(\vec{b}\)
Solution:

Question 6.
Show that the vectors are mutually orthogonal.
Solution:

Question 7.
Show that the vectors form a right angled triangle.
Solution:

So, the given vectors form the sides of a right angled triangle

Question 8.

Solution:

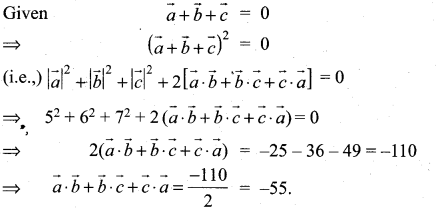
Question 9.
Show that the points (2, -1, 3) (4, 3, 1) and (3, 1, 2) are collinear
Solution:
Let the given points be A, B, C

Question 10.
If \(\vec{a}, \vec{b}\) are unit vectors and θ is the angle between them, show that

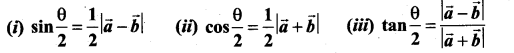
Solution:

Question 11.
Let \(\vec{a}, \vec{b}, \vec{c}\) be the three vectors such that \(|\vec{a}|=3,|\vec{b}|=4,|\vec{c}|=5\) and each one of them being perpendicular to the sum of the other two, find \(|\vec{a}+\vec{b}+\vec{c}|\)
Solution:

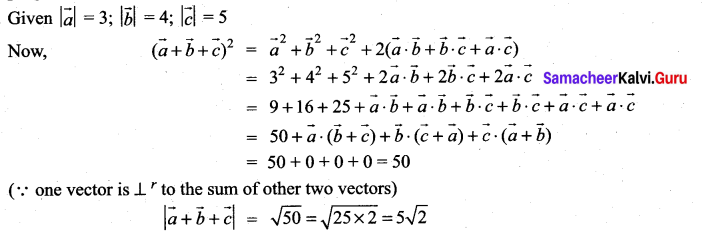
Question 12.
Find the projection of the vector \(\hat{i}+3 \hat{j}+7 \hat{k}\) on the vector \(2 \hat{i}+6 \hat{j}+3 \hat{k}\)
Solution:

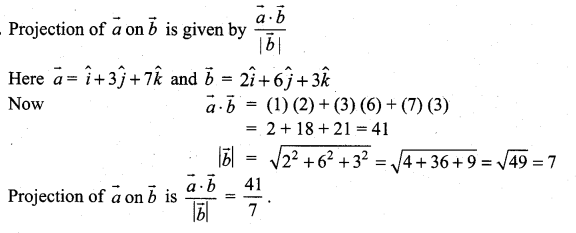
Question 13.
Find λ, when the projection of is 5 units.
Solution:

Question 14.

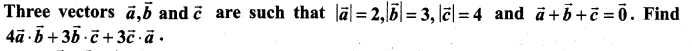
Solution:

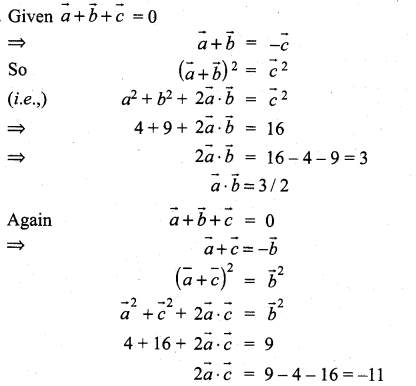
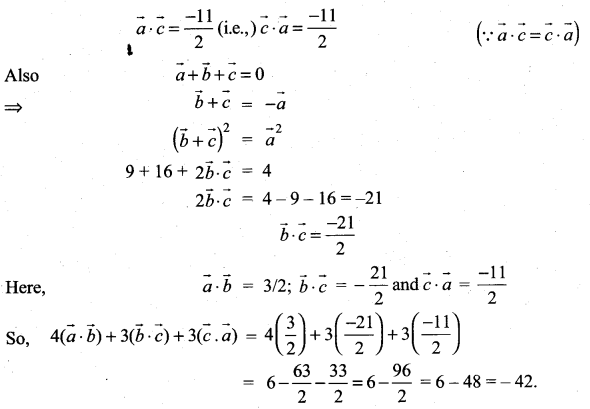
Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.3 Additional Problems

Question 1.
Find λ so that the vectors are perpendicular to each other.
Solution:

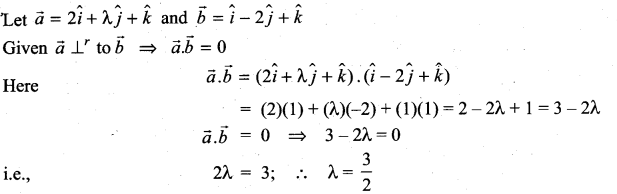
Question 2.

Solution:

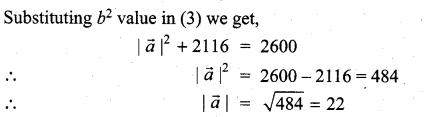
Question 3.
If the sum of two unit vectors is a unit vector prove that the magnitude of their difference is \(\sqrt{3}\)
Solution:

Question 4.
Show that the vectors form a right angled triangle.
Solution:

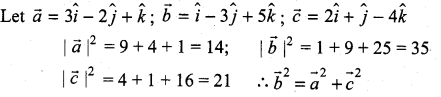
⇒ The given vectors form the sides of a right of a right angled triangle.

Question 5.
Find the projection of

Solution:

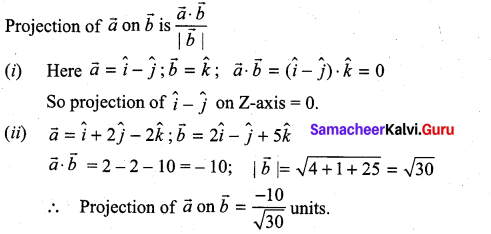
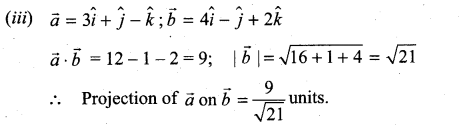
Question 6.
Show that the vector \(\hat{i}+\hat{j}+\hat{k}\) is equally inclined with the coordinate axes.
Solution:

Question 7.
If \(\vec{a}, \vec{b}, \vec{c}\) are three mutually perpendicular unit vectors, then prove that \(|\vec{a}+\vec{b}+\vec{c}|=\sqrt{3}\)
Solution:

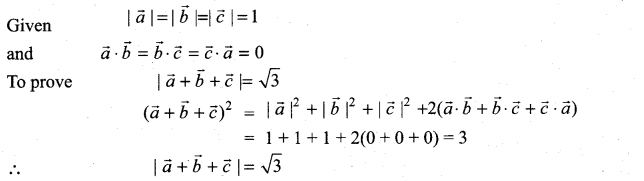
Question 8.
Show that the points whose positions vectors from a right angled triangle.
Solution:

⇒ The given points form a right angled triangle.

Question 9.

Solution: