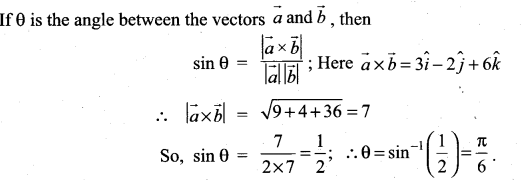You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.4
Question 1.
Find the magnitude of ![]()
Solution:

Question 2.
Show that ![]()
Solution:

Question 3.
Find the vectors of magnitude \(10 \sqrt{3}\) that are perpendicular to the plane which contains \(\hat{i}+2 \hat{j}+\hat{k}\) and \(\hat{i}+3 \hat{j}+4 \hat{k}\)
Solution:
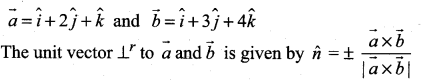
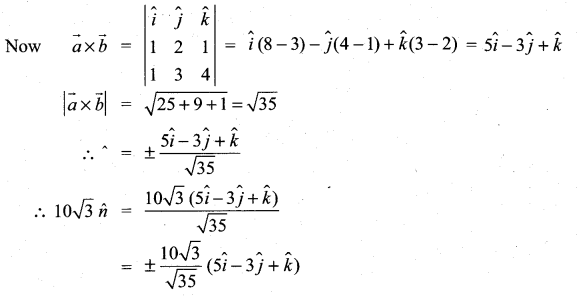
![]()
Question 4.
Find the unit vectors perpendicular to each of the vectors
![]()
Solution:
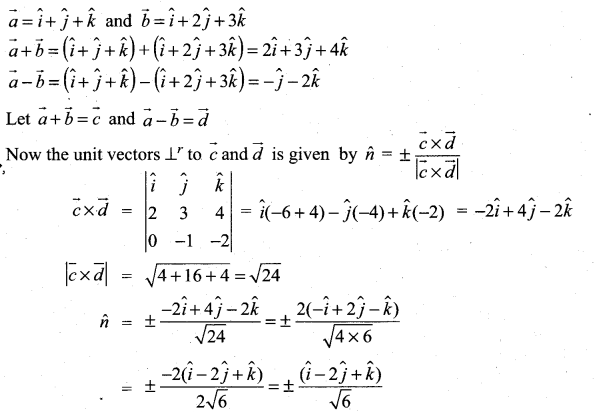
Question 5.
Find the area of the parallelogram whose two adjacent sides are determined by the vectors \(\hat{i}+2 \hat{j}+3 \hat{k}\) and \(3 \hat{i}-2 \hat{j}+\hat{k}\)
Solution:

Question 6.
Find the area of the triangle whose vertices are A(3, -1, 2), B(1, -1, -3) and C(4, -3, 1)
Solution:
A = (3, -1, 2); B = (1, -1, -3) and C = (4, -3, 1)

Question 7.
If \(\vec{a}, \vec{b}, \vec{c}\) are position vectors of the vertices A, B, C of a triangle ABC, show that the area of the triangle ABC is \(\frac{1}{2}|\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}|\). Also deduce the condition for collinearity of the points A, B, C
Solution:

If the points A, B, C are collinear, then the area of ∆ABC = 0.
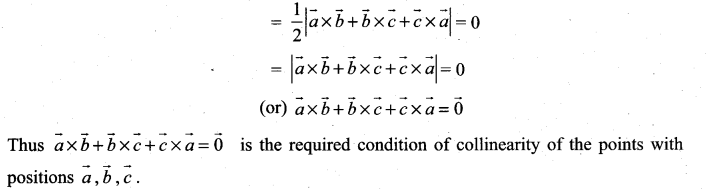
Question 8.
For any vector \(\vec{a}\) prove that ![]()
Solution:
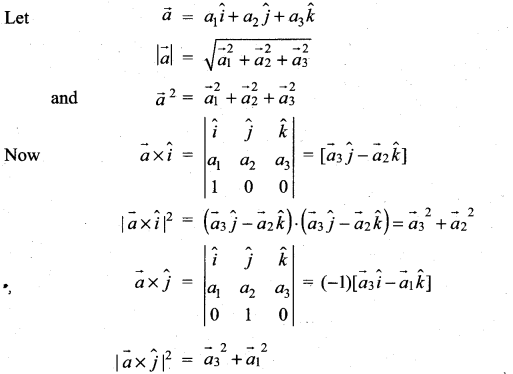
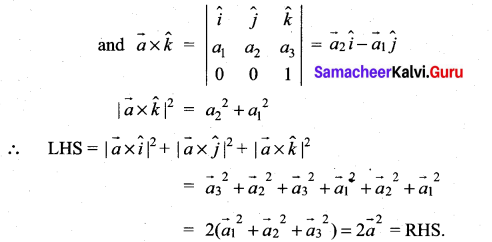
![]()
Question 9.
Let \(\vec{a}, \vec{b}, \vec{c}\) be unit vectors such that \(\overrightarrow{\boldsymbol{a}} \cdot \overrightarrow{\boldsymbol{b}}=\overrightarrow{\boldsymbol{a}} \cdot \overrightarrow{\boldsymbol{c}}=\mathbf{0}\) and the angle between \(\vec{b} \text { and } \vec{c} \text { is } \frac{\pi}{3}\). Prove that \(\vec{a}=\pm \frac{2}{\sqrt{3}}(\vec{b} \times \vec{c})\)
Solution:
Given \(|\vec{a}|=|\vec{b}|=|\vec{c}|\) = 1
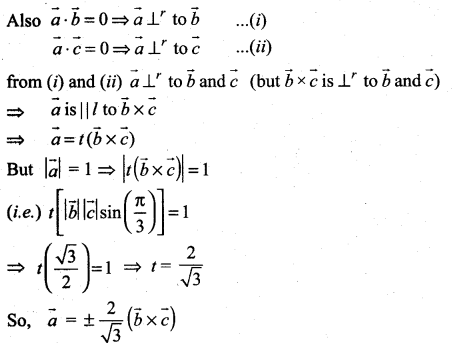
Question 10.
Find the angle between the vectors ![]() using vector product
using vector product
Solution:
The angle between \(\vec{a}\) and \(\vec{b}\) using vector product is given by
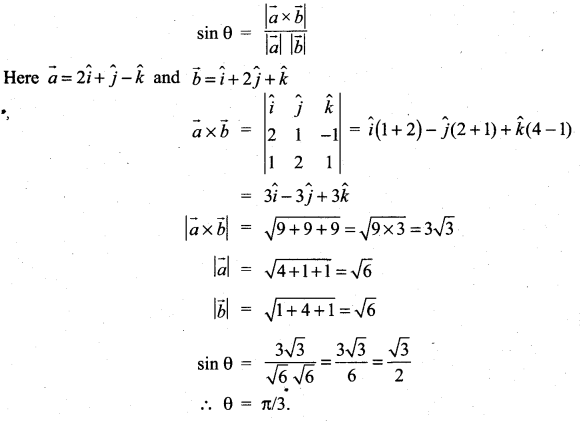
Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.4 Additional Problems
Question 1.
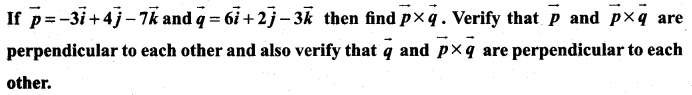
Solution:

Question 2.
If \(\vec{a}\), \(\vec{b}\) are any two vectors, then prove that ![]()
Solution:
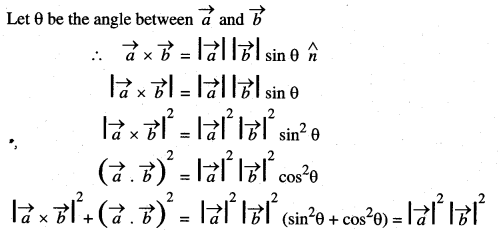
Question 3.
Find the angle between the vectors ![]() by using cross product.
by using cross product.
Solution:
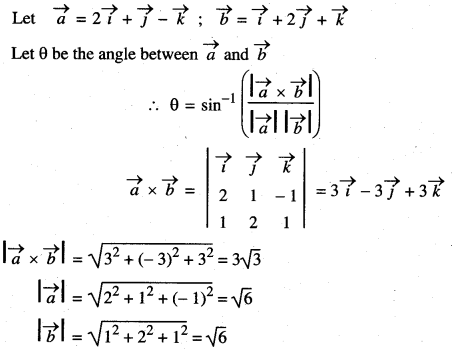
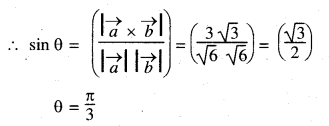
Question 4.
Find the vector of magnitude 6 which are perpendicular to both the vectors ![]()
Solution:

Question 5.
Find the vectors whose length 5 which are perpendicular to the vectors ![]()
Solution:
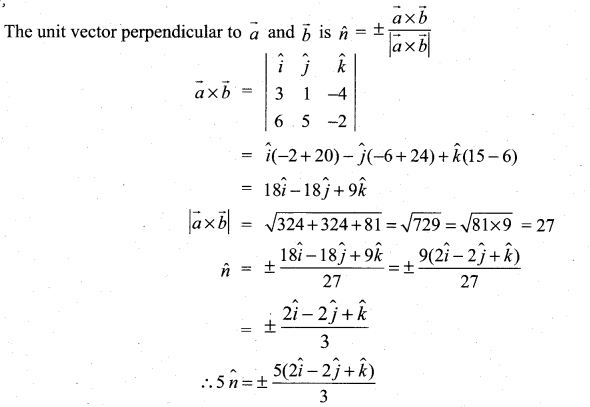
![]()
Question 6.
![]()
Solution:
Given \(\vec{a} \times \vec{b}=\vec{c} \times \vec{d}\) and \(\vec{a} \times \vec{c}=\vec{b} \times \vec{d}\)
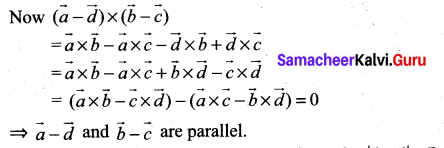
Question 7.
Find the angle between two vectors \(\vec{a}\) and \(\vec{b}\) if \(|\overrightarrow{\boldsymbol{a}} \times \overrightarrow{\boldsymbol{b}}|=\overrightarrow{\boldsymbol{a}} \cdot \overrightarrow{\boldsymbol{b}}\)
Solution:
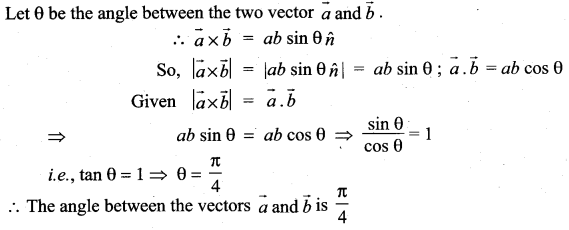
Question 8.
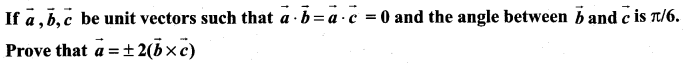
Solution:

Question 9.
If ![]() find the angle between \(\vec{a}\) and \(\vec{b}\)
find the angle between \(\vec{a}\) and \(\vec{b}\)
Solution: