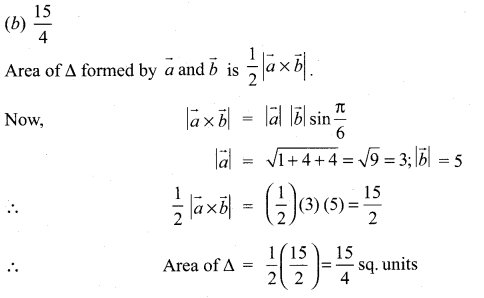Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.5

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.5

Choose the correct or the most suitable answer from the given four alternatives:

Question 1.
The value of \(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{CD}}\) is ………………

Solution:
(c) \(\overrightarrow{0}\)

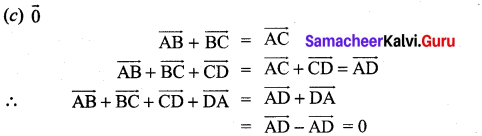
Question 2.
If \(\vec{a}+2 \vec{b}\) and \(3 \vec{a}+m \vec{b}\) are parallel, then the value of m is ………………
(a) 3
(b) \(\frac{1}{3}\)
(c) 6
(d) \(\frac{1}{6}\)
Solution:
(c) 6

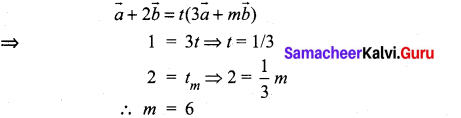
Question 3.
The unit vector parallel to the resultant of the vectors \(\hat{i}+\hat{j}-\hat{k}\) and \(\hat{i}-2 \hat{j}+\hat{k}\) is ………………

Solution:

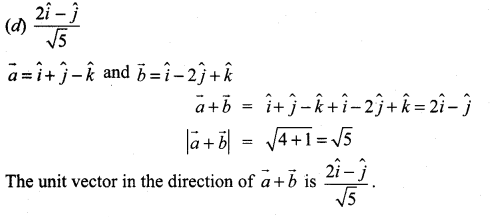
Question 4.
A vector \(\overrightarrow{O P}\) makes 60° and 45° with the positive direction of the x and y axes respectively. Then the angle between \(\overrightarrow{O P}\) and the z-axis is …………….
(a) 45°
(b) 60°
(c) 90°
(d) 30°
Solution:
(b) 60°
α = 60°, β = 45°
We know cos²α + cos²β + cos²γ = 1
(i.e.,) \(\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{\sqrt{2}}\right)^{2}\) + cos²γ = 1
cos²γ = 1 – \(\frac{1}{4}-\frac{1}{2}=\frac{1}{4}\)
cos γ = \(\frac{1}{2}\) ⇒ y = π/3 = 60°

Question 5.
If \(\overrightarrow{B A}=3 \hat{i}+2 \hat{j}+\hat{k}\) and the position vector of B is \(\hat{i}+3 \hat{j}-\hat{k}\), then the position vector A is …………………

Solution:

Question 6.
A vector makes equal angle with the positive direction of the coordinate axes. Then each angle is equal to …………..

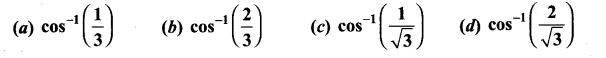
Solution:

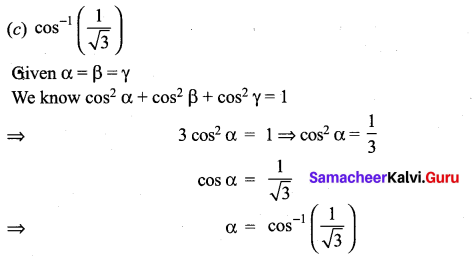
Question 7.
The vectors \(\vec{a}-\vec{b}, \vec{b}-\vec{c}, \vec{c}-\vec{a}\) are ……………
(a) parallel to each other
(b) unit vectors
(c) mutually perpendicular vectors
(d) coplanar vectors
Solution:
(d) coplanar vectors

Question 8.
If ABCD is a parallelogram, then \(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{C B}+\overrightarrow{C D}\) is equal to ……………

Solution:

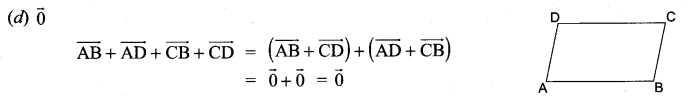
Question 9.
One of the diagonals of parallelogram ABCD with \(\vec{a}\) and \(\vec{b}\) as adjacent sides is \(\vec{a}+\vec{b}\). The other diagonal \(\overrightarrow{\mathrm{BD}}\) is ……………

Solution:

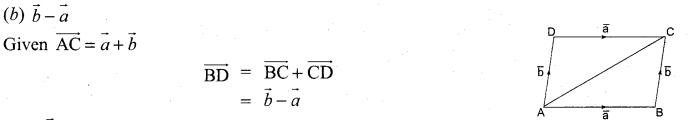
Question 10.
If \(\vec{a}\), \(\vec{b}\) are the position vectors A and B, then which one of the following points whose position vector lies on AB, is ………….

Solution:
(c) \(\frac{2 \vec{a}+\vec{b}}{3}\)

Question 11.
If \(\vec{a}, \vec{b}, \vec{c}\) are the position vectors of three collinear points, then which of the following is true?

Solution:
(b) \(2 \vec{a}=\vec{b}+\vec{c}\)

Question 12.
If \(\vec{r}=\frac{9 \vec{a}+7 \vec{b}}{16}\), then the point P whose position vector \(\vec{r}\) divides the line joining the points with position vectors \(\vec{a}\) and \(\vec{b}\) in the ratio ………………
(a) 7 : 9 internally
(b) 9 : 7 internally
(c) 9 : 7 externally
(d) 7 : 9 externally
Solution:

Question 13.
If \(\lambda \hat{i}+2 \lambda \hat{j}+2 \lambda \hat{k}\) is a unit vector, then the value of λ is ……………..
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{9}\)
(d) \(\frac{1}{2}\)
Solution:

Question 14.
Two vertices of a triangle have position vectors \(3 \hat{i}+4 \hat{j}-4 \hat{k}\) and \(2 \hat{i}+3 \hat{j}+4 \hat{k}\) .If the position vector of the centroid is \(\hat{i}+2 \hat{j}+3 \hat{k}\), then the position vector of the third vertex is ………………….

Solution:

Question 15.

(a) 42
(b) 12
(c) 22
(d) 32
Solution:
(c) 22

Question 16.
If \(\vec{a}\) and \(\vec{b}\) having same magnitude and angle between them is 60° and their scalar product is \(\frac{1}{2}\) then \(|\vec{a}|\) is ……………
(a) 2
(b) 3
(c) 7
(d) 1
Solution:
(d) 1

Question 17.
The value of θ ∈ (0, \(\frac{\pi}{2}\)) for which the vectors are perpendicular, is equal to …………………

Solution:

Question 18.

(a) 15
(b) 35
(c) 45
(d) 25
Solution:
(d) 25

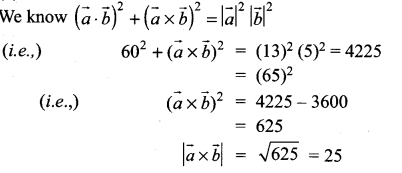
Question 19.
Vectors \(\vec{a}\) and \(\vec{b}\) are inclined at an angle θ = 120°
is equal to ………….
(a) 225
(b) 275
(c) 325
(d) 300
Solution:
(d) 300

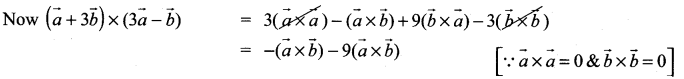
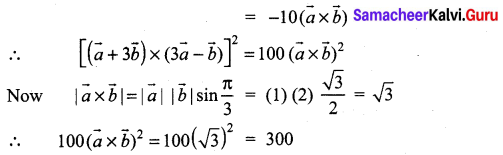
Question 20.
If \(\vec{a}\) and \(\vec{b}\) are two vectors of magnitude 2 and inclined at an angle 60°, then the angle between \(\vec{a}\) and \(\vec{a}+\vec{b}\) is ………………
(a) 30°
(b)60°
(c) 45 °
(d) 90°
Solution:
(a) 30°

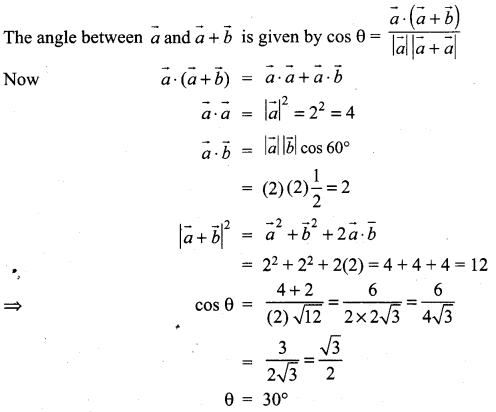
Question 21.
If the projection of \(5\hat{i} -\hat{j}-3 \hat{k}\) on the vector \(\hat{i}+3 \hat{j}+\lambda \hat{k}\) is same as the projection of \(\hat{i}+3 \hat{j}+\lambda \hat{k}\) on \(5\hat{i}- \hat{j}-3 \hat{k}\) then λ is equal to ………………
(a) ±4
(b) ±3
(c) ±5
(d) ±1
Solution:
(c) ±5

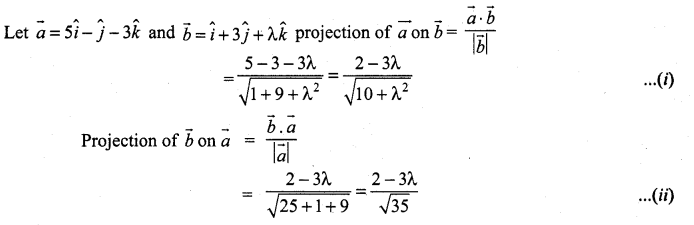
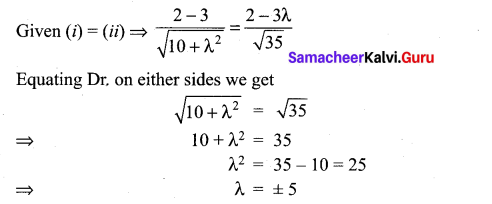
Question 22.
If (1, 2, 4) and (2, – 3λ, – 3) are the initial and terminal points of the vector \(\hat{i}+5 \hat{j}-7 \hat{k}\), then the value of λ is equal to ……………..
(a) \(\frac{7}{3}\)
(b) \(-\frac{7}{3}\)
(c) \(-\frac{5}{3}\)
(d) \(\frac{5}{3}\)
Solution:

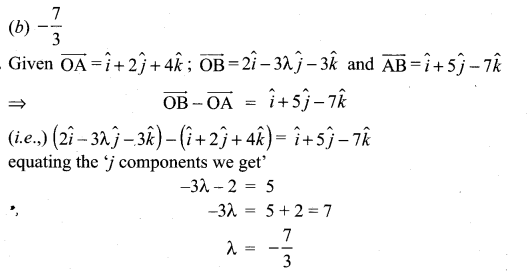
Question 23.
If the points whose position vector \(10 \hat{i}+3 \hat{j}, 12 \hat{i}-5 \hat{j}\) and \(\vec{a} \hat{i}+11 \hat{j}\) are collinear then a is equal to ………………
(a) 6
(b) 2
(c) 5
(d) 8
Solution:
(d) 8

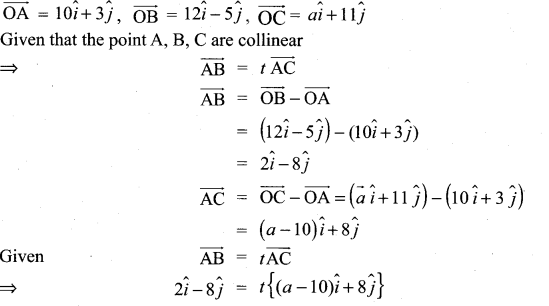
equating \(\hat{j}\) components
⇒ -8 = 8t ⇒ t = -1
equation \(\hat{i}\) components
t(a – 10) = 2
(i.e.,) (-1) (a – 10) = 2
a – 10 = -2
a = – 2 + 10 = -8

Question 24.
If then x is equal to …………..
(a) 5
(b) 7
(c) 26
(d) 10
Solution:
(c) 26

Question 25.
If \(\vec{a}=\hat{i}+2 \hat{j}+2 \hat{k},|\vec{b}|=5\) and the angle between \(\vec{a}\) and \(\vec{b}\) is \(\frac{\pi}{6}\), then the area of the triangle formed by these two vectors as two sides, is …………….
(a) \(\frac{7}{4}\)
(b) \(\frac{15}{4}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{17}{4}\)
Solution: