You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.5
Question 1.
Prove that f(x) = 2x2 + 3x – 5 is continuous at all points in R.
Solution:
Polynomial functions are continuous at every points of R.
![]()
Question 2.
Examine the continuity of the following:
(i) x + sin x
Solution:
f(x) = x + sin x
The Domain of the function (-∞, ∞)
∴ f(x) is continuous in (-∞, ∞)(i.e.,) for all x ∈ R
(ii) x2 cos x
Solution:
f(x) = x2 cos x
The Domain of the function (-∞, ∞)
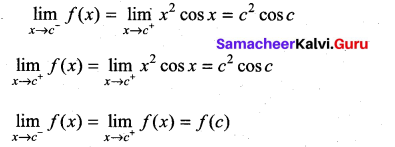
f(x) is continuous in R
(iii) ex tan x
Solution:
The Domain of the function in R – {(2n + 1) π/2}
∴ The functions is continuous for all x ∈ R – (2n + 1) \(\frac{\pi}{2}\), n ∈ Z
(iv) e2x + x2
f(x) = e2x + x2 = 1 + 2x + \(\frac{(2 x)^{2}}{2 !}\) + …………. + x2
Solution:
∴ The functions is continuous for all x ∈ R
(v) x.ln x
Solution:
Thus f(x) is continuous for (0, ∞)
(vi) \(\frac{\sin x}{x^{2}}\)
Solution:
Thus f(x) is continuous for all x ∈ R – {0}
(vii) \(\frac{x^{2}-16}{x+4}\)
Solution:
f(x) = \(\frac{x^{2}-16}{x+4}=\frac{(x-4)(x+4)}{x+4}\)
The function f(x) is continuous for all x ∈ R – {-4}
(viii) |x + 2| + |x – 1|
Solution:
f(x) is continuous for x ∈ R
(ix) \(\frac{|x-2|}{|x+1|}\)
Solution:
The function is continuous for all x ∈ R – {-1}
(x) cot x + tan x
Solution:
The function is continuous for all x ∈ R – \(\frac{n \pi}{2}\), n ∈ z.
![]()
Question 3.
Find the points of discontinuity of the function f, where,
(i)
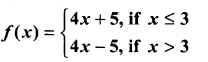
Solution:
f(3) = 12 + 5 = 17

∴ f(x) is discontinuous at x = 3
(ii)
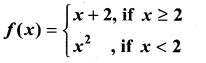
Solution:
f(x) = 4
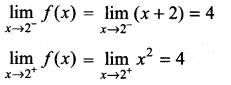
∴ f(x) is continuous for all x ∈ R
(iii)
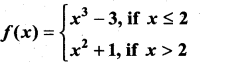
Solution:
f(x) = 8 – 3 = 5
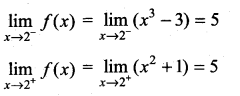
∴ f(x) is continuous for all x ∈ R
(iv)
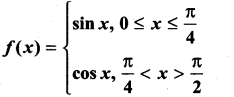
Solution:
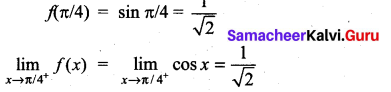
∴ f(x) is continuous for all x ∈ [0, π/2]
![]()
Question 4.
At the given points x0 discover whether the given function is continuous or discontinuous citing the reasons for your answer.
(i)
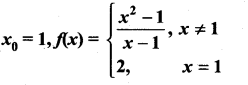
Solution:
Given f(x0) = 1
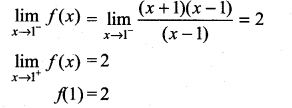
∴ f(x) is continuous at x0 = 1
(ii)
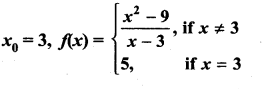
Solution:
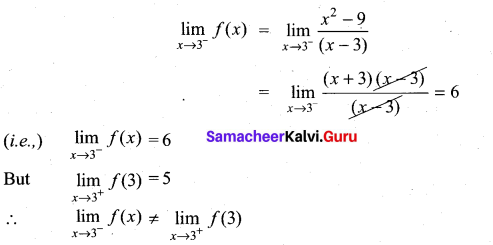
∴ f(x) is not continuous at x0 = 3
Question 5.
Show that the function 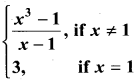 is continuous on (-∞, ∞)
is continuous on (-∞, ∞)
Solution:
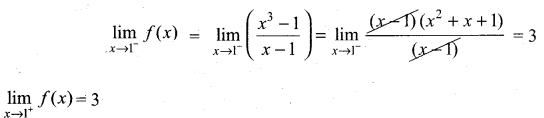
Given that f(1) = 3
∴ f(x) is continuous for all x ∈ R
Question 6.
For what value of α is this function f(x) = 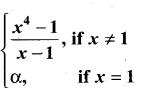 continuous at x = 1?
continuous at x = 1?
Solution:

∵ f(x) is continuous at x = 1, α = 4
Question 7.
Let 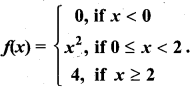 Graph the function. Show that f(x) continuous on (-∞, ∞)
Graph the function. Show that f(x) continuous on (-∞, ∞)
Solution:
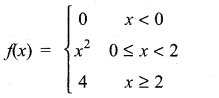
∴ f(x) is continuous in (-∞, ∞)
Question 8.
If f and g are continuous function with f(3) = 5 and ![]() find g(3).
find g(3).
Solution:
Since f and g are continuous
![]()
2f(3) – g(3) = 4
2(5) – g(3) = 4
10 – 4 = g(3)
g(3) = 6
![]()
Question 9.
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
(i)
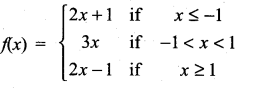
∴ f(x) is not continuous at x = 1
Solution:
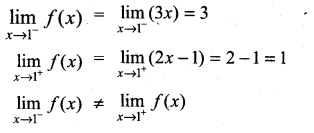
f(x) is not continuous at x = 1
(ii)
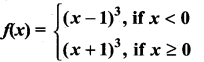
Solution:
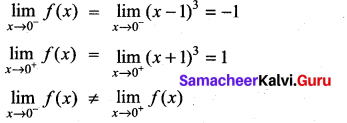
∴ f(x) is not continuous at x = 0
Question 10.
A function f is defined as follows:
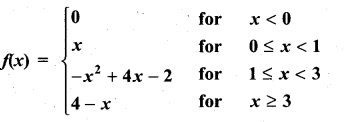
Is the function continuous?
Solution:
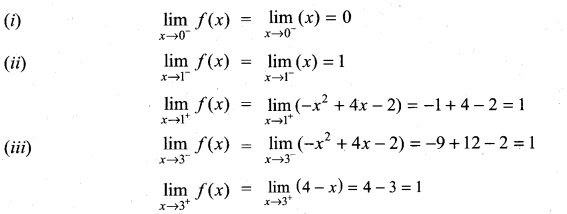
From (i), (ii) and (iii)
f(x) is continuous at x = 0, 1, 3
Question 11.
Which of the following functions f has removable discontinuity at x = x0? If the discontinuity is removable, find a function g that agrees with f for x ≠ x0 and is continuous on R.
(i) f(x) = \(\frac{x^{2}-2 x-8}{x+2}\), x0 = -2
Solution:
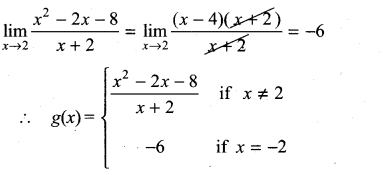
(ii) f(x) = \(\frac{x^{3}+64}{x+4}\), x0 = -4
Solution:
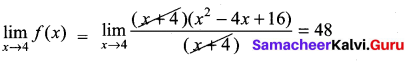
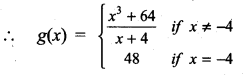
(iii) f(x) = \(\frac{3-\sqrt{x}}{9-x}\), x0 = 9
Solution:

Question 12.
Find the constant b that makes g continuous on (-∞, ∞)
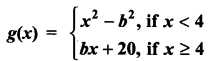
Solution:
Since g(x) is continuous,
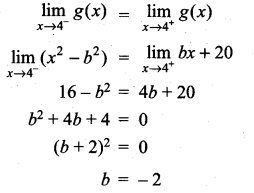
![]()
Question 13.
Consider the function f(x) = x sin \(\frac{\pi}{x}\). What value must we give f(0) in order to make the function continuous everywhere?
Solution:
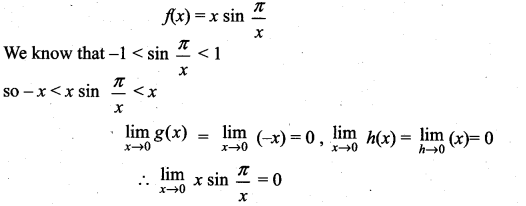
so to make the function f(x) is continuous at f(0) = 0
Question 14.
The function f(x) = \(\frac{x^{2}-1}{x^{3}-1}\) is not defined at x = 1. What value must we give f(1) in order to make f(x) continuous at x = 1?
Solution:
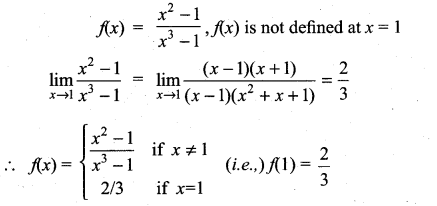
Question 15.
State how continuity is destroyed at x = x0 for each of the following graphs.
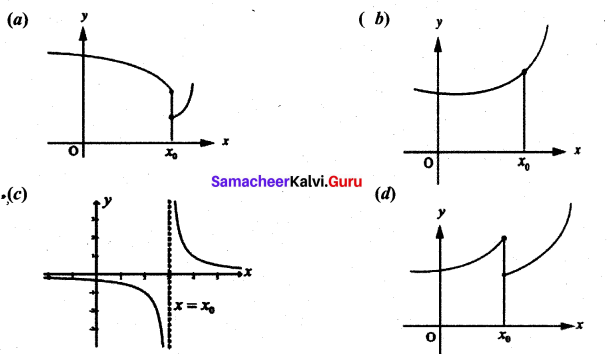
Solution:
