Samacheer Kalvi Class 11th Physics Solutions Chapter 11 Waves Questions and Answers. Aids you to prepare all the topics in it effectively. You need not worry about the accuracy of the Tamilnadu State Board Solutions for Class 11th Chapter 11 Waves as they are given adhering to the latest exam pattern and syllabus guidelines. Enhance your subject knowledge by preparing from the Chapterwise Samacheer Kalvi 11th Physics Solutions clarify your doubts on the corresponding topics.
Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 11 Waves
Kick start your preparation by using our online resource Samacheer Kalvi Class 11th Physics Solutions Chapter 11 Waves Questions and Answers. You can even download the Tamilnadu State Board Solutions for Class 11th Chapter 11 Waves free of cost through the direct links available on our page. Clear your queries and understand the concept behind them in a simple manner. Simply tap on the concept you wish to prepare in the chapter and go through it.
Samacheer Kalvi 11th Physics Waves Textual Evaluation Solved
Samacheer Kalvi 11th Physics Waves Multiple Choice Questions
Question 1.
A student tunes his guitar by striking a 120 Hertz with a tuning fork, and simultaneously plays the 4th string on his guitar. By keen observation, he hears the amplitude of the combined sound oscillating thrice per second. Which of the following frequencies is the most likely the frequency of the 4th string on his guitar?
(a) 130
(b) 117
(c) 110
(d) 120
Answer:
(b) 117
Question 2.
A transverse wave moves from a medium A to a medium B. In medium A, the velocity of the transverse wave is 500 ms-1 and the wavelength is 5 m. The frequency and the wavelength of the wave in medium B when its velocity is 600 ms-1, respectively are
(a) 120 Hz and 5 m
(b) 100 Hz and 5 m
(c) 120 Hz and 6 m
(d) 100 Hz and 6 m
Answer:
(d) 100 Hz and 6 m
Question 3.
For a particular tube, among six harmonic frequencies below 1000 Hz, only four harmonic frequencies are given : 300 Hz, 600 Hz, 750 Hz and 900 Hz. What are the two other frequencies missing from this list?
(a) 100 Hz, 150 Hz
(b) 150 Hz, 450 Hz
(c) 450 Hz, 700 Hz
(d) 700 Hz, 800 Hz
Answer:
(b) 150 Hz, 450 Hz
Hint:
If the tube is open at both ends so the harmonic frequencies are based on 150 Hz.
1st = 150 Hz ; 2nd = 300 Hz ; 3rd = 450 Hz ; 4th = 600 Hz ; 5th = 750 Hz ; 6th = 900 Hz
The above frequencies the missing frequency in the list 150 Hz, 450 Hz
Question 4.
Which of the following options is correct?

Options for (1), (2) and (3), respectively are
(a) (B), (C) and (A)
(b) (C), (A) and (B)
(c) (A), (B) and (C)
(d) (B), (A) and (C)
Answer:
(a) (B), (C) and (A)
Question 5.
Compare the velocities of the wave forms given below, and choose the correct option.

where, vA, vB, vC and vD are velocities given in (A), (B), (C) and (D), respectively.
(a) VA > VB > VD > VC
(b) VA < VB < VD < VC
(c) VA = VB = VD = VC
(d) VA > VB = VD > VC
Answer:
(c) VA = VB = VD = VC
Question 6.
A sound wave whose frequency is 5000 Hz travels in air and then hits the water surface. The ratio of its wavelengths in water and air is …….
(a) 4.30
(b) 0.23
(c) 5.30
(d) 1.23
Answer:
(a) 4.30
Hint.
Frequency of sound, f = 5000 Hz

Question 7.
A person standing between two parallel hills fires a gun and hears the first echo after t1 sec and the second echo after t2 sec. The distance between the two hills is …..

Answer:
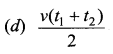
Hint:

Question 8.
An air column in a pipe which is closed at one end, will be in resonance with the vibrating body of frequency 83 Hz. Then the length of the air column is ………
(a) 1.5 m
(b) 0.5 m(c) 1.0 m
(d) 2.0 m
Answer:
(c) 1.0 m
Hint:

Velocity of sound in air y = 343 ms-1
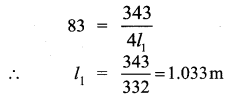
Question 9.
The displacement y of a wave travelling in the x direction is given by ![]() where x and y are measured in metres and t in second. The speed of the wave is ………
where x and y are measured in metres and t in second. The speed of the wave is ………
(a) 150 ms-1
(b) 300 ms-1
(c) 450 ms-1
(d) 600 ms-1
Answer:
(a) 150 ms-1
Hint:

Question 10.
Consider two uniform wires vibrating simultaneously in their fundamental notes. The tensions, densities, lengths and diameter of the two wires are in the ratio 8 : 1, 1 : 2, x : y and 4 : 1 respectively. If the note of the higher pitch has a frequency of 360 Hz and the number of beats produced per second is 10, then the value of x : y is ……….
(a) 36 : 35
(b) 35 : 36
(c) 1 : 1
(d) 1 : 2
Answer:
(a) 36 : 35
Question 11.
Which of the following represents a wave?
(a) (x – vt)3
(b) x(x + vt)
(c) \(\frac{1}{(x+v t)}\)
(d) sin (x + vt)
Answer:
(d) sin (x + vt)
Question 12.
A man sitting on a swing which is moving to an angle of 60° from the vertical is blowing a whistle which has a frequency of 2.0 k Hz. The whistle is 2.0 m from the fixed support point of the swing. A sound detector which detects the whistle sound is kept in front of the swing. The maximum frequency the sound detector detected is …….
(a) 2.027 kHz
(b) 1.947 kHz
(c) 9.74 kHz
(d) 1.011 kHz
Answer:
(a) 2.027 kHz
Question 13.
Let. y = \(\frac{1}{1+x^{2}}\) at t = 0s be the amplitude of the wave propagating in the positive x-direction. At t = 2s, the amplitude of the wave propagating becomes 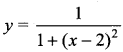 . Assume that the shape of the wave does not change during propagation. The velocity of the wave is …..
. Assume that the shape of the wave does not change during propagation. The velocity of the wave is …..
(a) 0.5 ms-1
(b) 1.0 ms-1
(c) 1.5 ms-1
(d) 2.0 ms-1
Answer:
(b) 1.0 ms-1
Hint.
The general expression y in terms of x
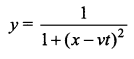
The shape of wave does not change, also wave move in 2 sec, 2m in positive ‘x’ direction. So, wave moves 2m in 2 sec.
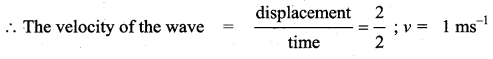
Question 14.
A uniform rope having mass m hangs vertically from a rigid support. A transverse wave pulse is produced at the lower end. Which of the following plots shows the correct variation of speed v with height h from the lower end?
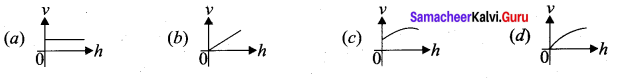
Answer:
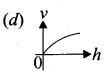
Question 15.
An organ pipe A closed at one end is allowed to vibrate in its first harmonic and another pipe B open at both ends is allowed to vibrate in its third harmonic. Both A and B are in resonance with a given tuning fork. The ratio of the length of A and B is …….

Answer:
(c) \(\frac{1}{6}\)
Hint:
(c) \(\frac{1}{6}\)
Samacheer Kalvi 11th Physics Waves Short Answer Questions
Question 1.
What is meant by waves?
Answer:
A disturbance that carries energy and momentum from one point in space to another point in space without the transfer of medium is known as a wave.
Question 2.
Write down the types of waves.
Answer:
Waves can be classified into two types:
(a) Transverse waves
(b) Longitudinal waves
Question 3.
What are transverse waves? Give one example.
Answer:
The direction of vibration of particles in a medium is perpendicular to the direction of propagation of the wave.
Example: Light (electromagnetic waves).
Question 4.
What are longitudinal waves? Give one example.
Answer:
In longitudinal wave motion, the constituent of the medium oscillate or vibrate about their mean positions in a direction parallel to the direction of propagation (direction of energy transfer) of waves.
Example: Sound waves travelling in air.
Question 5.
Define wavelength.
Answer:
The distance between two consecutive crests or troughs is known as wavelength, λ.
Question 6.
Write down the relation between frequency, wavelength and velocity of a wave.
Answer:

Question 7.
What is meant by the interference of waves?
Answer:
Interference is a phenomenon in which two waves superimpose to form a resultant wave of greater, lower, or the same amplitude.
Question 8.
Explain the beat phenomenon.
Answer:
When we superimpose two or more waves with slightly different frequencies then a sound of periodically varying amplitude at a point is observed. This phenomenon is known as beats.
Question 9.
Define intensity of sound and loudness of sound.
Answer:
- The loudness of sound is defined as “the degree of the sensation of sound produced in the ear or the perception of sound by the listener”.
- The intensity of sound is defined as “the sound power transmitted per unit area taken normal to the propagation of the sound wave”.
Question 10.
Explain Doppler Effect.
Answer:
When the source and the observer are in relative motion with respect to the medium in which sound propagates, the frequency of the sound wave observed is different from the frequency of the source. This phenomenon is called Doppler effect.
Question 11.
Explain red shift and blue shift in Doppler Effect.
Answer:
If the spectral lines of the star are found to shift towards red end of the spectrum (called as red shift) then the star is receding away from the Earth. Similarly, if the spectral lines of the star are found to shift towards the blue end of the spectrum (called as blue shift) then the star is approaching Earth.
Question 12.
What is meant by end correction in resonance air column apparatus?
Answer:
The antinodes are not exactly formed at the open end, we have to include a correction, called end correction e, by assuming that the antinode is formed at some small distance above the open end. Including this end correction, the first resonance is
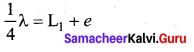
Again taking end correction into account, we have
![]()
Question 13.
Sketch the function Y = x + a. Explain your sketch
Answer:
When a = 0, y = x
when a = 1; x = 1: y = 1 + 1 = 2
when a = 2; x = 2; y = 2 + 2 = 4
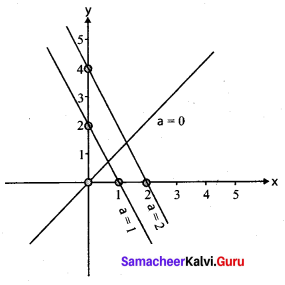
Explanation: This implies, when increasing the value of a, the line shifts towards right side at a = 0, and line shifts towards left side at a = 1, 2, ….For a = vt, y = x – vt satisfies the differential equation. Though this function satisfies the differential equation, it is not finite for all values of x and t. Hence it does not represent waves.
Question 14.
Write down the factors affecting the velocity of sound in gases.
Answer:
- Effect of pressure: Speed of sound is independent of pressure for a fixed temperature.
- Effect of temperature: Speed of sound varies directly to the square root of temperature in kelvin. Speed of sound in air increases by 0.61 ms-1 per degree Celcius rise in temperature.
- Effect of density: The velocity of sound in a gas is inversely proportional to the square root of the density of the gas.
- Effect of moisture (humidity): Speed of sound increases with rising in humidity.
- Effect of wind: In the direction along the wind blowing, the speed of sound to wind blowing, the speed of sound decreases.
Question 15.
What is meant by an echo? Explain.
Answer:
Echo: An echo is a repetition of sound produced by the reflection of sound waves from a wall, mountain or other obstructing surfaces.
Explanation: The speed of sound in air at 20°C is 344 m s-1. If we shout at a wall which is at 344 m away, then the sound will take 1 second to reach the wall. After reflection, the sound will take one more second to reach us. Therefore, we hear the echo after two seconds. Scientists have estimated that we can hear two sounds properly if the time gap or time interval between each sound is \(\left(\frac{1}{10}\right)^{\text {th }}\) of a second (persistence of hearing) i.e., 0.1 s. Then,
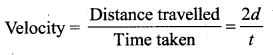
2d= 344 × 0.1 = 34.4m ;d= 17.2m
The minimum distance from a sound-reflecting wall to hear an echo at 20°C is 17.2 meter.
Samacheer Kalvi 11th Physics Waves Long Answer Questions
Question 1.
Discuss how ripples are formed in still water.
Answer:
Suppose we drop a stone in a trough of still water, it can be seen disturbance produced at the place where the stone strikes the water surface. It is found that this disturbance spreads out (diverges out) in the form of concentric circles of ever-increasing radii (ripples) then they strike the boundary of the trough.
It is because some of the kinetic energy of the stone is transmitted to the water molecules on the surface. Actually, the particles of the water (medium) themselves do not move outward with the disturbance. This can be observed by keeping a paper strip on the water surface. The strip moves up and down when the disturbance (wave) passes on the water surface. This shows that the water molecules only undergo vibratory motion about their mean positions.
Question 2.
Briefly explain the difference between travelling waves and standing waves.
Answer:

Question 3.
Show that the velocity of a travelling wave produced in a string is v =\(\sqrt{\frac{\mathrm{T}}{\mu}}\)
Answer:
Velocity of transverse waves in a stretched string: Let us compute the velocity of transverse travelling waves on a string. When a jerk is given at one end (left end) of the rope, the wave pulses move towards right end with a velocity v. This means that the pulses move with a velocity v with respect to an observer who is at rest frame. Suppose an observer also moves with same velocity v in the direction of motion of the wave pulse, then that observer will notice that the wave pulse is stationary and the rope is moving with pulse with the same velocity v. Consider an elemental segment in the string. Let A and B be two points on the string at an instant of time. Let dl and dm be the length and mass of the elemental string, respectively. By definition, linear mass density, μ is

The elemental string AB has a curvature which looks like an arc of a circle with centre at O, radius R and the arc subtending an angle θ at the origin O. The angle θ can be written in terms of arc length and radius as θ = \(\frac{d l}{R}\). The centripetal acceleration supplied by the tension in the string is

Then, centripetal force can be obtained when mass of the string (dm) is included in equation (3)

The centripetal force experienced by elemental string can be calculated by substituting equation (2) in equation (4) we get
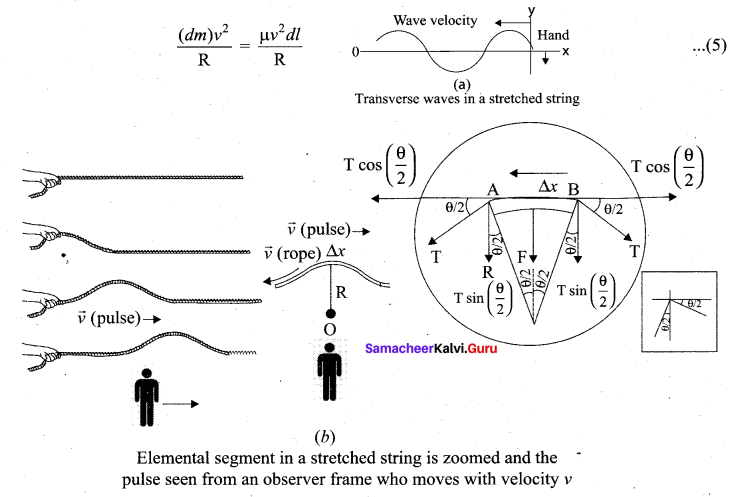
The tension T acts along the tangent of the elemental segment of the string at A and B. Since the arc length is very small, variation in the tension force can be ignored. We can resolve T into horizontal component T cos \(\left(\frac{\theta}{2}\right)\) and vertical component T sin \(\left(\frac{\theta}{2}\right)\) The horizontal component at A and B are equal in magnitude but opposite in direction; therefore, they cancel each other. Since the elemental arc length AB is taken to be very small, the vertical components at A and B appears to acts Vertical towards the centre of the arc and hence, they add up. The net radial force Fr is
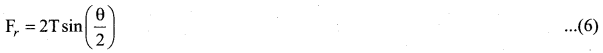
Since the amplitude of the wave is very small when it is compared with the length of the spring, the sine of small angle is approximated as sin \(\left(\frac{\theta}{2}\right) \approx \frac{\theta}{2}\). Hence equation (6) can be written as

Applying Newton’s second law to the elemental string in the radial direction, under equilibrium, the radial component of the force is equal to the centripetal force. Hence equating equation (5)

Question 4.
Describe Newton’s formula for the velocity of sound waves in the air and also discuss Laplace’s correction.
Answer:
Newton’s formula for the speed of sound waves in air: Sir Isaac Newton assumed that when sound propagates in air, the formation of compression and rarefaction takes place in a very slow manner so that the process is isothermal in nature. That is, the heat produced during compression (pressure increases, volume decreases), and heat lost during rarefaction (pressure decreases, volume increases) occur over a period of time such that the temperature of the medium remains constant. Therefore, by treating the air molecules to form an ideal gas, the changes in pressure and volume obey Boyle’s law, Mathematically
PV = constant …(1)
Differentiating equation (1), we get
![]()
where, BT is an isothermal bulk modulus of air. Substituting equation (2) in equation the speed of sound in air is

Since P is the pressure of air whose value at NTP (Normal Temperature and Pressure) is 76 cm of mercury, we have
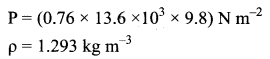
Here ρ is density of air, then the speed of sound in air at Normal Temperature and Pressure (NTP) is
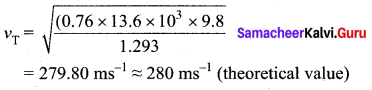
But the speed of sound in air at 0°C is experimentally observed as 332 m s-1 which is close upto 16% more than the theoretical value (Percentage error is ![]() ). This error is not small.
). This error is not small.
Laplace’s correction: In 1816, Laplace satisfactorily corrected this discrepancy by assuming that when the sound propagates through a medium, the particles oscillate very rapidly such that the compression and rarefaction occur very fast. Hence the exchange of heat produced due to compression and cooling effect due to rarefaction do not take place, because, air (medium) is a bad conductor of heat. Since temperature is no longer considered as a constant here, sound propagation is an adiabatic process. By adiabatic considerations, the gas obeys Poisson’s law (not Boyle’s law as Newton assumed), which is

Since air contains mainly, nitrogen, oxygen, hydrogen etc, (diatomic gas), we take γ = 1.47.
![]()
Question 5.
Write short notes on reflection of sound waves from plane and curved surfaces. Reflection of sound through the plane surface
Answer:
When the sound waves hit the plane wall, they bounce off in a manner similar to that of light. Suppose a loudspeaker is kept at an angle with respect to a wall (plane surface), then the waves coming from the source (assumed to be a point source) can be treated as spherical wavefronts (say, compressions moving like a spherical wavefront). Therefore, the reflected wavefront on the plane surface is also spherical, such that its centre of curvature (which lies on the other side of the plane surface) can be treated as the image of the sound source (virtual or imaginary loudspeaker) which can be assumed to be at a position behind the plane surface.
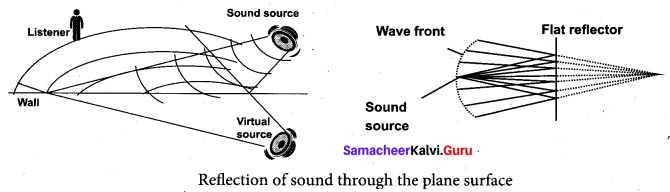
Reflection of sound through the curved surface: The behaviour of sound is different when – it is reflected from different surfaces-convex or concave or plane. The sound reflected from a convex surface is spread out and so it is easily attenuated and weakened. Whereas, if it is reflected from the concave surface it will converge at a point and this can be easily amplified. The parabolic reflector (curved reflector) which is used to focus the sound precisely to a point is used in designing the parabolic mics which are known as high directional microphones.
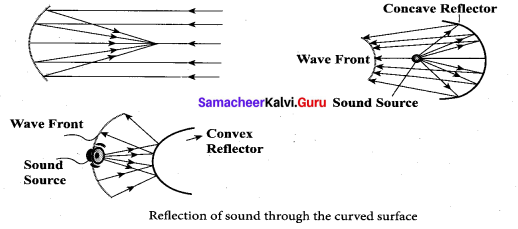
We know that any surface (smooth or rough) can absorb sound. For example, the sound produced in a big hall or auditorium or theatre is absorbed by the walls, ceilings, floor, seats etc. To avoid such losses, a curved soundboard (concave board) is kept in front of the speaker, so that the board reflects the sound waves of the speaker towards the audience. This method will minimize the spreading of sound waves in all possible directions in that hall and also enhances the uniform distribution of sound throughout the hall. That is why a person sitting at any position in that hall can hear the sound without any disturbance.
Question 6.
Briefly explain the concept of the superposition principle.
Answer:
Superposition Principle: When a jerk is given to a stretched string which is tied at one end, a wave pulse is produced and the pulse travels along the string. Suppose two persons holding the stretched string on either side give a jerk simultaneously, then these two wave pulses move towards each other, meet at some point and move away from each other with their original identity. Their behaviour is very different only at the crossing/meeting points; this behaviour depends on whether the two pulses have the same or different shapes.
When the pulses have the same shape, at the crossing, the total displacement is the algebraic sum of their individual displacements and hence its net amplitude is higher than the amplitudes of the individual pulses. Whereas, if the two pulses have the same amplitude but shapes are 180° out of phase at the crossing point, the net amplitude vanishes at that point and the pulses will recover their identities after crossing.
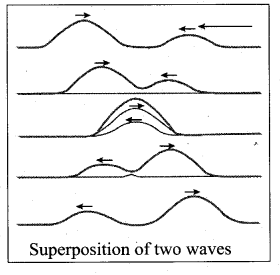
Only waves can possess such a peculiar property and it is called the superposition of waves. This means that the principle of superposition explains the net behaviour of the waves when they overlap. Generalizing to any number of waves i.e., if two are more waves in a medium move simultaneously, when they overlap, their total displacement is the vector sum of the individual displacements. We know that the waves satisfy the wave equation which is a linear second-order homogeneous partial differential equation in both space coordinates and time. Hence, their linear combination (often called as a linear superposition of waves) will also satisfy the same differential equation. To understand mathematically, let us consider two functions which characterize the displacement of the waves, for example,
y1 = A1 sin (kx – ωt) and y2= A2 cos (kx – ωt)
Since, both y1 and y2 satisfy the wave equation (solutions of wave equation) then their algebraic sum
y = y1 + y2
also satisfies the wave equation. This means the displacements are additive. Suppose we multiply y1 and y2 with some constant then their amplitude is scaled by that constant Further, if C1 and C2 are used to multiply the displacements y1 and y2, respectively, then, their net displacement y is
C = C1y1 + C2y2
This can be generalized to any number of waves. In the case of n such waves in more than one dimension the displacements are written using vector notation. Here, the net displacement \(\vec{y}\) is
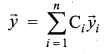
The principle of superposition can explain the following:
- Space (or spatial) Interference (also known as Interference)
- Time (or Temporal) Interference (also known as Beats)
- Concept of stationary waves
Waves that obey the principle of superposition are called linear waves (amplitude is much smaller than their wavelengths). In general, if the amplitude of the wave is not small then they are called non-linear waves. These violate the linear superposition principle, e.g., laser. In this chapter, we will focus our attention only on linear waves.
Question 7.
Explain how the interference of waves is formed.
Answer:
Consider two harmonic waves having identical frequencies, constant phase difference cp and same wave form (can be treated as coherent source), hut having amplitudes A1 and A2, then
![]()
Suppose they move simultaneously in a particular direction, then interference occurs (i.e., overlap of these two waves). Mathematically
y = y1 + y2 …. (3)
Therefore, substituting equation (1) and equation (3) in equation (3), we get
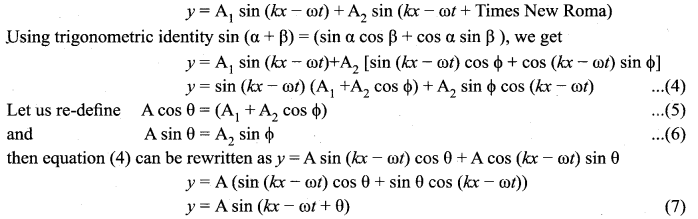
By squaring and adding equation (5) and equation (6), we get
![]()
Since intensity is square of the amplitude (I = A2), we have
![]()
This means the resultant intensity at any point depends on the phase difference at that point.
(a) For constructive interference:
When crests of one wave overlap with crests of another wave, their amplitudes will add up and we get constructive interference. The resultant wave has a larger amplitude than the individual waves as shown in figure (a).

The constructive interference at a point occurs if there is maximum intensity at that point, which means that
![]()
This is the phase difference in which two waves overlap to give constructive interference. Therefore, for this resultant wave,
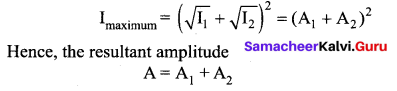
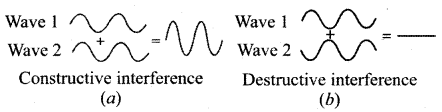
(b) For destructive interference: When the trough of one wave overlaps with the crest of another wave, their amplitudes “cancel” each other and we get destructive interference as shown in figure (b). The resultant amplitude is nearly zero. The destructive interference occurs if there is minimum intensity at that point, which means cos φ = – 1 ⇒ φ = π, 3π, 5π,… = (2n – 1) K, where n = 0, 1, 2, …. i.e. This is the phase difference in which two waves overlap to give destructive interference. Therefore,
![]()
Hence, the resultant amplitude A = |A1 – A2|
Question 8.
Describe the formation of beats.
Answer:
Formation of beats: When two or more waves superimpose each other with slightly different frequencies, then a sound of periodically varying amplitude at a point is observed. This phenomenon is known as beats. The number of amplitude maxima per second is called beat frequency. If we have two sources, then their difference in frequency gives the beat frequency. Number of beats per second
n = |f1 – f2|
Question 9.
What are stationary waves?. Explain the formation of stationary waves and also write down the characteristics of stationary waves.
Answer:
Explanation of stationary waves: When the wave hits the rigid boundary it bounces back to the original medium and can interfere with the original waves. A pattern is formed, which are known as standing waves or stationary waves.
Explanation: Consider two harmonic progressive waves (formed by strings) that have the same amplitude and same velocity but move in opposite directions. Then the displacement of the first wave (incident wave) is
y1 = A sin (kx – ωt) (waves move toward right) …(1)
and the displacement of the second wave (reflected wave) is
y2 = A sin (kx + ωt) (waves move toward left) …(2)
both will interfere with each other by the principle of superposition, the net displacement is
y = y1 + y2 …… (3)
Substituting equation (1) and equation (2) in equation (3), we get
y = A sin (kx – ωt) + A sin (kx + ωt) …(4)
Using trigonometric identity, we rewrite equation (4) as
y(x, t) = 2A cos (ωt) sin (kx) …(5)
This represents a stationary wave or standing wave, which means that this wave does not move either forward or backward, whereas progressive or travelling waves will move forward or backward. Further, the displacement of the particle in equation (5) can be written in more compact form,
y(x, t) = A’ cos (ωt)
where, A’ = 2A sin (foe), implying that the particular element of the string executes simple harmonic motion with amplitude equals to A’. The maximum of this amplitude occurs at positions for which
![]()
where m takes half-integer or half-integral values. The position of maximum amplitude is known as an antinode.
Expressing wave number in terms of wavelength, we can represent the anti-nodal positions as

The distance between two successive antinodes can be computed by
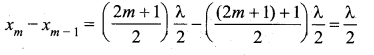
Similarly, the minimum of the amplitude A’ also occurs at some points in the space, and these points can be determined by setting
sin (kx) = 0 ⇒ kx = 0, π, 2π, 3π, … = nπ
where n takes integer or integral values. Note that the elements at these points do not vibrate (not move), and the points are called nodes. The nth nodal positions is given by,

Characteristics of stationary waves:
- Stationary waves are characterized by the confinement of a wave disturbance between two rigid boundaries. This means, the wave does not move forward or backward in a medium (does not advance), it remains steady at its place. Therefore, they are called “stationary waves or standing waves”.
- Certain points in the region in which the wave exists have maximum amplitude, called as anti-nodes and at certain points, the amplitude is minimum or zero, called as nodes.
- The distance between two consecutive nodes (or) anti-nodes is \(\frac{\lambda}{2}\)
- The distance between a node and its neighbouring anti-node is \(\frac{\lambda}{4}\)
- The transfer of energy along the standing wave is zero.
Question 10.
Discuss the law of transverse vibrations in stretched strings.
Answer:
Laws of transverse vibrations in stretched strings: There are three laws of transverse vibrations of stretched strings which are given as follows:
(i) The law of length: For a given wire with tension T (which is fixed) and mass per unit length µ (fixed) the frequency varies inversely with the vibrating length. Therefore,
![]()
⇒ l × f = C, where C is a constant
(ii) The law of tension: For a given vibrating length l (fixed) and mass per unit length p , (fixed) the frequency varies directly with the square root of the tension T,
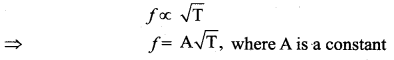
(iii) The law of mass: For a given vibrating length l (fixed) and tension T (fixed) the frequency varies inversely with the square root of the mass per unit length µ,

Question 11.
Explain the concepts of the fundamental frequency, harmonics and overtones in detail. Fundamental frequency and overtones in detail.
Answer:
Fundamental frequency and overtones: Let us now keep the rigid boundaries at x = 0 and x = L and produce standing waves by wiggling the string (as in plucking strings in a guitar). Standing waves with a specific wavelength are produced. Since, the amplitude must vanish at the boundaries, therefore, the displacement at the boundary must satisfy the following conditions
x(x = 0, t) = 0 and y(x = L, t) = 0
Since, the nodes formed at a distance \(\frac{\lambda_{n}}{2}\) apart, we have \(n\left(\frac{\lambda_{n}}{2}\right)=\mathrm{L}\), where n is an integer, L is the length between the two boundaries and λn is the specific wavelength that satisfy the specified boundary conditions. Hence,
![]()
Therefore, not all wavelengths are allowed. The (allowed) wavelengths should fit with the specified boundary conditions, i.e., for n = 1, the first mode of vibration has specific wavelength λ1 = 2L. Similarly for n = 2, the second mode of vibration has specific wavelength
![]()
For n = 3, the third mode of vibration has specific wavelength
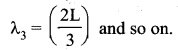
The frequency of each mode of vibration (called natural frequency) can be calculated.

The lowest natural frequency is called the fundamental frequency.
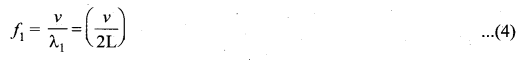
The second natural frequency is called the first overtone.
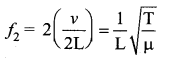
The third natural frequency is called the second overtone.
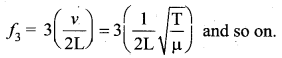
Therefore, the nth natural frequency can be computed as integral (or integer ) multiple of the fundamental frequency, i.e.,
fn = nf1 where n is an integer …(5)
If natural frequencies are written as an integral multiple of fundamental frequencies, then the frequencies are called harmonics. Thus, the first harmonic is f1 = f1 (the fundamental frequency is called first harmonic), the second harmonic is f2 = 2f1, the third harmonic is f3 = 3f1 etc.
Question 12.
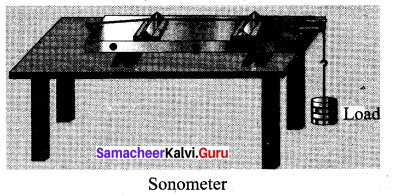
What is a sonometer? Give its construction and working. Explain how to determine the frequency of tuning fork using a sonometer.
Answer:
Stationary waves in sonometer: Sono means sound related, and sonometer implies sound-related measurements.
It is a device for demonstrating the relationship between the frequency of the sound produced in the transverse standing wave in a string, and the tension, length and mass per unit length of the string. Therefore, using this device, we can determine the following quantities:
- the frequency of the tuning fork or frequency of alternating current
- the tension in the string
- the unknown hanging mass
Construction: The sonometer is made up of a hollow box which is one meter long with a uniform metallic thin string attached to it. One end of the string is connected to a hook and the other end is connected to a weight hanger through a pulley as shown in the figure. Since only one string is used, it is also known as monochord. The weights are added to the free end of the wire to increase the tension of the wire. Two adjustable wooden knives are put over the board, and their positions are adjusted to change the vibrating length of the stretched wire.
Working: A transverse stationary or standing wave is produced and hence, at the knife edges P and Q, nodes are formed. In between the knife edges, anti-nodes are formed. If the length of the vibrating element is then
![]()
Let f be the frequency of the vibrating element, T the tension of in the string and p the mass per unit length of the string. Then using equation, we get

Let ρ be the density of the material of the string and d be the diameter of the string. Then the mass per unit length μ

Question 13.
Write short notes on intensity and loudness.
Answer:
Intensity and loudness: Consider a source and two observers (listeners). The source emits sound waves which carry energy. The sound energy emitted by the source is same regardless of whoever measures it, i.e., it is independent of any observers standing in that region. But the sound received by the two observers may be different; this is due to some factors like sensitivity of ears, etc. To quantify such thing, we define two different quantities known as intensity and loudness of sound.
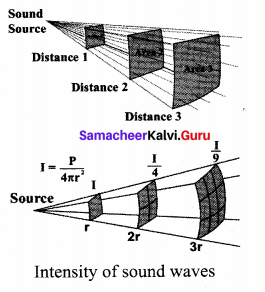
Intensity of sound: When a sound wave is emitted by a source, the energy is carried to all possible surrounding points. The average sound energy emitted or transmitted per unit time or per second is called sound power. Therefore, the intensity of sound is defined as “the sound power transmitted per unit area taken normal to the propagation of the sound wave ”.
For a particular source (fixed source), the sound intensity is inversely proportional to the square of the distance from the source.
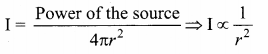
This is known as the inverse square law of sound intensity.
the power output does not depend on the observer and depends on the baby. Therefore, Loudness of sound: Two sounds with same intensities need not have the same loudness. For example, the sound heard during the explosion of balloons in a silent closed room is very loud when compared to the same explosion happening in a noisy market. Though the intensity of the sound is the same, the loudness is not. If the intensity of sound is increased then loudness also increases. But additionally, not only does intensity matter, the internal and subjective experience of “how loud a sound is” i.e., the sensitivity of the listener also matters here. This is often called loudness. That is, loudness depends on both intensities of sound wave and sensitivity of the ear (It is purely observer-dependent quantity which varies from person to person) whereas the intensity of sound does not depend on the observer. The loudness of sound is defined as “the degree of the sensation of sound produced in the ear or the perception of sound by the listener”.
Question 14.
Explain how overtones are produced in a:
(a) Closed organ pipe
(b) Open organ pipe
Answer:
(a) Closed organ pipes: Clarinet is an example of a closed organ pipe. It is a pipe with one end closed and the other end open. If one end of a pipe is closed, the wave reflected at this closed-end is 180° out of phase with the incoming wave. Thus there is no displacement of the particles at the closed end. Therefore, nodes are formed at the closed end, and anti-nodes are formed at open end.
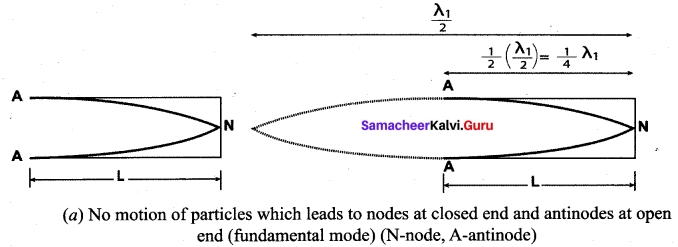
Let us consider the simplest mode of vibration of the air column called the fundamental mode. Anti-node is formed at the
open end and node at the closed end. From the figure, let L be the length of the tube and the wavelength of the wave produced. For the fundamental mode of vibration, we have,

which is called the fundamental note
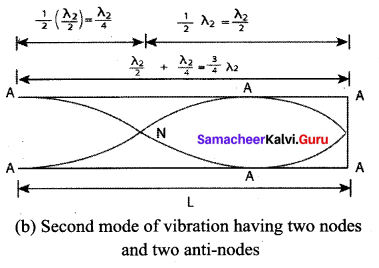
The frequencies higher than the fundamental frequency can be produced by blowing air strongly at the open end. Such frequencies are called overtones.
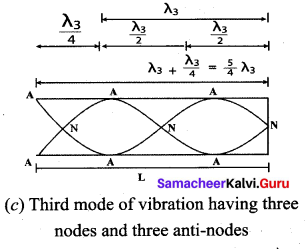
Figure (b) shows the second mode of vibration having two nodes and two antinodes,
is called the first overtone, since here, the frequency is three times the fundamental frequency it is called third harmonic.
Figure (c) shows the third mode of vibration having three nodes and three anti-nodes.
is called the second overtone, and since n = 5 here, this is called fifth harmonic. Hence, the closed organ pipe has only odd harmonics and the frequency of the nth harmonic is fn = (2n + 1)f1. Therefore, the frequencies of harmonics are in the ratio
f1 : f2 : f3 : f4 …… = 1 : 3 : 5 : 7 : …………… (3)
(b) Open organ pipes: Flute is an example of an open organ pipe. It is a pipe with both ends open. At both open ends, anti-nodes are formed. Let us consider the simplest mode of vibration of the air column called fundamental mode. Since anti-nodes are formed at the open end, a node is formed at the mid-point of the pipe.
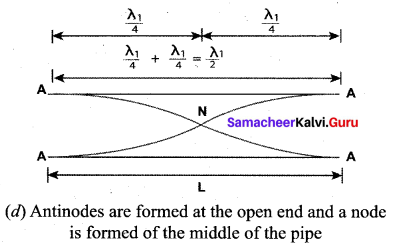
From figure (d), if L be the length of the tube, the wavelength of the wave produced is given by
![]()
The frequency of the note emitted is
![]()
which is called the fundamental note. The frequencies higher than the fundamental frequency can be produced by blowing air strongly at one of the open ends. Such frequencies are called overtones.
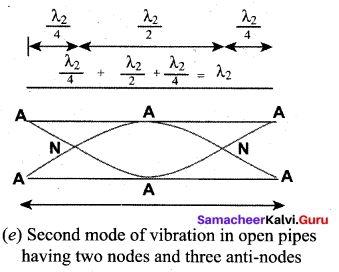
Figure (e) shows the second mode of vibration in open pipes. It has two nodes and three anti-nodes, and therefore,
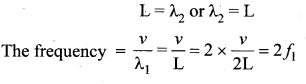
is called the first overtone. Since n = 2 here, it is called the second harmonic.
Figure (f) above shows the third mode of vibration having three nodes and four anti-nodes.
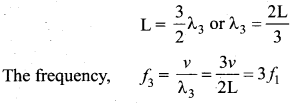
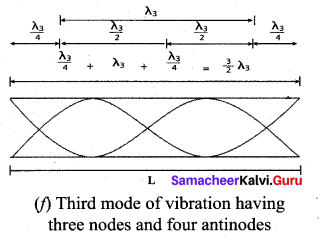
is called second overtone. Since n = 3 here, it is called the third harmonic.
Hence, the open organ pipe has all the – harmonics and the frequency of nth harmonic is fn = nf1. Therefore, the frequencies of harmonics are in the ratio
f1 : f2 : f3 : f4 … = 1 : 2 : 3 : 4 : … …(6)
Question 15.
How will you determine the velocity of sound using resonance air column apparatus?
Answer:
Resonance air column apparatus:
The resonance air column apparatus and first, second and third resonance The resonance air column apparatus is one of the simplest techniques to measure the speed of sound in air at room temperature. It consists of a cylindrical glass tube of one-meter length whose one end A is open and another end B is connected to the water reservoir R through a rubber tube as shown in the figure. This cylindrical glass tube is mounted on a vertical stand with a scale attached to it. The tube is partially filled with water and the water level can be adjusted by raising or lowering the water in reservoir R. The surface of the water will act as a closed erid and the other as the open end. Therefore, it behaves like a closed organ pipe, forming nodes at the surface of water and antinodes at the closed end.
When a vibrating tuning fork is brought near the open end of the tube, longitudinal waves are formed inside the air column. These waves move downward as shown in Figure, and reach the surfaces of water and get reflected and produce standing waves. The length of the air column is varied by changing the water level until a loud sound is produced in the air column. At this particular length, the frequency of waves in the air column resonates with the frequency of the tuning fork (natural frequency of the tuning fork). At resonance, the frequency of sound waves produced is equal to the frequency of the tuning fork. This will occur only when the length of air column is proportional to \(\left(\frac{1}{4}\right)^{t h}\) of the wavelength of the sound waves produced. Let the first resonance occur at length L1, then

But since the antinodes are not exactly formed at the open end, we have to include a correction, called end correction e, by assuming that the antinode is formed at some small distance above the open end. Including this end correction, the first resonance is
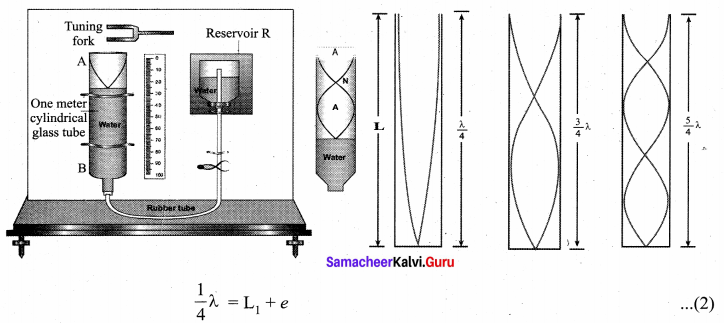
Now the length of the air column is increased to get the second resonance. Let L2 be the length at which the second resonance occurs. Again taking end correction into account, we have
![]()
In order to avoid end correction, let us make the difference of equation (3) and equation (2)
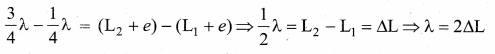
The speed of the sound in air at room temperature can be computed by using the formula
![]()
Further, to compute the end correction, we use equation (2) and equation (3), we get
Question 16.
What is meant by the Doppler effect? Discuss the following cases
(1) Source in motion and Observer at rest
(a) Source moves towards the observer
(b) Source moves away from the observer
(2) Observer in motion and Source at rest.
(a) Observer moves towards Source
(b) Observer resides away from the Source
(3) Both are in motion
(a) Source and Observer approach each other
(b) Source and Observer resides from each other
(c) Source chases Observer
(d) Observer chases Source
Answer:
Doppler Effect: When the source and the observer are in relative motion with respect to each other and to the medium in which sound propagates, the frequency of the sound wave observed is different from the frequency of the source. This phenomenon is called Doppler Effect.
1. Source in motion and the observer at rest
(a) Source moves towards the observer: Suppose a source S moves to the right (as shown in figure) with a velocity vs and let the frequency of the sound waves produced by the source be fs. We assume the velocity of sound in a medium is v.
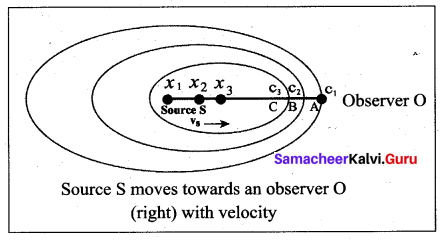
The compression (sound wavefront) produced by the source S at three successive instants of time are shown in the figure. When S is at position x1 the compression is at C1. When S is at position x2, the compression is at C2 and similarly for x3 and C3. Assume that if reaches the observer’s position A then at that instant C2 reaches point B and C3 reaches point C as shown in the figure. It is obvious to see that the distance between compressions C2 and C3 is shorter than the distance between C1 and C2.
This means the wavelength decreases when the source S moves towards the observer O (since sound travels longitudinally and wavelength is the distance between two consecutive compressions). But frequency is inversely related to wavelength and therefore, frequency increases.
Let λ be the wavelength of the source S as measured by the observer when S is at position x1 and λ’ be the wavelength of the source observed by the observer when S moves to position x2. Then the change in wavelength is ∆λ = λ – λ’ = vs t, where t is the time taken by the source to travel between x1 and x2. Therefore,

On substituting equation (2) in equation (1), we get 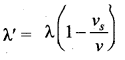

(b) Source moves away from the observer: Since the velocity here of the source is opposite in direction when compared to the case (a), therefore, changing the sign of the velocity of the source in the above case i.e, by substituting (vs ➝ – vs) in equation (1), we get

Using binomial expansion again, we get,

2. Observer in motion and source at rest:
(a) Observer moves towards Source:
Let us assume that the observer O moves towards the source S with velocity vo. The source S is at rest and the velocity of sound waves (with respect to the medium) produced by the source is v. From the figure, we observe that both vo and v are in opposite direction. Then, their relative velocity is vr = v + vo. The wavelength of the sound wave is \(\lambda=\frac{v}{f}\), which means the frequency observed by the observer O is f’ = \(\). Then
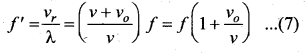
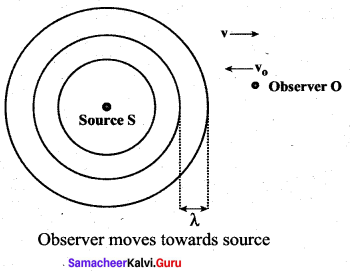
(b) Observer recedes away from the Source: If the observer O is moving away (receding away) from the source S, then velocity v0 and v moves in the same direction. Therefore, their relative velocity is vr = v – vr. Hence, the frequency observed by the observer O is
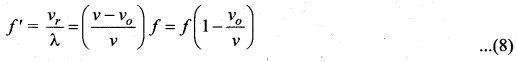
3. Both are in motion:
(a) Source and observer approach each other:

Let vs and vo be the respective velocities of source and observer approaching each other as shown in figure. In order to calculate the apparent frequency observed by the observer, as a simple calculation, let us have a dummy (behaving as observer or source) in between the source and observer. Since the dummy is at rest, the dummy (observer) observes the apparent frequency due to the approaching source as given in equation (3) as

At that instant of time, the true observer approaches the dummy from the other side. Since the source (true source) comes in a direction opposite to the true observer, the dummy (source) is treated as a stationary source for the true observer at that instant. Hence, an apparent frequency when the true observer approaches the stationary source (dummy source), from equation (7) is
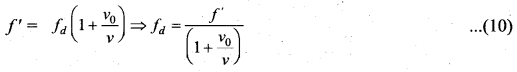
Since this is true for any arbitrary time, therefore, comparing equation (9) and equation (10), we get

(b) Source and observer resides from each other

Here, we can derive the result as in the previous case. Instead of a detailed calculation, by inspection from the figure, we notice that the velocity of the source and the observer each point in opposite directions with respect to the case in (a), and hence, we substitute (vs ➝ – vs) and (v0 ➝ – vo) in equation (11), and therefore, the apparent frequency observed by the observer when the source and observer recede from each other is

(c) Source chases the observer

Only the observer’s velocity is oppositely directed when compared to case (a).

(d) Observer chases the source

Only the source velocity is oppositely directed when compared to case (a). Therefore, substituting vs ➝ – vs in equation (12), we get
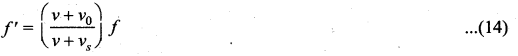
Samacheer Kalvi 11th Physics Waves Numerical Problems
Question 1.
The speed of a wave in a certain medium is 900 m/s. If 3000 waves passes over a certain point of the medium in 2 minutes, then compute its wavelength?
Answer:
Speed of the wave in medium v = 900 ms-1
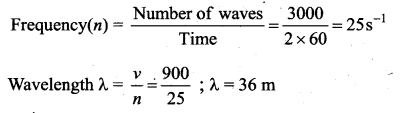
Question 2.
Consider a mixture of 2 mol of helium and 4 mol of oxygen. Compute the speed of sound in this gas mixture at 300 K.
Answer:
The mixture of helium and oxygen.
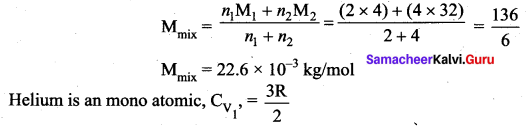

Question 3.
A ship in a sea sends SONAR waves straight down into the seawater from the bottom of the ship. The signal reflects from the deep bottom bed rock and returns to the ship after 3.5 s. After the ship moves to 100 km it sends another signal which returns back after 2s. Calculate the depth of the sea in each case and also compute the difference in height between two cases.
Answer:
Speed of SONAR waves in water c = 1500 ms-1
Time taken to reflect from the bottom of the sea, 2t = 3.5 sec
∴ t = 1.75 sec
Distance covered in forward and reflected backward (d1) = c × t
d2 = 1500 × 1.75 = 2625 m
After ship moves in a distance = 150 km
Time taken to reflect by the waves 2t = 2s
t = 1s
Distance covered by the waves (d2) = c × t = 1500 × 1 = 1500 m
The different between the height of two cases = 2625 – 1500
hdifference = 1124 m
Question 4.
A sound wave is transmitted into a tube as shown in figure. The sound wave splits into two waves at the point A which recombine at point B. Let R be the radius of the semicircle which is varied until the first minimum. Calculate the radius of the semi-circle if the wavelength of the sound is 50.0 m
Answer:
The sound travelling in the curved path distance = πR
L1 = πR
The sound travelling in the straight path distance = 2R
L2 = 2R
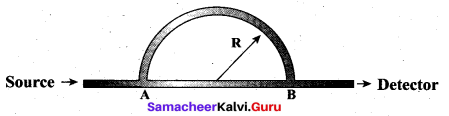
The path distance of straight and curved path AP = L1 – L2

Question 5.
N tuning forks are arranged in order of increasing frequency and any two successive tuning forks give n beats per second when sounded together. If the last fork gives double the frequency of the first (called an an octave), Show that the frequency of the first tuning fork is f = (N – 1)n.
Answer:
Total number of fork = N
The frequency of the 1st fork = f
The frequency of the last fork = 2f
∴ an = a + (n – 1)d
2f = f + (N – 1)n
2f – f = (N – 1)n
∴ f = (N – 1)n
Question 6.
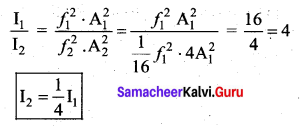
Let the source propagate a sound wave whose intensity at a point (initially) be I. Suppose we consider a case when the amplitude of the sound wave is doubled and the frequency is reduced to one-fourth. Calculate now the new intensity of sound at the same point?
Answer:
The intensity of sound wave (old) = I1
The amplitude of sound wave (A2) = 2A1
Frequency of the sound wave I2 = ?
![]()
Question 7.
Consider two organ pipes of same length in which one organ pipe is closed and another organ pipe is open. If the fundamental frequency of closed pipe is 250 Hz. Calculate the fundamental frequency of the open pipe.
Answer:
Fundamental frequency of closed organ pipe
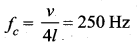
Fundamental frequency:f open organ pipe \(f_{o}=\frac{v}{2 l}=?\)

Question 8.
A police in a siren car moving with a velocity 20 ms– chases a thief who is moving in a car with a velocity v0 ms-1. The police car sounds at frequency 300 Hz, and both of them move towards a stationary siren of frequency 400 Hz. Calculate the speed in which thief is moving.
(Assume the thief does not observe any beat)
Answer:
Velocity of sound v = 330 ms-1
Velocity of car (vs ) = 20 ms-1
Frequency of car (f1) = 300 Hz
Frequency of stationary siren (f2) = 400 Hz
The speed of the thief (vo ) = ?

330 – vo = 413.325 + 1.2525vo
2.2525vo = – 83. 325
vo = – 36.99
∴ speed of the thief in moving = 36.99 ms-1
Question 9.
Consider the following function:
(a) y = x2 + 2 α tx
(b) y = (x + vt)2 which among the above function can be characterized as a wave?
Answer:
(a) y = x2 + 2 α tx. This expression is not a wave equation.
(b) y = (x + vt)2 . This expression is satisfies the wave equation.
Samacheer Kalvi 11th Physics Waves Conceptual Questions
Question 1.
Why is it that transverse waves cannot be produced in a gas? Can the transverse waves can be produced in solids and liquids?
Answer:
Transverse waves travel in the form of crests and through. They involve changes in the shape of the medium. As gas has no elasticity of shape, hence transverse waves cannot be produced in it. So, they can be transmitted through media which sustain shearing stress such as solids, strings and liquid surface.
Question 2.
Why is the roar of our national animal different from the sound of a mosquito?
Answer:
Both sounds travel at the speed of sound. The speed of sound varies according to the density and temperature of the air, but not according to the loudness of the sound,at least not for the levels of loudness we talking about here.
The roaring of the lion will be audible a lot further away, but that’s simply because it’s louder.
Question 3.
A sound source and listener are both stationary and a strong wind is blowing. Is there a Doppler effect?
Answer:
Yes, It does not matter whether the sound source or the transmission media are in motion, vibrations will be compressed in the direction of convergence and dilated in the direction of divergence.
Question 4.
In an empty room why is it that a tone sounds louder than in the room having things like furniture etc.
Answer:
Because in a furniture room will absorb the sound waves, hence there went be any echo. But in an empty room reflect the sound. Therefore there will be echo hence we hear sound louder.
Question 5.
How do animals sense the impending danger of hurricanes?
Answer:
Some animals are believed to be sensitive to be low-frequency sound waves emitted by hurricanes, they can also detect the slight drops in air and water pressure that signal a storm’s approach.
Question 6.
Is it possible to realize whether a vessel kept under the tap is about to fill with water?
Answer:
The frequency of the note produced by an air column is inversely proportional to its length. As the level of water is the vessel rises, the length of the air column above it decreases. It produces the sound of decreasing frequency, i.e., the sound becomes shorter. From the shrillness of sound, it is possible to realize whether the vessel is filled which water.
vmin = 11.71 ms-1
Samacheer Kalvi 11th Physics Waves Textual Evaluation Solved Additional Questions Solved
I. Choose the correct answer from the following:
Question 1.
Mechanical Waves
(a) are longitudinal only
(b) are transverse only
(c) can be both longitudinal and transverse.
(d) are neither longitudinal for transverse waves.
Answer:
(c) can be both longitudinal and transverse.
Question 2.
Sound whose frequency is 50 Hz?
(a) has a relatively short wavelength.
(b) has a relatively long wavelength
(c) is very loud
(d) is very intense
Answer:
(a) has a relatively short wavelength.
Question 3.
Sound travels fastest in …….
(a) Steel
(b) air
(c) water
(d) vaccum
Answer:
(a) steel
Question 4.
A boat at anchor is rocked by waves of velocity 25m/s, having crests 100 m apart. The boat bounches up once in every
(a) 4.0s
(b) 2500s
(c) 0.25s
(d) 75s
Answer:
(a) 4.0s
Hint:
λ = distance between crests = 100 m frequency v = \(\frac{25}{100}=\frac{1}{4} \mathrm{s}^{-1}\)
Therefore, the crests reach the boat once every 4 seconds.
Question 5.
Choose the correct statement:
(a) sound waves are transverse waves
(b) sound travels fastest through vaccum.
(c) sound travels faster in solids than in gases.
(d) sound travels faster in gases than in liquids.
Answer:
(c) sound travels faster in solids than in gases.
Question 6.
Transverse waves can propagate ……
(a) both in a gas and in a metal
(b) in a gas but not in a metal
(c) not in a gas but in a metal
(d) neither in a gas nor in a metal
Answer:
(a) not in a gas but in a metal.
Question 7.
The speed of the wave represented by y = A sin(ωt – kx) is ……..
(a) k/ω
(b) ω/k
(c) ωk
(d) 1/ωk
Answer:
(b) ω/k
Question 8.
The equation of a wave travelling in a string can be written as y = 3 cos {π(100t – x)} where y and x are in cm and t is in seconds. Then the value of wavelength is …….
(a) 100 cm
(b) 2 cm
(c) 50 cm
(d) 4 cm
Answer:
(b) 2 cm
Hint:
On comparing given equation with y = A cos (kx – ωt), we get
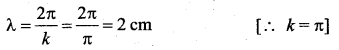
Question 9.
A wave of frequency 500 Hzhas a velocity 300 m/s. The distance between two nearest points which are 60° out of phase, is ……
(a) 0.2 m
(b) 0.1 m
(c) 0.4 m
(d) 0.5 m
Answer:
(a) 0.1 cm

Question 10.
The equation of a wave travelling on a string is 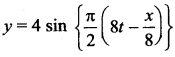 , where x, y are in cm and t in seconds. The velocity of the waves is ……..
, where x, y are in cm and t in seconds. The velocity of the waves is ……..
(a) 64 cm/s in – x direction
(b) 32 cm/s in – x direction
(c) 32 cm/s in +x direction
(d) 64 cm/s in + x direction
Answer:
(d) 64 cm/s in + x direction to S
![]()
Question 11.
The equation of a wave is 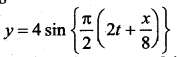 where y, x are in cm and t in seconds. The amplitude wavelength, velocity and frequency of the wave are, respectively, …….
where y, x are in cm and t in seconds. The amplitude wavelength, velocity and frequency of the wave are, respectively, …….
(a) 4 cm, 32 cm, 16 cm/s, 0.5 Hz
(b) 8 cm, 16 cm, 32 cm/s, 1.0 Hz
(c) 4 cm, 32 cm, 32 cm/s, 0.5 Hz
(d) 8 cm, 16 cm, 16 cm/s, 1.0 Hz
Answer:
(a) 4 cm, 32 cm, 16 cm/s, 0.5 Hz
Question 12.
The diagram shows the profile of a wave, which of the following pairs of points are in phase?
(a) A, B
(b) B, C
(c) B, D
(d) B, E
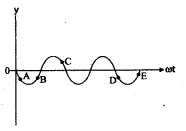
Answer:
(d) B, E
Question 13.
Ultrasonic waves are those waves which ………
(a) human beings cannot hear
(b) human beings can hear
(c) have high velocity
(d) have large amplitude
Answer:
(a) human beings cannot hear
Question 14.
A transverse wave of amplitude 0.5m, wavelength 1 m and frequency 2Hz is propogating in a string in the negative x-direction. The equation of this wave is ….
(a) y = 0.5 sin (2πx – 4πt)
(b) y = 0.5 sin (2πx + 4πt)
(c) y = 0.5 sin (πx – 2πt)
(d) y = 0.5 cos (kx – 2πt)
Answer:
(b) y = 0.5 sin (2πx + 4πt)
Hint:
y = A sin(kx + ωt)
Here A = 0.5 m
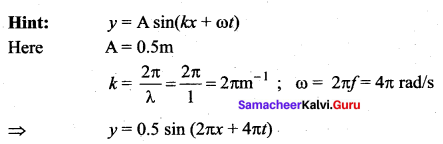
Question 15.
With the rise of temperature, the speed of sound in a gas ……..
(a) increases
(b) decreases
(c) remain the same
(d) may increase or decrease depending on the corresponding change in pressure.
Answer:
(a) increases
Question 16.
Speed of sound in a gas in proportional to …….
(a) square root of isothermal elasticity
(b) square root of adiabatic elasticity
(c) isothermal elasticity
(d) adiabatic elasticity
Answer:
(b) square root of adiabatic elasticity
Question 17.
The velocity of sound in are is not affected by change in the …….
(a) atmospheric pressure
(b) moisture content of air
(c) temperature of air
(d) composition of air
Answer:
(a) atmospheric pressure
Question 18.
A longitudinal wave is described by the equation y = y0 sin 2π (ft – x/λ). The maximum particle velocity is equal to four times the wave velocity if ……..
![]()
Answer:
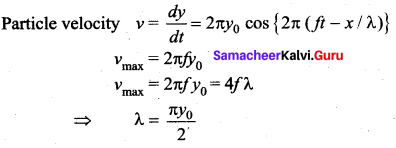
Question 19.
If v0 and v denote the sound velocity and the rms velocity of the molecules in a gas, then ……..

Answer:
![]()
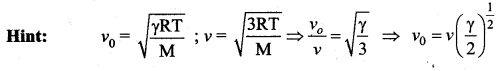
Question 20.
With the propagation of a longitudinal wave through a material medium, the quantities transferred in the direction of propagation are ……..
(a) energy, momentum and mass
(b) energy and momentum
(c) energy and mass
(d) energy
Answer:
(b) energy and momentum
Question 21.
If the amplitude of sound is doubled and the frequency reduced to one-fourth, the intensity will ………
(a) increase by a factor of 2
(b) decrease by a factor of 2
(c) decrease by a factor of 4
(d) remain unchanged
Answer:
(c) decrease by a factor of 4
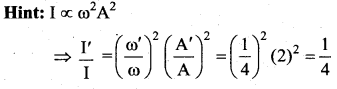
Question 22.
When a source of sound is in motion towards a stationary observer, the effect observed is
(a) increase in the velocity of sound only
(b) decrease in the velocity of sound only
(c) increase in frequency of sound only
(d) increase in both the velocity and the frequency of sound
Answer:
(c) increase in frequency of sound only
Question 23.
The apparent wavelength of the light from a star, moving away from the earth, is 0.01% more than its real wave length. The speed of the star with respect to the earth is ……
(a) 10 km/s
(b) 15 km/s
(c) 30 km/s
(d) 60 km/s
Answer:
(c) 30 km/s
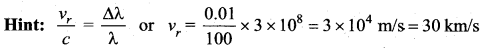
Question 24.
The frequency of a radar is 780 MHz. When it is reflected from an approaching aeroplane the opponent frequency is more than the actual frequency by 2.6 kHz. The speed of the aeroplane is ……
(a) 0.25 km/s
(b) 0.5 km/s
(c) 1.0 km/s
(d) 2.0 km/s
Answer:
(b) 0.5 km/s
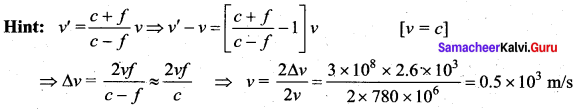
Question 25.
The temperature at which the speed of sound in air becomes double its value at 27°C is …….
(a) 54°C
(b) 327°C
(c) 927°C
(d) -123°C
Answer:
(c) 927°C
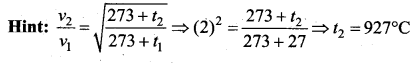
Question 26.
The equation of a transverse wave is given by y = 10 sin{π(0.01x – 2t)} where y and x are in cm and t is in seconds. Its frequency is …….
(a) 10 s-1
(b) 2 s-1
(c) 1 s-1
(d) 0.01 s-1
Answer:
(c) 1 s-1
Hint:
Comparing with the standard equation y = A sin(kx – ωt),
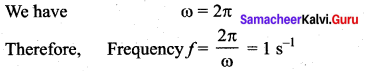
Question 27.
When sound waves travel from air to water, which of the following remains constant?
(a) velocity
(b) frequency
(c) wavelength
(d) all of these
Answer:
(b) frequency
Question 28.
The speed of sound in oxygen is 332 m/s at STP. The speed of sound in hydrogen at STP will be ……..
(a) 53/2 m/s
(b) 2546 m/s
(c) 1328 m/s
(d) 664 m/s
Answer:
(c) 1328 m/s

Question 29.
If va, vh, and vm are the speeds of sound in air, hydrogen and a metal at the same temperature, then ……..
(a) vh > va > vm
(b) vm > vh > va
(c) vh > vm > va
(d) va > vh > vm
Answer:
(b) vm > vh > va
Question 30.
Ultrasonic waves can be detected by ……
(a) telephone
(b) Hebb’s method
(c) Kundt’s tube
(d) Quincke’s tube
Answer:
(c) Kundt’s tube
Question 31.
The velocity of sound in a gas depends on ….
(a) Wavelength only
(b) density and elasticity of gas
(c) intensity only
(d) amplitude and frequency
Answer:
(b) density and elasticity of gas
Question 32.
When sound waves travel from air to water, which of these remains constant?
(a) velocity
(b) wavelength
(c) frequency
(d) all the above
Answer:
(c) frequency
Question 33.
When a wave goes from one medium to another, there is a change in
(a) velocity
(b) amplitude
(c) wavelength
(d) all the above
Answer:
(d) all the above
Question 34.
The equation of a sound wave is y = 0.0015 sin (62.8x + 316t). Find the wave length of the above ……
(a) 0.2 units
(b) 0.3 units
(c) 0.1 units
(d) 0.15 units
Answer:
(c) 0.1 units
![]()
Question 35.
Red shift is an illustration of ……….
(a) low temperature emission
(b) high frequency absorption
(c) Doppler effect
(d) Same unknown Phenomenon.
Answer:
(c) Doppler effect
Question 36.
The ratio of the velocity of sound in a monatomic gas to that in a triatomic gas having same molar mass, under similar conditions of temperature and pressure, is ………
(a) 1.12
(6) 1.25
(c) 1.50
(d) 1.6
Answer:
(a) 1.12
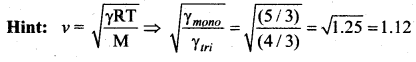
Question 37.
Doppler shift in frequency does not depend upon …….
(a) the actual frequency of the wave
(b) the velocity of the source from the listener.
(c) the velocity of the source.
(d) the velocity of the observer.
Answer:
(b) the velocity of the source from the listener.
Question 38.
If the density of oxygen is 16 times that of hydrogen, what will be the ratio of the velocities of sound in them?
(a) 1 : 4
(b) 4 : 1
(c) 2 : 1
(d) 1 : 16
Answer:
(a) 1 : 4
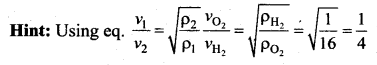
Question 39.
Pitch of sound depends on ……
(a) frequency
(b) wavelength
(c) amplitude
(d) speed
Answer:
(a) frequency
Question 40.
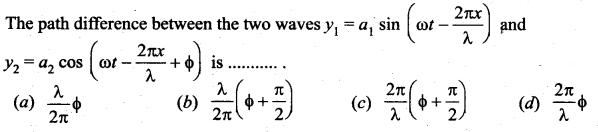
Answer:
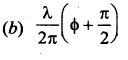
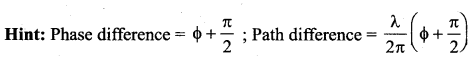
Question 41.
Which of the following equations represents a wave?
(a) y = A(ωt – kx)
(b) y = A sin ωt
(c) y = A cos kx
(d) y = A sin (at – bx + c)
Answer:
(d) y = A sin (at -bx + c)
Question 42.
A wave travels in a medium according to the equation of displacement given by y(x, t) = 0.03 sin{π(2t – 0.01 x)} where y and x are in metres and t in seconds. The wave length of the wave is …..
(a) 200 m
(b) 100 m
(c) 20 m
(d) 10 m
Answer:
(a) 200 m
![]()
Question 43.
The equation of a wave moving on string is y = 8 sin{π(0.002 x – 4t)} where x, y are in centimeter and t in seconds. The velocity of the wave is ……
(a) 100 cm/s
(b) 0.2π cm/s
(c) 4π cm/s
(d) 200 cm/s
Answer:
(d) 200 cm/s
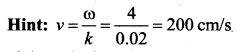
Question 44.
If the velocity of sound in air is 340 ms-1, a person singing a note of frequency 250 cps is producing sound waves with a wavelength of ……..
(a) 0.7
(b) 1.36 cm
(c) 1.36 m
(d) 85 km
Answer:
(c) 1.36
![]()
Question 45.
Asa transverse wave strikes against a fixed end …….
(a) its phase changes by 180°, but velocity does not change.
(b) its phase does not change, but velocity changes
(c) its velocity changes and phase too changes by 180°
(d) nothing can be predicted about changes in its velocity and phase.
Answer:
(a) its phase changes by 180°, but velocity does not change
Question 46.
A source of sounds is travelling with a velocity of 40 km/hr towards an observer and emits sound of frequency 2000 Hz. If the velocity of sound is 1220 km/hr, then what is the apparent frequency heard by the observer?
(a) 2068 Hz
(b) 2180 Hz
(c) 2000 Hz
(d) 1980 Hz
Answer:
(a) 2068 Hz
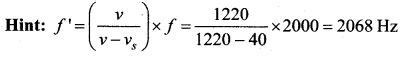
Question 47.
A vehicle with a horn of frequency n is moving with a velocity of 30m/s in a direction perpendicular to the straight line joining the observer and the vehicle. The observer perceives the sound to have a frequency n + n1. Then (if the sound velocity in air is 300 m/s)
(a) n1 = 10 n
(b) n1 = 0
(c) n1 = – 0.1 n
(d) n1 = 0.1 n
Answer:
(b) n1 = 0
Hint:
No Doppler effect is observed if the source moves perpendicular to the line joining the source and the observer. Therefore, the correct choice is (b).
Question 48.
The Doppler effect is applicable for ……..
(a) light waves
(b) sound waves
(c) space waves
(d) both (a) and (b)
Answer:
(d) both (a) and (b)
Question 49.
The speed of a wave in a medium is 760 m/s. If 3600 waves are passing through a point in the medium in 2 minutes, then its wavelength is ……
(a) 13.8 m
(b) 25.3 m
(c) 41.5 m
(d) 57.2 m
Answer:
(b) 25.3 m
![]()
Question 50.
If a sound wave travels from air to water, the quantity that remain unchanged is …….
(a) velocity
(b) wavelength
(c) frequency
(d) amplitude
Answer:
(c) frequency
Question 51.
Asa spherical wave propagates, …….
(a) the wave intensity remains constant
(b) the wave intensity decrease as the inverse of the distance from the source
(c) the wave intensity decreases as the inverse square of the distance from the source.
(d) The wave intensity decreases as the inverse cube of the distance from the source.
Answer:
(c) The wave intensity decreases as the inverse square of the distance from the source.
Question 52.
A source of sound and a listener are approaching each other with a speed of 40ms-1.The apparent frequency of a note produced by the source is 400 Hz. Then its true frequency is (velocity of sound in air = 360 ms-1)
(a) 320 Hz
(b) 400 Hz
(c) 360 Hz
(d) 420 Hz
Answer:
(a) 320 Hz
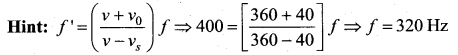
Question 53.
Sound waves of wavelength greater than that of audible sound are called ……
(a) infrasonic waves
(b) ultrasonic waves
(c) sonic waves
(d) seismic waves
Answer:
(a) infrasonic waves
Question 54.
The frequency of a sound wave is/and its velocity is v. If the frequency is increased to 4 f the velocity of the wave will be:
(a) v
(b) 2v
(c) 4 v
(d) v/4
Answer:
(a) v
Hint:
The velocity is a characteristic of the medium and, therefore, it remains constant.
Question 55.
Which of the following statement is untrue? The velocity of sound in a gas …….
(a) is independent of pressure
(b) increases with increase in temperature
(c) is dependent on molecular weight
(d) is greater in dry air than in moist air
Answer:
(d) is greater in dry air than in moist air
Question 56.
When a stone is dropped on the surface of still water, the waves produced are …….
(a) transverse
(b) longitudinal
(c) Stationary
(d) partly longitudinal and partly transverse.
Answer:
(d) Partly longitudinal and partly transverse.
Question 57.
The equation of a wave is y = 0.1 sin (100πt – kx) where x, y are in metres and t in seconds. If – the velocity of the wave is 100 m/s, then the value of k is
(a) 1 m-1
(b) 2m-1
(c) πm-1
(d) 2πm-1
Answer:
(c) πm-1
Question 58.
A transverse wave propagating on a stretched string of linear density 3 × 10-4 kg m-1 is represented by the equation, y = 0.2 sin (1.5x + 60t)
Where x is in metres and t is in seconds. The tension in the string (in newtons) is:
(a) 0.24
(b) 0.48
(c) 1.20
(d) 1.80
Answer:
(a) 0.48
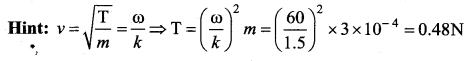
Question 59.
A transverse wave propagating along x-axis is represented by
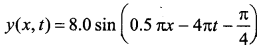
where x is in metres and t is in seconds. The speed of the wave is ……….
![]()
Answer:
(c) 8m/s
Hint:
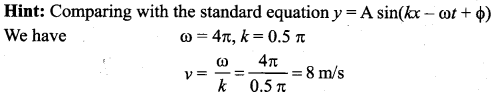
Question 60.
Two waves represented by the following equation are travelling in the same medium: y1 = 5 sin 2π (75t – 0.25 x) and y2 = 10 sin 2π (150 – 0.25x) The intensity ratio of the two waves is ……..
(a) 1 : 2
(b) 1 : 4
(c) 1 : 8
(d) 1 : 16
Answer:
(b) 1 : 4
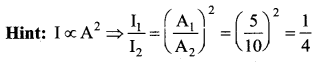
Question 61.
A point source emits sound equally in all direction is a non-absorbing medium. Two points P and Q are at distances of 2m and 3m, respectively, from the source. The ratio of the intensities of the waves at P and Q is …….
(a) 3 : 2
(b) 4 : 9
(c) 2 : 3
(d) 9 : 4
Answer:
(d) 9 : 4
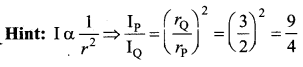
Question 62.
The waves produced by a motor boat sailing in water are ……..
(a) transverse
(b) longitudinal
(c) longitudinal and transverse
(d) stationary
Answer:
(c) longitudinal and transverse
Question 63.
Doppler effect in sound is due to ………
(a) motion of source
(b) motion of observer
(c) relative motion of source and observer
(d) none of the above
Answer:
(c) relative motion of source and observer
Question 64.
The velocity of sound in air at NTP is 330m/s. What will be its value when temperature is doubled and pressure is halved?
(a) 165 m/s
(b) 330 m/s
(c) 330 /\(\sqrt{2}\)
(d) 300/\(\sqrt{2}\) m/s
Answer:
(c) 330 /\(\sqrt{2}\)
Hint:
There is no effect of change of pressure on the velocity of sound in air. Further, v ∝ \(\sqrt{\mathrm{T}}\)
Question 65.
Sound waves travel at 350 m/s through warm air and at 3500 m/s through brass. The wavelength of a 700 Hz acoustic wave as it enters brass from warm air
(a) increases by a factor 20
(b) increases by a factor 10
(c) decreases by a factor 20
(d) decreases by a factor 10
Answer:
(b) increase by a factor 10
Hint:
Since the frequency remains the same, we have
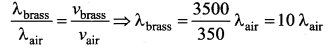
Question 66.
A train moving at a speed of 220 m/s towards a stationary object, emits a sound of frequency 1000 Hz. Some of the sound reaching the object gets reflected back to the train as echo. The frequency of the echo as detected by the driver of the train is
(a) 3000 Hz
(b) 3500 Hz
(c) 4000 Hz
(d) 5000 Hz
Answer:
(d) 5000 Hz
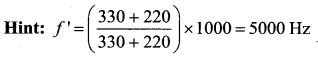
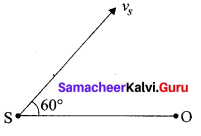
Question 67.
A source of sounds emitting waves of frequency 100 Hz and an observer O are located at same distance from each other The source is moving with a speed of 19.4 ms-1 at an angle of 60° with the source-observer line as shown in the figure. The observer is at rest. The apparent frequency observed by the observer (velocity of sound in air 330 ms-1) is ……
(a) 97 Hz
(b) 100 Hz
(c) 103 Hz
(d) 106 Hz
Answer:
(c) 103 Hz
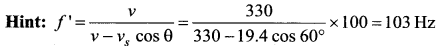
Question 68.
Beats occur because of
(a) interference
(b) reflection
(c) refraction
(d) Doppler effect
Answer:
(a) interference
Question 69.
A vibrating stretched string resonates with a tuning fork of frequency 512 Hz when the length of the string is 0.5 m. The length of the string required to vibrate resonantly with a tuning fork of frequency 256 Hz would be ……
(a) 0.25 m
(b) 0.75 m
(c) 1.0 m
(d) 2.0 m
Answer:
(c) 1.0 m
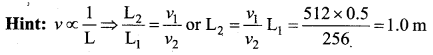
Question 70.
A cylindrical tube, open at both ends has a fundamental frequency f in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now …….
(a) f/2
(b) f
(c) 3f/4
(d) 2f
Answer:
(a) f
Hint:
When the tube is dipped in water, it become a closed pipe of length L/2. Its fundamental frequency is
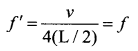
Question 71.
With the increase in temperature, the frequency of the found from an organ pipe
(a) decrease
(b) increase
(c) remains unchanged
(d) changes erractically
Answer:
(b) increase
Hint:
Frequency ∝ v/L. Now v and L both increase with temperature but increase of v is much more than the increase of L which is negligible. Thus frequency increases with temperature.
Question 72.
Two waves of the same frequency and amplitude super impose to produce a resultant disturbance of the same amplitude. The phase difference between the waves is ……
(a) zero
(b) π/3
(c) π/4
(d) 2π/3
Answer:
(d) 2π/3
Hint:
Let the amplitude of each wave be A and phase difference between them be φ. Then,
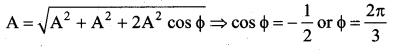
Question 73.
A sonometer wire is vibrating in the second overtone. In the wire there are ……
(a) two nodes and two antinodes
(b) one node and two antinodes
(c) four nodes and three antinodes
(d) three nodes and three antinodes
Answer:
(c) four nodes and three antinodes
Question 74.
If a resonance tube is sounded with a tuning fork of frequency 256 Hz, resonance occurs at 35 cm and 105 cm. The velocity of sound is about ……
(a) 358 m/s
(b) 512 m/s
(c) 524 m/s
(d) none of these
Answer:
(a) 358 m/s
Hint:
![]()
Question 75.
A wave of frequency 100 Hz is sent along a string towards a fixed end when this wave travels back after reflection, a node is formed at a distance of 10 cm from the fixed end of the string. The speed of the incident wave is ……
(a) 40 m/s
(b) 20 m/s
(c) 10 m/s
(d) 5 m/s
Answer:
(b) 20 m/s
Hint:
The fixed end is also a node distance between two nodes = \(\frac{\lambda}{2}\) = 10 cm
or λ = 20 cm = 0.2 cm
Speed v = fλ = 100 × 0.2 = 20 m/s
Question 76.
A standing wave is represented by y = A sin (100t) cos (0.01x) where y and A are in millimetres, t in seconds and x in metres. The velocity of the wave is ………
(a) 104 m/s
(b) 1 m/s
(c) 10-4 m/s
(d) not derivable from the above information
Answer:
(a) 104 m/s
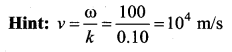
Question 77.
Two waves of the same frequency and intensity superimpose with each other in opposite phases. Then after superposition the ……
(a) intensity increases to four times
(b) intensity increase to two times
(c) frequency increases to four times
(d) none of the above
Answer:
(d) none of the above
Hint:
Since the waves are in opposite phases, the resultant intensity will be zero. The frequency remains the same. So, the correct choice is (d).
Question 78.
Two open organ pipes of lengths 50 cm and 50.5 cm produce 3 beats/s. Then the velocity of sound is …….
(a) 300 m/s
(b) 30 m/s
(c) 303 m/s
(d) 30.3 m/s
Answer:
(c) 303 m/s
![]()
Question 79.
If the ratio of the amplitudes of two waves is 4 : 3, then the ratio of maximum and minimum intensities is …….
(a) 16 : 9
(b) 49 : 16
(c) 7 : 1
(d) 49 :1
Answer:
(d) 49 : 1
Question 80.
An air column in a pipe, which is closed at one end, will be in resonance with a vibrating tuning fork of frequency 256 Hz, if the length of the column in centimeter is (velocity of sound in air = 340 m/s)
(a) 21.25
(b) 125
(c) 62.50
(d) 33.2
Answer:
(d) 33.2
Hint:
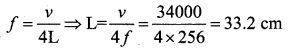
Question 81.
Two sound waves with wavelengths 5.0 cm and 5.5 cm, respectively each propagate in a gas with velocity 330 m/s. The number of beats per second will be ……..
(a) 0
(b) 1
(c) 6
(d) 12
Answer:
(c) 6
Hint:
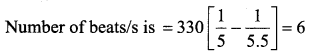
Question 82.
Two vibrating tuning forks produce progressive waves given be y1 =4 sin 500 πt and y2 = 2 sin 506 πt where t is in seconds number of beats produced per minute is ……..
(a) 60
(b) 3
(c) 369
(d) 180
Answer:
(d) 180
![]()
Question 83.
The ratio of intensities of two waves is 16 : 9. If they produce interference, then the ratio of maximum and minium intensities will be ……..
(a) 4 : 3
(b) 49 : 1
(c) 64 : 27
(d) 81 : 49
Answer:
(b) 49 : 1
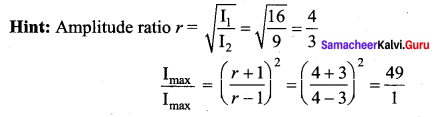
Question 84.
A closes organ pipe of length 20 cm is sounded with a tuning fork in resonance. What is the frequency of the tuning fork? (v = 332 m/s)
(a) 300 Hz
(b) 350 Hz
(c) 375 Hz
(d) 415 Hz
Answer:
(d) 415 Hz So,
Hint: In resonance, the frequency of the fork is equal to the frequency of the organ pipe,
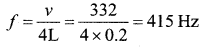
Question 85.
In a resonance tube, the first resonance is obtained at 40 cm length, using a tuning fork of frequency 450 Hz. Ignoring end correction, the velocity of sound in air is
(a) 620 m/s
(b) 720 m/s
(c) 820 m/s
(d) 1020 m/s
Answer:
(b) 720 m/s
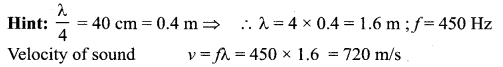
Question 86.
If we study the vibration of a pipe open at both ends, then which of the following statement is not true?
(a) open end will be antinode
(b) odd harmonics of the fundamental frequency will be generated
(c) all harmonics of the fundamental
(d) pressure change will be maximum at both ends.
Answer:
(d) pressure change will be maximum at both ends.
Hint:
Pressure change at open ends is zero.
Question 87.
The fundamental frequency of a closes organ pipe of length 20 cm is equal to the second overtone of an organ pipe open at both the ends. The length of the organ pipe open at both the ends is ……
(a) 80 cm
(b) 100 cm
(c) 120 cm
(d) 140 cm
Answer:
(c) 120 cm
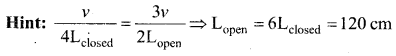
Samacheer Kalvi 11th Physics Waves 2 Mark Questions
Question 1.
Define the term wave motion?
Answer:
Wave motion is a kind of disturbances which travels through a medium due to repeated vibrations of the particles of the medium about their mean positions, the disturbance being handed over from one particle to the next.
Question 2.
What is a progressive wave?
Answer:
A wave that travels from one point of the medium to another is called a progressive wave.
Question 3.
What is a plane progressive harmonic wave?
Answer:
If during the propagation of a wave through a medium the particles of the medium vibrate simple harmonically about their mean positions, than the wave is said to be plane progressive harmonic wave.
Question 4.
What do you mean by phase of a wave?
Answer:
The phase of a harmonic is a quantity that gives complete information of the wave at any time and at any position.
Question 5.
Define wave velocity or phase velocity?
Answer:
The distance covered by a wave in the direction of its propagation per unit time is called the wave velocity.
Question 6.
What are stationary waves?
Answer:
When two identical waves of same amplitude and frequency travelling in opposite directionals with the same speed along the same path superpose each other, the resultant wave does not travel in the either direction and is called stationary or standing waves.
Question 7.
What is meant by threshold of heating?
Answer:
The lowest intensity of sound that can be perceived by the human ear is called threshold of hearing. For a sound of frequency 10 kHz, the threshold of hearing is 10-12 Wm-2
Question 8.
What is meant by reverberation?
Answer:
The persistence of audible sound after the source has ceased to emit sound is called reverberation.
Question 9.
What is musical scale?
Answer:
A series of notes whose fundamental frequencies have definite ratios and which produce a pleasing effect on the ear when sounded in succession constitute a musical scale.
Question 10.
Define reverberation time?
Answer:
It is defined as the time which sound takes to fall in intensity to one millionth (10-6) part of its original intensity after it was stopped.
Samacheer Kalvi 11th Physics Waves Numerical Problems
Question 1.
The fundamental frequency in an open organ pipe is equal to the 3rd harmonic of a closed organ pipe. If the length of the closed organ pipe is 20 cm. What is the length of the open organ pipe.
Answer:

Question 2.
Two cars moving in opposite directions approach each other with speed of 22 ms-1 and 16.5 ms-1 respectively. The driver of the first car blows a horn having a frequency 400 Hz. To find the frequency heard by the driver of the second car.
Answer:
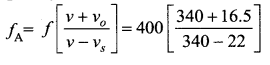
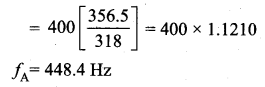
Question 3.
The second overtone of an open organ pipe has the same frequency as the 1st overtone of a closed pipe L metre long. Then what will be the length of the open pipe.
Answer:

The Length of the open pipe is two times of the length of the closed pipe.
Question 4.
A steel wire 0.72 m long has a mass of 5.0 × 10-3 kg. If the wire is under a tension of 60 N. What is the speed of transverse waves on the wire?
Answer:

Question 5.
Estimate the speed of sound ¡n air at standard temperature and pressure by using
(i) Newton’s formula and
(ii) Laplace formula. The mass of 1 moIe of air = 29. 0 × 10-3 kg. For air, γ = 1.4
Answer:
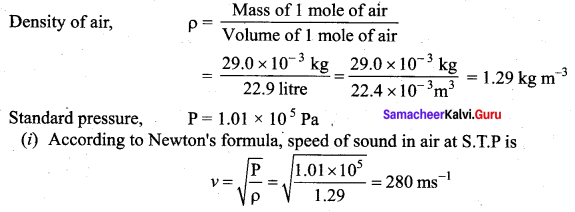
(ii) According to Newton’s formula speedof sound in air at S.T.P is
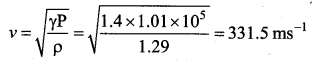
Question 6.
An observer moves towards a stationary source of sound with a velocity one-fifth of the velocity of sound. What Is the percentage increase in the apparent frequency?
Answer:
Here observer moves towards the stationary source.
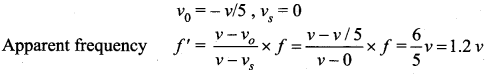
The percentage increase in apparent frequency
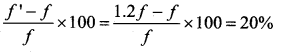
Question 7.
Tube A has both ends open, while B has on end closed otherwise the two tubes are identical. What Is the ratio of fundamental frequency of the tubes A and B?
Answer:
The fundamental frequency for tube A with both ends open is fA = \(\frac{v}{2 \mathrm{L}}\)
The fundamental frequency for tube B with one end closed is fB = \(\frac{v}{4 \mathrm{L}}\)
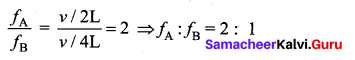
Question 8.
A train moves towards a stationary observer with speed 34 mIs. The train sounds a whistle and its frequency registered by the observer is f1. If the train’s speed is reduced to 17 m/s, the frequency registered f2. If the speed of sound is 340 m/s, then find the ratio f1/f2
Answer:
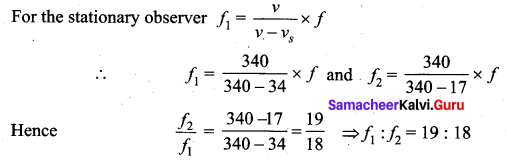
Question 9.
A police car with a siren of frequency 8 kHz ¡s moving with uniform velocity 36 km/h towards a tall building which reflect the sound waves. The speed of sound In air is 320m/s. What is the frequency of the siren heard by the car driver?
Answer:
(a) Frequency received by the building.
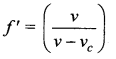
The wall (source) reflect this frequency, So frequency heard by the car driver is
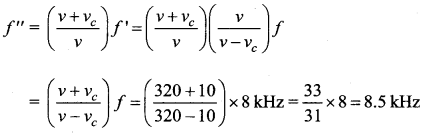
Question 10.
The displacement y of a wave travelling in the x-direction ¡s given by y = 10-4 sin (600t – 2x + π/3)
Where x is expressed in metres and t is seconds. What is the speed of the wave motion (in ms-1)?
Answer:
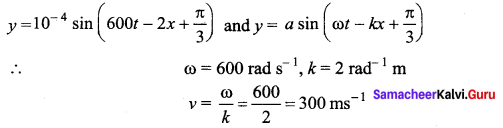
We believe the information shared regarding Samacheer Kalvi Class 11th Physics Solutions Chapter 11 Waves Questions and Answers as far as our knowledge is concerned is true and reliable. In case of any queries or suggestions do leave us your feedback and our team will guide you at the soonest possibility. Bookmark our site to avail latest updates on several Tamilnadu State Board Solutions at your fingertips.