Students can download 12th Business Maths Chapter 2 Integral Calculus I Ex 2.6 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.6
Integrate the following with respect to x.
Question 1.
\(\frac{2 x+5}{x^{2}+5 x-7}\)
Solution:

Question 2.
\(\frac{e^{3 \log x}}{x^{4}+1}\)
Solution:
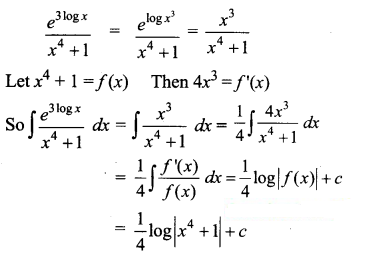
Question 3.
\(\frac{e^{2 x}}{e^{2 x}-2}\)
Solution:

Question 4.
\(\frac{(\log x)^{3}}{x}\)
Solution:

Question 5.
\(\frac{6 x+7}{\sqrt{3 x^{2}+7 x-1}}\)
Solution:

Question 6.
\((4 x+2) \sqrt{x^{2}+x+1}\)
Solution:
\((4 x+2) \sqrt{x^{2}+x+1}\)
Let f(x) = x2 + x + 1
then f'(x) = 2x + 1

Question 7.
x8 (1 + x9)5
Solution:

Question 8.
\(\frac{x^{e-1}+e^{x-1}}{x^{e}+e^{x}}\)
Solution:

Question 9.
\(\frac{1}{x \log x}\)
Solution:

Question 10.
\(\frac{x}{2 x^{4}-3 x^{2}-2}\)
Solution:

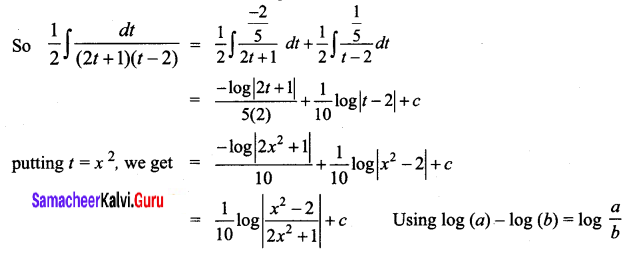
Question 11.
ex (1 + x) log(x ex)
Solution:
ex (1 + x) log(x ex) = (ex + x ex) log (x ex)
Let z = x ex, Then dz = d(x ex)
dz = (x ex + ex) dx (Using product rule)
So ∫ ex (1 + x) log (x ex) dx
= ∫ log (x ex) (ex + x ex) dx
= ∫ log z dz
= z (log z – 1) + c
= x ex [log (x ex) – 1] + c
Question 12.
\(\frac{1}{x^{2}\left(x^{2}+1\right)}\)
Solution:

Question 13.
\(e^{x}\left[\frac{1}{x^{2}}-\frac{2}{x^{3}}\right]\)
Solution:
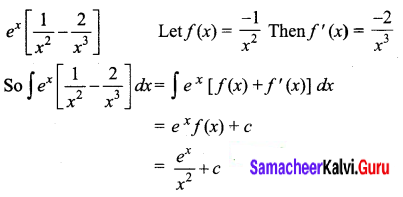
Question 14.
\(e^{x}\left[\frac{x-1}{(x+1)^{3}}\right]\)
Solution:
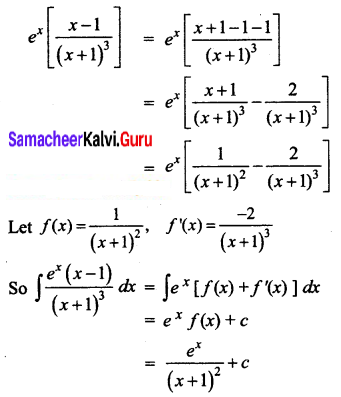
Question 15.
\(e^{3 x}\left[\frac{3 x-1}{9 x^{2}}\right]\)
Solution:
