Students can download 12th Business Maths Chapter 3 Integral Calculus II Ex 3.3 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.3
Question 1.
Calculate consumer’s surplus if the demand function p = 50 – 2x and x = 20
Solution:
Given demand function p = 50 – 2x, x0 = 20

Hence the consumer’s surplus is 400 units.
Question 2.
Calculate consumer’s surplus if the demand function p = 122 – 5x – 2x2, and x = 6
Solution:
Demand function p = 122 – 5x – 2x2 and x = 6
when x = x0 = 6
p0 = 122 – 5(6) – 2(36)
= 122 – 30 – 72
= 20

Hence the consumer’s surplus is 378 units
Question 3.
The demand function p = 85 – 5x and supply function p = 3x – 35. Calculate the equilibrium price and quantity demanded. Also, calculate consumer’s surplus.
Solution:
Given pd = 85 – 5x and ps = 3x – 35
At equilibrium prices pd = ps
85 – 5x = 3x – 35
⇒ 8x = 120
⇒ x = 15
p0 = 85 – 5(15) = 85 – 75 = 10

The equilibrium price is ₹10, the quantity demanded is 15. The consumer surplus is 562.50 units.
Question 4.
The demand function for a commodity is p = e-x .Find the consumer’s surplus when p = 0.5.
Solution:
Given demand function p = e-x
At p = 0.5, (i.e) p0 = 0.5,
we have p0 = \(e^{-x_{0}}\)
⇒ 0.5 = \(e^{-x_{0}}\)
Taking loge on both sides
loge(0.5) = -x0

Question 5.
Calculate the producer’s surplus at x = 5 for the supply function p = 7 + x.
Solution:
Given supply function is p = 7 + x, x0 = 5
p0 = 7 + x0 = 7 + 5 = 12
Producer’s surplus
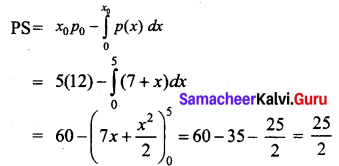
Hence the producer’s surplus is \(\frac{25}{2}\) units
Question 6.
If the supply function for a product is p = 3x + 5x2. Find the producer’s surplus when x = 4.
Solution:
Given the supply function ps = 3x + 5x2
when x = 4, (i.e) x0 = 4,
p0 = 3 (4) + 5(4)2 = 12 + 80 = 92
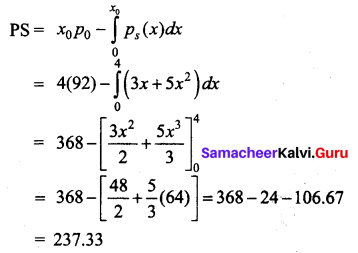
Hence the producer’s surplus is 237.3 units.
Question 7.
The demand function for a commodity is p = \(\frac{36}{x+4}\). Find the consumer’s surplus when the prevailing market price is ₹ 6.
Solution:
Given p = \(\frac{36}{x+4}\)
The marker price is ₹6 (i.e) p0 = 6

So the consumer’s surplus when the prevailing market price is ₹ 6 is (36 log \(\frac{3}{2}\) – 12) units.
Question 8.
The demand and supply functions under perfect competition are pd = 1600 – x2 and ps = 2x2 + 400 respectively. Find the producer’s surplus.
Solution:
Given demand function pd = 1600 – x2 and
Supply function ps = 2x2 + 400
Perfect competition means there is equilibrium between supply and demand
ps = pd
⇒ 1600 – x2 = 2x2 + 400
⇒ 3x2 = 1200
⇒ x2 = 400
⇒ x = ± 20
The value of x cannot be negative. So x = 20 we take x0 = 20.
p0 = 1600 – (20)2 = 1600 – 400 = 1200
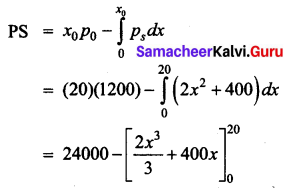
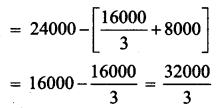
Hence the producer’s surplus is \(\frac{32000}{3}\) units.
Question 9.
Under perfect competition for a commodity the demand and supply laws are \(p_{d}=\frac{8}{x+1}-2\) and \(p_{s}=\frac{x+3}{2}\) respectively. Find the consumer’s and producer’s surplus.
Solution:
Given \(p_{d}=\frac{8}{x+1}-2\) and \(p_{s}=\frac{x+3}{2}\)
Here, since there is perfect competition, there is equilibrium, that is pd = ps
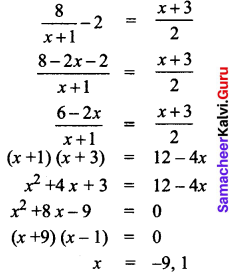
Since the value of x cannot be negative, x = 1 we take this value as x0

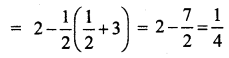
Hence under perfect competition,
(i) The consumer’s surplus is (8 log 2-4) units
(ii) The producer’s surplus is \(\frac{1}{4}\) units.
Question 10.
The demand equation for a products is x = \(\sqrt{100-p}\) and the supply equation is x = \(\frac{p}{2}\) – 10. Determine the consumer’s surplus and producer’s surplus, under market equilibrium.
Solution:
Given demand equation is x = \(\sqrt{100-p}\) and supply equation is x = \(\frac{p}{2}\) – 10
So the demand law is x2 = 100 – p
⇒ pd = 100 – x2
Supply law is given by x + 10 = \(\frac{p}{2}\)
⇒ ps = 2(x + 10)
Under equilibrium pd = ps
⇒ 100 – x2 = 2(x + 10)
⇒ 100 – x2 = 2x + 20
⇒ x2 + 2x – 80 = 0
⇒ (x + 10) (x – 8) = 0
⇒ x = -10, 8
The value of x cannot be negative, So x = 8
When x0 = 8, p0 = 100 – 82 = 100 – 64 = 36
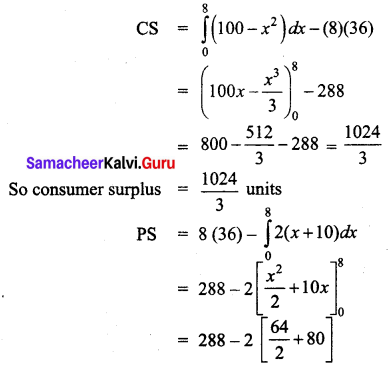
= 288 – 2(112)
= 64
So the producer’s surplus is 64 units.
Question 11.
Find the consumer’s surplus and producer’s surplus for the demand function pd = 25 – 3x and supply function ps = 5 + 2x.
Solution:
Given pd = 25 – 3x and ps = 5 + 2x
At market equilibrium, pd = pss
⇒ 25 – 3x = 5 + 2x
⇒ 5x = 20
⇒ x = 4
When x0 = 4, p0 = 25 – 12 = 13
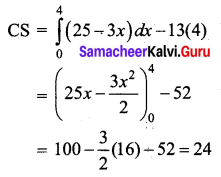
So the consumer’s surplus is 24 units.
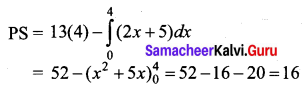
So the producer’s surplus is 16 units.