Students can download 12th Business Maths Chapter 3 Integral Calculus II Miscellaneous Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Miscellaneous Problems
Question 1.
A manufacture’s marginal revenue function is given by MR = 275 – x – 0.3x2. Find the increase in the manufactures total revenue if the production is increased from 10 to 20 units.
Solution:
Given MR = 275 – x – 0.3x2
R = ∫(MR) dx + k
But given that production is increased from 10 to 20 units. so,

Thus the total revenue is increased by ₹ 1900
Question 2.
A company has determined that marginal cost function for x product of a particular commodity is given by MC = 125 + 10x – \(\frac{x^{2}}{9}\). Where C is the cost of producing x units of the commodity. If the fixed cost is ₹ 250 what is the cost of producing 15 units.
Solution:

Question 3.
The marginal revenue function for a firm is given by MR = \(\frac{2}{x+3}-\frac{2 x}{(x+3)^{2}}+5\). Show that the demand function is P = \(\frac{2}{x+3}\) + 5
Solution:


Question 4.
For the marginal revenue function MR = 6 – 3x2 – x3, Find the revenue function and demand function.
Solution:
MR = 6 – 3x2 – x3
Revenue function R = ∫(6 – 3x2 – x3) dx + k

Question 5.
The marginal cost of production of a firm is given by C'(x) = 20 + \(\frac{x}{20}\) the marginal revenue is given by R'(x) = 30 and the fixed cost is ₹ 100. Find the profit function.
Solution:

Question 6.
The demand equation for a product is pd = 20 – 5x and the supply equation is ps = 4x + 8. Determine the consumer’s surplus and producer’s surplus under market equilibrium.
Solution:
Given pd = 20 – 5x and ps = 4x + 8
Under market equilibrium, pd = ps
20 – 5x = 4x + 8

Consumer’s surplus,

Producers surplus,

Hence at market equilibrium,
(i) the consumer’s surplus is \(\frac{40}{9}\) units
(ii) the producer’s surplus is \(\frac{32}{9}\) units
Question 7.
A company requires f(x) number of hours to produce 500 units. It is represented by f(x) = 1800x-0.4. Find out the number of hours required to produce additional 400 units. [(900)0.6 = 59.22, (500)0.6 = 41.63]
Solution:
Given that for producing 500 units, the company requires f(x) = 1800 x-0.4 hours.
Now it has to produce an additional 400 units.
So totally 900 units.
No. of hours needed

Question 8.
The price elasticity of demand for a commodity is \(\frac{p}{x^{3}}\). Find the demand function if the quantity of demand is 3 when the price is ₹ 2.
Solution:

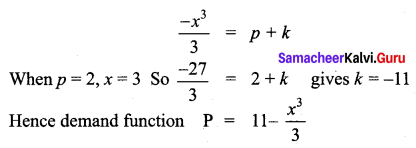
Question 9.
Find the area of the region bounded by the curve between the parabola y = 8x2 – 4x + 6 the y-axis and the ordinate at x = 2.
Solution:
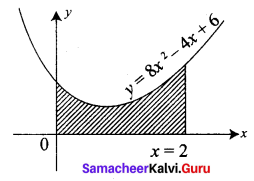
The shaded region is the area required.

Question 10.
Find the area of the region bounded by the curve y2 = 27x3 and the lines x = 0, y = 1 and y = 2.
Solution:
The given curve is y2 = 27x3
The lines are x = 0, y = 1 and y = 2
