Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Additional Problems

Students can download 12th Business Maths Chapter 4 Differential Equations Additional Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Additional Problems

I. One Mark Questions

Choose the correct answer.

Question 1.
The differential equation of straight lines passing through the origin is ______
(a) \(\frac{x d y}{d x}=y\)
(b) \(\frac{d y}{d x}=\frac{x}{y}\)
(c) \(\frac{d y}{d x}=0\)
(d) \(\frac{x d y}{d x}=\frac{1}{y}\)
Answer:
(a) \(\frac{x d y}{d x}=y\)
Hint:

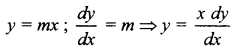
Question 2.
The solution of x dy + y dx = 0 is _______
(a) x + y = c
(b) x² + y² = c
(c) xy = c
(d) y = cx
Answer:
(c) xy = c
Hint:
x dy + y dx = 0
d(xy) = 0
xy = c

Question 3.
The solution of x dx + y dy = 0 is _____
(a) x² + y² = c
(b) \(\frac{x}{y}\) = c
(c) x² – y² = c
(d) xy = c
Answer:
(a) x² + y² = c
Hint:
x dx = -y dy
\(\frac{x^{2}}{2}=\frac{-y^{2}}{2}+c_{1}\)
x² + y² = c

Question 4.
The solution of \(\frac{d y}{d x}\) = e^x-y is ______
(a) e^y e^x = c
(b) y = log ce^x
(c) y = log(e^x + c)
(d) e^x+y = c
Answer:
(c) y = log(e^x + c)
Hint:

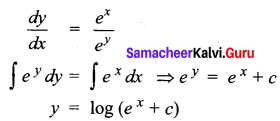
Question 5.
The solution of \(\frac{d p}{d t}\) = ke^-t (k is a constant) is ________
(a) \(c-\frac{k}{e^{t}}=p\)
(b) p = ke^t + c
(c) t = log\(\frac{c-p}{k}\)
(d) t = log_c p
Answer:
(a) \(c-\frac{k}{e^{t}}=p\)
Hint:

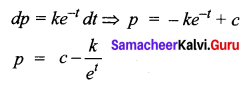
Question 6.
The integrating factor of (1 + x²) \(\frac{d y}{d x}\) + xy = (1 + x²)³ is _______
(a) \(\sqrt{1+x^{2}}\)
(b) log(1 + x²)
(c) \(e^{\tan ^{-1} x}\)
(d) \(\log ^{\left(\tan ^{-1} x\right)}\)
Answer:
(a) \(\sqrt{1+x^{2}}\)
Hint:

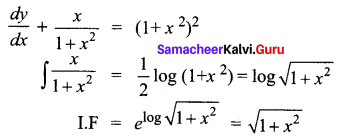
Question 7.
The complementary function of the differential equation (D² – D) y = e^x is _____
(a) A + B e^x
(b) (Ax + B) e^x
(c) A + B e^-x
(d) (A + Bx) e^-x
Answer:
(a) A + B e^x
Hint:
m² – m = 0
m(m – 1) = 0
CF = Ae^0x + Be^x = A + B e^x

Question 8.
Match the following
(a) \(\frac{d^{4} y}{d x^{4}}\) + sin y = 0 – (i) order 1, degree 1
(b) y’ + y = e^x – (ii) order 3, degree 2
(c) y'” + 2y” + y’ = 0 – (iii) order 4, degree 1
(d) (y”’)² + y’ + y⁵ = 0 – (iv) order 3, degree 1
Answer:
(a) – (iii)
(b) – (i)
(c) – (iv)
(d) – (ii)

Question 9.
Fill in the blanks
(a) The general solution of the equation \(\frac{d y}{d x}+\frac{y}{x}=1\) is ______
(b) Integrating factor of \(\frac{x d y}{d x}\) – y = sin x is ______
(c) The differential equation of y = A sin x + B cos x is _______
(d) The D.E \(\frac{d y}{d x}+\frac{y}{x \log x}=\frac{1}{x}\) is a ________ differential equation.
Answer:
(a) \(y=\frac{x}{2}+\frac{c}{x}\)
(b) \(\frac{1}{x}\)
(c) \(\frac{d^{2} y}{d x^{2}}+y=0\)
(d) linear

Question 10.
State true or false
(a) y = 3 sin x + 4 cos x is a particular solution of the differential equation \(\frac{d^{2} y}{d x^{2}}\) + y = 0
(b) The solution of \(\frac{d y}{d x}=\frac{x+2 y}{x}\) is x + y = kx²
(c) y = 13e^x + 4e^-x is a solution of \(\frac{d^{2} y}{d x^{2}}\) – y = 0
Answer:
(a) True
(b) True
(c) True

II. 2 Marks Questions

Question 1.
Form the D.E of the family of curves y = ae^3x + be^x where a, b are parameters
Solution:
y = ae^3x + be^x
\(\frac{d y}{d x}\) = 3 ae^3x + be^x

Question 2.
Find the D.E of a family of curves y = a cos (mx + b), a and b are constants.
Solution:

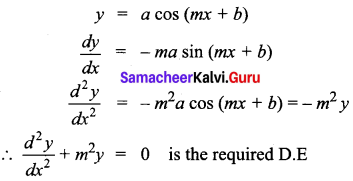
Question 3.
Find the D.E by eliminating the constants a and b from y = a tan x + b sec x
Solution:

Question 4.
Solve: \(\frac{d y}{d x}=e^{7 x+y}\)
Solution:

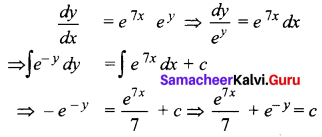
Question 5.
Solve: (x² – ay) dx = (ax – y²) dy
Solution:
Writing the equation as
x² dx + y² dy = a (x dy + y dx)
x² dx + y² dy = a d(xy)
∫x² dx + ∫y² dy = a ∫d(xy) + c
\(\frac{x^{3}}{3}+\frac{y^{3}}{3}\) = axy + c
Hence the general solution is x³ + y³ = 3axy + c

Question 6.
Solve (sin x + cos x) dy + (cos x – sin x) dx = 0
Solution:
The given equation can be written as

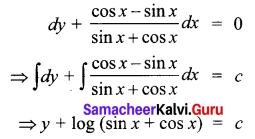
III. 3 and 5 Marks Questions

Question 1.
Solve \(\frac{x d y}{d x}\) + cos y = 0, given y = \(\frac{\pi}{4}\) when x = √2
Solution:

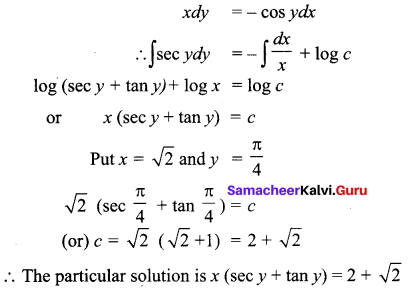
Question 2.
The slope of a curve at any point is the reciprocal of twice the ordinate of the point. The curve also passes through the point (4, 3). Find the equation of the curve.
Solution:
Slope at any point (x, y) is the slope of the tangent at (x, y)
\(\frac{d y}{d x}=\frac{1}{2 y}\)
⇒ 2y dy = dx
⇒ ∫2y dy = ∫dx + c
⇒ y² = x + c
Since the curve passes through (4, 3)
we have 9 = 4 + c ⇒ c = 5
Equation of the curve is y² = x + 5

Question 3.
The net profit P and quantity x satisfy the differential equation \(\frac{d p}{d x}=\frac{2 p^{3}-x^{3}}{3 x p^{2}}\). Find the relationship between the net profit and demand given that p = 20 when x = 10
Solution:

Question 4.
Solve: \(\frac{d y}{d x}\) + ay = e^x (a ≠ -1)
Solution:
The given equation is of the form \(\frac{d y}{d x}\) + Py = Q
Here P = a, Q = e^x
The general solution is y (I.F) = ∫Q (I.F) dx + c

Question 5.
Solve: \(\frac{d y}{d x}\) + y cos x = \(\frac{1}{2}\) sin 2x
Solution:
Here P = cos x, Q = \(\frac{1}{2}\) sin 2x

Question 6.
Solve (D² – 6D + 25) y = 0
Solution:
The auxiliary equations is m² – 6m + 25 = 0

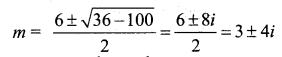
The Roots are complex and of the form,
α ± β with α = 3 and β = 4
The complementary function = e^3x (A cos 4x + B sin 4x)
The general solution is y = e^3x (A cos 4x + B sin 4x)

Question 7.
Solve (D² + 10D + 25) y = \(\frac{5}{2}\) + e^-5x
Solution:
The auxiliary equations is m² + 10m + 25 = 0
(m + 5)² = 0
m = -5, -5
The complementary function = (Ax + B) e^-5x

Question 8.
Suppose that the quantity demanded Q_d = 40 – 4p – 4\(\frac{d p}{d t}+\frac{d^{2} p}{d t^{2}}\) and quantity supplied Q_s = -6 + 8p where p is the price. Find the equilibrium price for market clearance.
Solution:
For market clearance, the required condition is Q_d = Q_s