Students can download 12th Business Maths Chapter 4 Differential Equations Ex 4.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.2
Question 1.
Solve
(i) \(\frac{d y}{d x}=a e^{y}\)
(ii) \(\frac{1+x^{2}}{1+y}=x y \frac{d y}{d x}\)
Solution:

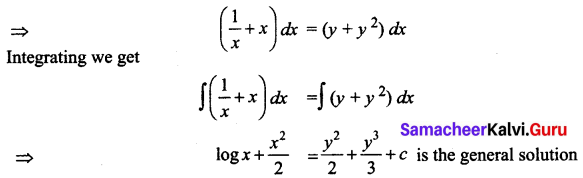
Question 2.
Solve: y(1 – x) – x \(\frac{d y}{d x}\) = 0
Solution:
y(1 – x) – x \(\frac{d y}{d x}\) = 0
Separating the variables,

log x – x = log y + c is the general solution
Question 3.
Solve:
(i) y dx – x dy = 0
(ii) \(\frac{d y}{d x}\) + ex + y ex = 0
Solution:
(i) y dx – x dy = 0
Separating the variables,
y dx = x dy

Integrating,
\(\int \frac{1}{y+1} d y=\int-e^{x} d x\)
log (y + 1) = -ex + c is the general solution
Question 4.
Solve: cos x (1 + cos y) dx + sin y (1 + sin x) dy = 0
Solution:
cos x (1 + cos y) dx + sin y (1 + sin x) dy = 0
Separating the variables,
cos x (1 + cos y) dx = -sin y (1 + sin x) dy

Question 5.
Solve: (1 – x) dy – (1 + y) dx = 0
Solution:
(1 – x) dy – (1 + y) dx = 0
Separating the variables,
(1 – x)dy = (1 + y) dx
\(\frac{d y}{1+y}=\frac{d x}{1-x}\)
Integrating, we get
\(\int \frac{1}{1+y} d y=\int \frac{1}{1-x} d x\)
log(y + 1) = -log(1 – x) + log c
log(y + 1) + log(1 – x) = log c
(y + 1) (1 – x) = c
Question 6.
Solve:
(i) \(\frac{d y}{d x}\) = y sin 2x
(ii) log(\(\frac{d y}{d x}\)) = ax + by
Solution:
(i) \(\frac{d y}{d x}\) = y sin 2x
Separating the variables, \(\frac{d y}{y}\) = sin 2x dx
Integrating, we get
∫\(\frac{1}{y}\) dy = ∫sin 2x dx
log y = \(-\frac{\cos 2 x}{2}+c\) is the required solution

Question 7.
Find the curve whose gradient at any point P(x, y) on it is \(\frac{x-a}{y-b}\) and which passes through the origin.
Solution:
The gradient at any point P (x, y) on the curve is given by \(\frac{d y}{d x}\)
According to the problem
\(\frac{d y}{d x}=\frac{x-a}{y-b}\)
Separating the variables,
(y – b) dy = (x – a) dx
Integrating,
∫(y – b) dy = ∫(x – a) dx

(or) (y – b)2 = (x – a)2 + b2 – a2 is the required equation of the curve.