Students can download 12th Business Maths Chapter 5 Numerical Methods Miscellaneous Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Miscellaneous Problems
Question 1.
If f(x) = eax then show that f(0), ∆f(0), ∆2 f(0) are in G.P
Solution:

Question 2.
Prove that
(i) (1 + ∆) (1 – ∇) = 1
(ii) ∆∇ = ∆ – ∇
(iii) E∇ = ∆ – ∇E
Solution:
(i) To show (1 + ∆) (1 – ∇) = 1


Hence proved.
![]()
Question 3.
A second degree polynomial passes through the point (1, -1) (2, -1) (3, 1) (4, 5). Find the polynomial.
Solution:
Given values can be tabulated as follows
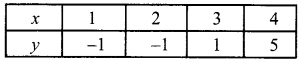
We have to find a second-degree polynomial.
We use Newton’s forward interpolation formula

The difference table is given below
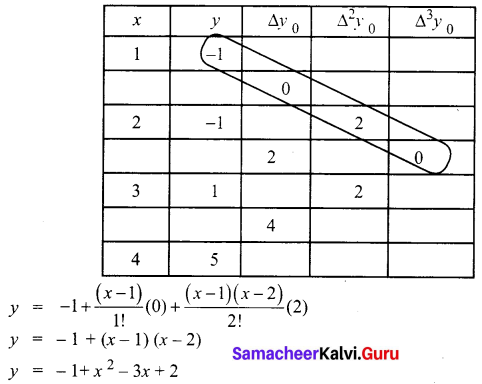
(or) y = x2 – 3x + 1 is the required second-degree polynomial which passes through the given points
Question 4.
Find the missing figures in the following table

Solution:
Since only four values of y are given, the polynomial which fits the data is of degree three.
Hence fourth differences are zero.


Thus the missing figures are 14.25 and 23.5
![]()
Question 5.
Find f(0.5) if f(-1) = 202, f(0) = 175, f(1) = 82 and f(2) = 55
Solution:
The given data can be written as

We have to find y when x = 0.5.
We use Newton’s forward interpolation formula
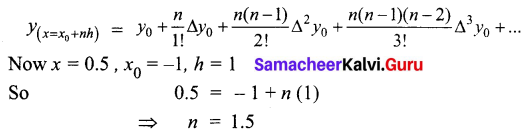
The difference table is
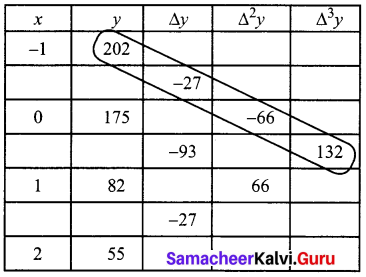
Using these values we get,

Thus the value of f(0.5) = 128.5
Question 6.
From the following data find y at x = 43 and x = 84

Solution:
We have to find the value of y at (a) x = 43 and (b) x = 84
(a) x = 43.
The value of y is required at the beginning of the table.
So we use Newton’s forward interpolation formula
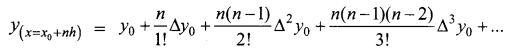
Here x = 43 , x0 = 40, h = 10
So 43 = 40 + 10n
n = 0.3
The difference table is given below
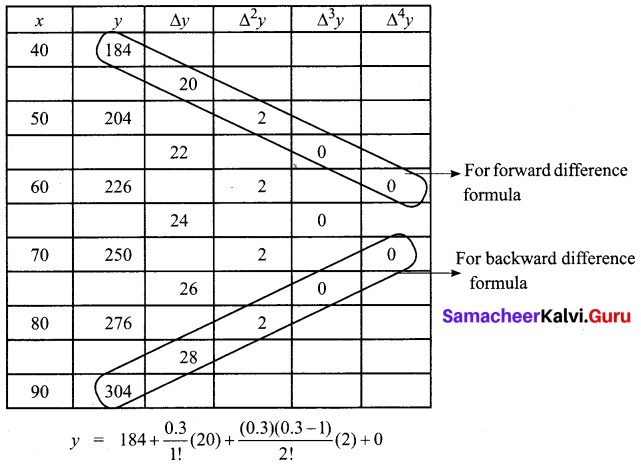
y = 184 + 6 – 0.21
y = 189.79
(b) x = 84.
The value of y is required at the end of the table.
So we use Newton’s backward interpolation formula

We use the back difference values from the table
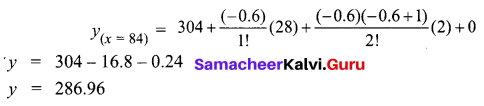
Hence the value of y at x = 43 is 189.75 and the value of y at x = 84 is 286.96
![]()
Question 7.
The area A of a circle of diameter ‘d’ is given for the following values

Find the approximate values for the areas of circles of diameter 82 and 91 respectively.
Solution:
Let diameter be x and area be y
We have to find value of y when (a) x = 82 and (b) x = 91
We first find the difference as given below
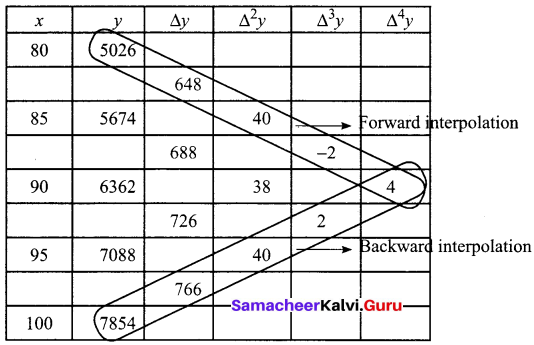


Hence the area of a circle when the diameter is 82 is 5281
area of a circle when the diameter is 91 is 6504.
Question 8.
If u0 = 560, u1 = 556, u2 = 520, u4 = 385, show that u3 = 465
Solution:
Given u0 = 560, u1 = 556, u2 = 520, u4 = 385
Since only four values are given,

![]()
Question 9.
From the following table obtain a polynomial of degree y in x

Solution:
To find a polynomial y = f(x)
Here x0 = 1, h = 1
x = x0 + nh
x = 1 + n(1)
n = x – 1
We find the forward differences as below
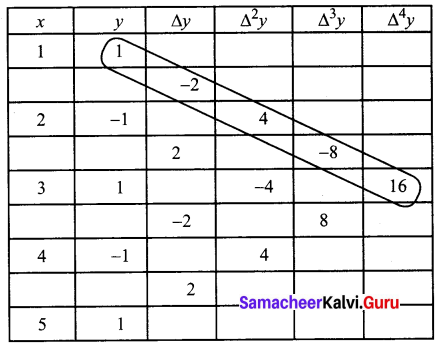
Using Newton’s forward interpolation formula,

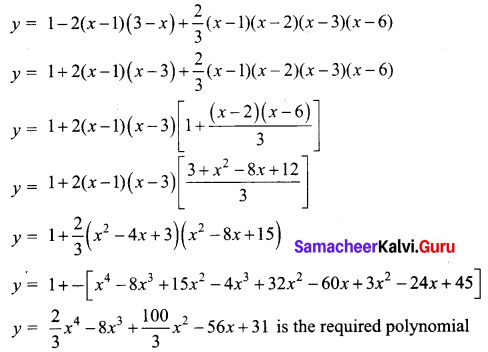
Question 10.
Using Lagrange’s interpolation formula find a polynomial which passes through the points (0, -12), (1, 0), (3, 6) and (4, 12).
Solution:
The given values are
x0 = 0, y0 = -12
x1 = 1, y1 = 0
x2 = 3, y2 = 6
x3 = 4, y3 = 12
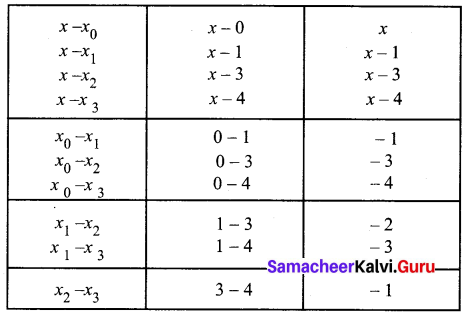
By Lagrange’s interpolaiton formula,

⇒ y = (x – 1) (x – 3) (x – 4) – x (x – 1) (x – 4) + x (x – 1) (x – 3)
⇒ y = (x – 1) (x – 4)[(x – 3) – x] + x (x – 1) (x – 3)
⇒ y = (x – 1) (x – 4) (-3) + x (x – 1) (x – 3)
⇒ y = (x – 1) [-3x + 12 + x2 – 3x]
⇒ y = (x – 1) (x2 – 6x + 12)
⇒ y = x3 – 6x2 + 12x – x2 + 6x – 12
y = x3 – 7x2 + 18x – 12 is the required polynomial which passes through the given points