Students can download 12th Business Maths Chapter 6 Random Variable and Mathematical Expectation Additional Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Additional Problems
One Mark Questions
Question 1.
If a fair coin is tossed three times the probability function p(x) of the number of heads x is _______
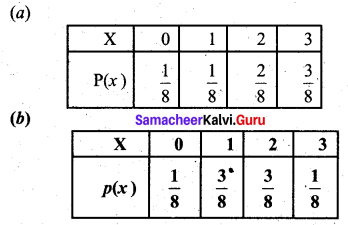
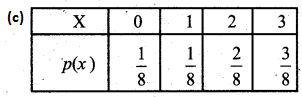
(d) None of these
Answer:
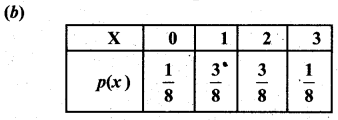
Hint:
The sample space is HHH, HHT, HTH, HTT, THH, THT, TTH and TTT
Number of heads is 0, 1, 2, 3 with probability \(\frac{1}{8}, \frac{3}{8}, \frac{3}{8}\) and \(\frac{1}{8}\)
Question 2.
If a discrete random variable has the probability mass function as
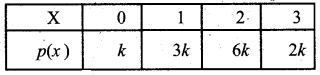
then the value of K is _______
(a) \(\frac{1}{11}\)
(b) \(\frac{1}{12}\)
(c) \(\frac{2}{13}\)
(d) \(\frac{4}{9}\)
Answer:
(b) \(\frac{1}{12}\)
Hint:
k + 3 k + 6k + 2k = 1
⇒ 12k = 1
⇒ k = \(\frac{1}{12}\)
![]()
Question 3.
If the probability density function of X is f(x) = Cx (2 – x), and 0 < x < 2, then value of C is ______
(a) \(\frac{4}{3}\)
(b) \(\frac{6}{5}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{3}{5}\)
Answer:
(c) \(\frac{3}{4}\)
Hint:

Question 4.
The random variables X and Y are independent if ______
(a) E(XY) = 1
(b) E(XY) = 0
(c) E(XY) = E(X) E(Y)
(d) E(X + Y) = E(X) + E(Y)
Answer:
(c) E(XY) = E(X) E(Y)
![]()
Question 5.
If a random variable X has the following distribution
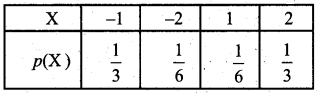
then the expected value of X is ______
(a) \(\frac{3}{2}\)
(b) \(\frac{1}{6}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{3}\)
Answer:
(b) \(\frac{1}{6}\)
Hint:
E(X) = \(\frac{-1}{3}-\frac{2}{6}+\frac{1}{6}+\frac{2}{3}=\frac{1}{3}-\frac{1}{6}=\frac{1}{6}\)
Question 6.
Var (4X + 7) = _____
(a) 7
(b) 16 Var (X)
(c) 11
(d) None of these
Answer:
(b) 16 Var (X)
Hint:
Var (4X + 7) = (42) Var (X)
![]()
Question 7.
Match the following:
| (a) Random variable | (i) Arithmetic mean |
| (b) Speed of a car | (ii) Discrete variable |
| (c) E(aX + b) | (iii) Chance variable |
| (d) No. of students in a class | (iv) Continuous variable |
| (e) E(X) | (v) aE(X) + b |
Answer:
(a) – (iii)
(b) – (iv)
(c) – (v)
(d) – (ii)
(e) – (i)
Question 8.
If E(X) = 2 and E(Z) = 4, then E (Z – X) is ______
(a) 2
(b) 6
(c) 0
(d) -2
Answer:
(a) 2
Hint:
E(Z – X) = E(Z) – E(X) = 4 – 2 = 2
![]()
Question 9.
Fill in the blanks:
- The distribution function F (X) is equal to _______
- Two types of random variables are ______ and ______
- Probability mass function is also called ______
- Cumulative distribution function is also called ________
- Probability density function is also called ______ and _______
- d F(x) is known as ______ of X.
- E(X) is denoted by _______
- Variance is a measure of ______ or _______ of X.
- Standard deviation is defined as _______
- Mean is the _______ of a density. Variance is the ________ of a density.
Answers:
- P(X ≤ x)
- discrete and continuous
- discrete probability function
- distribution function
- continuous probability function, integrating the density function
- probability differential
- µx
- the spread, dispersion of the density
- √Var[X]
- center of gravity, the moment of inertia.
2 Mark Questions
Question 1.
Verify whether the following function is a probability mass function or not. Hence find c.d.f.

Solution:
Σpi = \(\frac{1}{3}+\frac{2}{3}\) = 1 and pi > 0.
So the given function is a p.m.f. c.d.f is given by
F (x) = P (X ≤ x)
F(1) = P(X ≤ 1) = P(X = 1) = \(\frac{1}{3}\)
F(2) = P (X ≤ 2) = P(X = 1) + P (X = 2) = \(\frac{1}{3}+\frac{2}{3}\) = 1

Question 2.
Consider the following probability distribution of X.

Is p(xi) a p.m.f?
Solution:
p(xi) > 0 for all i

Hence p(xi) is a p.m.f.
![]()
Question 3.
The probability that a man fishing at a particular place will catch 1, 2, 3 and 4 fish are 0.4, 0.3, 0.2 and 0.1. What is the expected number of fish caught?
Solution:
Let X denote the no.of fish caught by the man.

E(X) = 1(0.4) + 2 (0.3) + 3 (0.2) + 4 (0.1)
= 0.4 + 0.6 + 0.6 + 0.4
= 2
Question 4.
A random variable X has the following probability function.

Find the value of K.
Solution:
We know that Σp(xi) = 1
⇒ 0.1 + K + 0.2 + 2K + 0.3 + K = 1
⇒ 4K + 0.6 = 1
⇒ 4K = 0.4
⇒ K = 0.1
![]()
Question 5.
A person receives a sum of rupees equal to the square of the number that appears on the face when a die is tossed. How much money can he expect to receive?
Solution:
Let the random variable X denote the square of the number that can appear on the face of a die. Then the distribution is given by
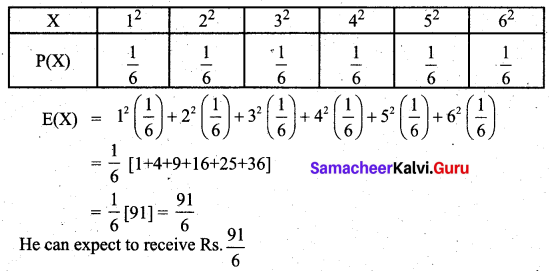
3 and 5 Marks Questions
Question 1.
For the following distribution of X.
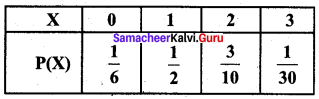
(i) P(X ≤ 1)
(ii) P(X ≤ 2 )
(iii) P(0 < X < 2)
Solution:
(i) P(X ≤ 1) = P (X = 1) + P (X = 0)
\(=\frac{1}{2}+\frac{1}{6}=\frac{4}{6}=\frac{2}{3}\)
(ii) P(X ≤ 2) = P(X = 2) + P(X = 1) + P(X = 0)
\(=\frac{3}{10}+\frac{1}{2}+\frac{1}{6}=\frac{29}{30}\)
(iii) P(0 < X < 2) = P(X = 1) = \(\frac{1}{2}\)
Question 2.
Given that p.d.f of a random variable X as follows
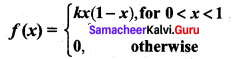
Find K and c.d.f.
Solution:


![]()
Question 3.
Suppose that the life in hours of a certain part of radio tube is an r.v X with p.d.f given by
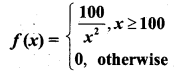
(i) What is the probability that all of three Such tubes in a given radio set will have to be replaced in the first 150 hours?
(ii) What is the probability that none of the three tubes will be replaced?
Solution:
(i) A tube in the radio set will have to be replaced during the first 150 hours if its life is less than 150 hours. Hence the required probability is
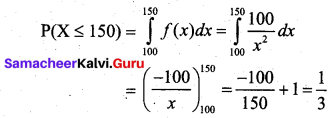
The probability that all three of the original tubes will have to be replaced during the first 150 hours is \(\left(\frac{1}{3}\right)^{3}=\frac{1}{27}\)
(ii) The probability that a tube is not replaced is given by P(X > 150)
= 1 – P(X ≤ 150)
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
Hence the probability that none of the three tubes will be replaced during the 150 hours of operation is \(\left(\frac{2}{3}\right)^{3}=\frac{8}{27}\)
Question 4.
Let X be a continuous random variable with p.d.f:
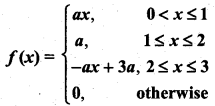
(i) Find ‘a’
(ii) compute P(X ≤ 1.5)
Solution:

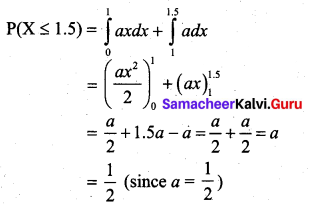
![]()
Question 5.
A random variable X has the probability function as follows:

Find E(3X + 1), E(X2) and Var(X).
Solution:
E(X) = (-1) (0.2) + 0(0.3) + 1(0.5) = -0.2 + 0.5 = 0.3
So E(3X + 1) = 3 E(X) + 1 = 3(0.3) + 1 = 1.9
E(X2) = (-1)2 (0.2) + 02 (0.3) + 12 (0.5) = 0.2 + 0.5 = 0.7
Var(X) = E(X2) – [E(X)]2 = 0.7 – (0.3)2 = 0.61
Question 6.
A player tossed two coins. If two heads show he wins Rs.4. If one head shows he wins Rs.2, but if two tails show he must pay Rs.3 as a penalty. Calculate the expected value of ‘ the sum won by him.
Solution:
Let X be the discrete random variable denoting the sum won by the player. We know that,
Probability of getting 2 heads = \(\frac{1}{4}\)
Probability of getting 1 head is \(\frac{1}{2}\)
Probability of getting 2 tail is \(\frac{1}{4}\)
So the player wins Rs.4 with probability \(\frac{1}{4}\), he wins Rs. 2 with probability \(\frac{1}{2}\) and loses Rs.3 with probability \(\frac{1}{4}\)
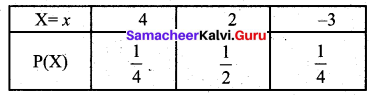
E(X) = 4(\(\frac{1}{4}\)) + 2(\(\frac{1}{2}\)) – 3(\(\frac{1}{4}\))
= 1 + 1 – \(\frac{3}{4}\)
= \(\frac{5}{4}\)
Thus the expected value of the sum won by him is Rs.1.25.