Students can download 12th Business Maths Chapter 6 Random Variable and Mathematical Expectation Miscellaneous Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Miscellaneous Problems
Question 1.
The probability function of a random variable X is given by
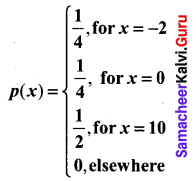
Evaluate the following probabilities.
(i) P(X ≤ 0)
(ii) P(X < 0)
(iii) P(|X| ≤ 2)
(iv) P(0 ≤ X ≤ 10)
Solution:
(i) P(x ≤ 0) = P( x = -2) + P(x = 0)
= \(\frac { 1 }{4}\) + \(\frac { 1 }{4}\) = \(\frac { 2 }{4}\) = \(\frac { 1 }{2}\)
(ii) P(x < 0) = P(x = -2) = \(\frac { 1 }{4}\)
(iii) P(|x| ≤ 2) = P(-2 ≤ X ≤ 2)
= P(X = -2) + P(X = 0) = \(\frac { 1 }{4}\) + \(\frac { 1 }{4}\)
= \(\frac { 2 }{4}\) = \(\frac { 1 }{2}\)
(iv) p(0 ≤ X ≤ 10) = P (X = 0) + P(X = 10)
= \(\frac { 1 }{4}\) + \(\frac { 1 }{2}\) = \(\frac { 1+2 }{4}\) = \(\frac { 3 }{4}\)
Question 2.
Let X be a random variable with a cumulative distribution function.
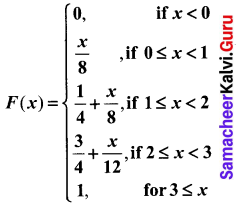
(a) Compute: (i) P(1 ≤ X ≤ 2) and (ii) P(X = 3).
(b) Is X a discrete random variable? Justify your answer.
Solution:
(a) (i) P(1 ≤ X ≤ 2) = F(2) – F(1)

(a) (ii) P(X = 3) = 0. The given random variable is continuous r.v.
Hence the probability for a particular value of X is zero.
(b) X is not discrete since the cumulative distribution function is a continuous function. It is not a step function.
![]()
Question 3.
The p.d.f. of X is defined as
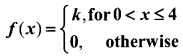
Find the value of k and also find P(2 ≤ X ≤ 4).
Solution:

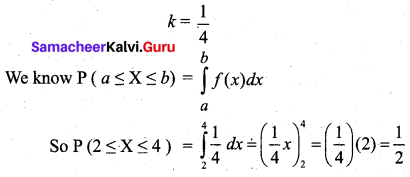
Question 4.
The probability distribution function of a discrete random variable X is
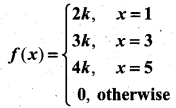
where k is some constant.
Find (a) k and (b) P(X > 2).
Solution:
(a) Given X is a discrete random variable.
The probability distribution can be written as
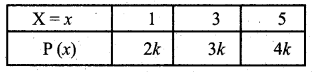
We know that Σp(x) = 1
⇒ 2k + 3k + 4k = 1
⇒ 9k = 1
⇒ k = 1/9
(b) P(X > 2) = P(X = 3) + P(X = 5)
= 3k + 4k
= 7k
= \(\frac{7}{9}\)
![]()
Question 5.
The probability density function of a continuous random variable X is
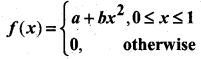
where a and b are some constants.
Find (i) a and b if E(X) = \(\frac{3}{5}\)
(ii) Var(X)
Solution:
Given that X is a continuous random variable and f(x) is a density function.



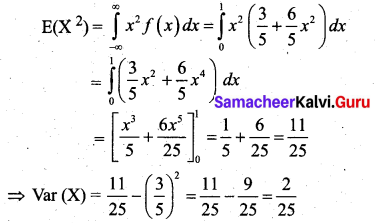
Question 6.
Prove that if E(X) = 0, then V(X) = E(X2).
Solution:
V(X) = E(X²) – [E(X)]²
= E(X²) – 0 {Given that E(X) = 0}
Var(X) = E(X²)
Hence proved.
![]()
Question 7.
What is the expected value of a game that works as follows: I flip a coin and if tails pay you ₹ 2; if heads pay you ₹ 1. In either case, I also pay you ₹ 50.
Solution:
Let X be the expected value of the game.
The probability distribution is given by,

Question 8.
Prove that
(i) V(aX) = a2 V(X)
(ii) V(X + b) = V(X)
Solution:
(i) LHS = V(ax)
= E(ax)² – [E(ax)]²
= a² E(x²) – [aE(x)]²
= a²E(x²) – a²E(x)]²
= a²E(x²) – E(x)²]
= a²v(x)
= RHS
Hence proved
(ii) LHS = V(x + b)
= E (x + b)² – [E(x + b)]²
= E(x² + 2bx + b²) – [E(x) + b]² –
= E(x²) + 2bE(x) + b² – [E(x)]² + b² + 2bE(x)]
= E(x²) + 2bE(x) + b² -[E(x)]² + b² – 2bE(x)]
= E(x²) – [E(x)]²
= V(x)
= RHS
LHS = RHS Hence proved.
![]()
Question 9.
Consider a random variable X with p.d.f
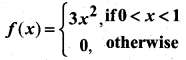
Find E(X) and V(3X – 2).
Solution:
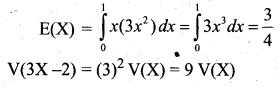
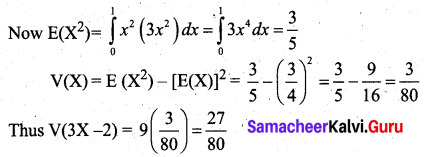
![]()
Question 10.
The time to failure in thousands of hours of an important piece of electronic equipment used in a manufactured DVD player has the density function.
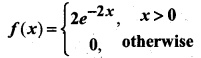
Find the expected life of this piece of equipment.
Solution:
Let X be the random variable denoting the life of the piece of equipment.

Thus the expected life of the piece of equipment is \(\frac{1}{2}\) hrs (in thousands).