Students can download 12th Business Maths Chapter 7 Probability Distributions Ex 7.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Ex 7.2
Question 1.
Define Poisson distribution.
Solution:
Poisson distribution is a discrete frequency distribution which gives the probability of a number of independent events occurring in a fixed time. It is useful for characterizing events with very low probabilities of occurrence within some definite time or space.
Question 2.
Write any 2 examples for Poisson distribution.
Solution:
1. The number of alpha particles emitted by a radioactive substance in a fraction of a second.
2. Number of road accidents occurring at a particular interval of time per day.
![]()
Question 3.
Write the conditions for which the Poisson distribution is a limiting case of the binomial distribution.
Solution:
Poisson distribution is a limiting case of binomial distribution under the following conditions:
- the number of trials ‘n’ is indefinitely large i.e, → ∞
- the probability of success ‘p’ in each trial is very small, i.e, p → 0
- np = λ is finite. Thus p = \(\frac{\lambda}{n}\) and q = 1 – \(\frac{\lambda}{n}\), λ > 0
Question 4.
Derive the mean and variance of the Poisson distribution.
Solution:
Let X be a Poisson random variable with parameter λ. The p.m.f is given by


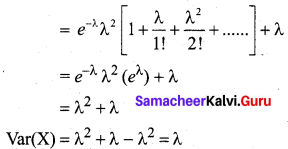
Thus the mean and variance of Poisson distribution are both equal to λ.
![]()
Question 5.
Mention the properties of Poisson distribution.
Solution:
Poisson distribution is the only distribution in which the mean and variance are equal.
Question 6.
The mortality rate for a certain disease is 7 in 1000. What is the probability for just 2 deaths on account of this disease in a group of 400? [Given e-2.8 = 0.06]
Solution:
Let X denote the number of deaths due to the disease
P(death) = \(\frac{7}{1000}\) = 0.007 ⇒ p = 0.007 and n = 400
The value of mean λ = np = (0.007) (400) = 2.8
Hence X follows a Poisson distribution with
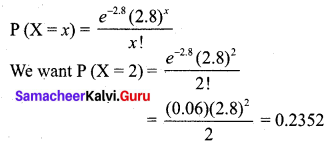
So the probability of just 2 deaths on account of this disease in a group of 400 is 0.2352.
![]()
Question 7.
It is given that 5% of the electric bulbs manufactured by a company are defective. Using Poisson distribution find the probability that a sample of 120 bulbs will contain no defective bulb.
Solution:
p(defective bulbs) = \(\frac { 5 }{100}\)
n = 120
The value of mean λ = np = 120 × \(\frac { 5 }{100}\)
λ = 6
Hence, x follows possion distribution with
P(x) = \(\frac { e^{-λ}λ^x }{x!}\)
(x = 0) = \(\frac { e^{-6}(6)^0 }{0!}\) = e-6
= 0.0025
Question 8.
A car hiring firm has two cars. The demand for cars on each day is distributed as a Poisson variate, with a mean of 1.5. Calculate the proportion of days on which
(i) Neither car is used
(ii) Some demand is refused.
Solution:
Let X be the Poisson variable denoting the demand for the cars.
It is given that mean is 1.5 ⇒ λ = 1.5
(i) P (Neither car is used) = P (X = 0) = \(\frac{e^{-1.5}(1.5)^{0}}{0 !}=e^{-1.5}=0.2231\)
(ii) Some demand is refused when demand is more than 2 since the firm has only 2 cars. So we want P (X > 2)
Now P (X > 2) = 1 – P (X ≤ 2)
= 1 – [P(X = 2) + P(X = 1) + P(X = 0)]

![]()
Question 9.
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be
(i) no phone at all
(ii) exactly 3 calls
(iii) at least 5 calls.
Solution:
Let X be the Poisson variable denoting the number of phone calls per minute.

P (X = 1) = \(\frac{e^{-2.5}(2.5)}{1 !}\) = (0.08208) (2.5) = 0.2052
Using the above values and P (X = 0) and P (X = 3) from the previous subdivisions in (A) we get,
P(X ≥ 5) = 1 – [0.1336 + 0.2138 + 0.2565 + 0.2052 + 0.08208]
= 1 – 0.89118
= 0.10882
Question 10.
The distribution of the number of road accidents per day in a city is Poisson with mean 4. Find the number of days out of 100 days when there will be
(i) no accident
(ii) at least 2 accidents and
(iii) at most 3 accidents.
Solution:
Let X be the Poisson variable denoting the number of accidents per day.
Given that mean is 4 (i.e,) λ = 4. The p.m.f is given by P(X = x) = \(\frac{e^{-4} 4^{x}}{x !}\)
(i) P (no accident) = P(X = 0) = e-4 = 0.0183
For 100 days we have 100 × 0.0183 = 1.83 ~ 2
Hence out of 100 days there will be no accident for 2 days.
(ii) P (atleast 2 accidents) = P (X ≥ 2)
= 1 – P (X < 2)
= 1 – [P(X = 1) + P(X = 0)]
= 1 – [e-4 (4) + e-4]
= 1 – (0.0183) (5)
= 1 – 0.0915
= 0.9085
For 100 days we have 100 × 0.9085 ~ 91
Hence out of 100 days there will be at least 2 accidents for 91 days.
(iii) P (atmost 3 accidents) = P (X ≤ 3)
= P (X = 0 ) + P (X = 1 ) + P (X = 2) + P (X = 3)
= \(e^{-4}\left[1+\frac{4}{1}+\frac{16}{2}+\frac{64}{6}\right]\)
= (0.0183) [23.6667]
= 0.4331
For 100 days we have 100 × 0.4331 ~ 43
Hence out of 100 days, there will be at most 3 accidents for 43 days.
![]()
Question 11.
Assuming that a fatal accident in a factory during the year is 1/1200, calculate the probability that in a factory employing 300 workers there will be at least two fatal accidents in a year, (given e-0.25 = 0.7788).
Solution:
Let X denote the number of accidents.
Given that probability of accidents ‘p’ is 1/1200 and n = 300

= 1 – [e-0.25 + e-0.25 (0.25)]
= 1 – e-0.25 (1.25)
= 1 – (0.7788) (1.25)
= 0.0265
Thus the probability that there will be atleast two fatal accidents in a year is 0.0265.
Question 12.
The average number of customers, who appear in a counter of a certain bank per minute is two. Find the probability that during a given minute
(i) No customer appears
(ii) three or more customers appear.
Solution:
Let X denote the number of customers.
Given λ = 2
(i) P (no customer) = P (X = 0)
= \(\frac{e^{-2}(2)^{0}}{0 !}\)
= e-2
= 0.1353
(ii) P (3 or more customers) = P (X ≥ 3)

Thus during a given minute, the probability that three or more customers appear is 0.3235.