Samacheer Kalvi 12th Business Maths Solutions Chapter 8 Sampling Techniques and Statistical Inference Miscellaneous Problems

Students can download 12th Business Maths Chapter 8 Sampling Techniques and Statistical Inference Miscellaneous Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 8 Sampling Techniques and Statistical Inference Miscellaneous Problems

Question 1.
Explain the types of sampling.
Solution:
There are two types of sampling. They are
(1) Non-Random sampling or Non-probability sampling
(2) Random sampling or probability sampling Random sampling refers to the selection of samples from the population in a random manner. A random sample is one where each and every item in the population has an equal chance of being selected.

“Every member of a parent population has had equal chances of being included “Dr. Yates.

“A random sample is a sample selected in such a way that every item in the population has an equal chance of being included”-Harver.

The different types of probability sampling are

• sampling random sampling
• stratified random sampling
• systematic sampling

Question 2.
Write a short note on sampling distribution and standard error.
Solution:
Sampling distribution: The sampling distribution of a statistic is the frequency distribution which is formed with various values of a statistic computed from different samples of the same size drawn from the same population.
For instance if we draw a sample of size n from a given finite population of size N, then the total number of possible samples is \(^{\mathrm{N}} C_{n}=\frac{\mathrm{N} !}{n !(N-n) !}=k\) (say). For each of these k samples we can compute some statistic, t = t(x₁, x₂, x₃ ,… x_n), in particular the mean \(\bar{X}\) the variance S², etc., is given below

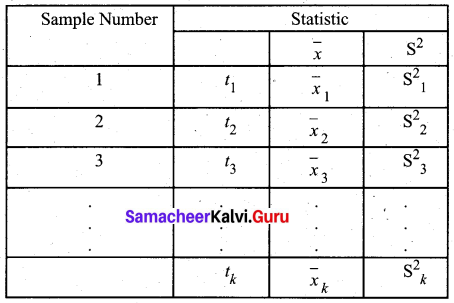
The set of the values of the statistic so obtained, one for each sample constitutes the sampling distribution of the statistic.

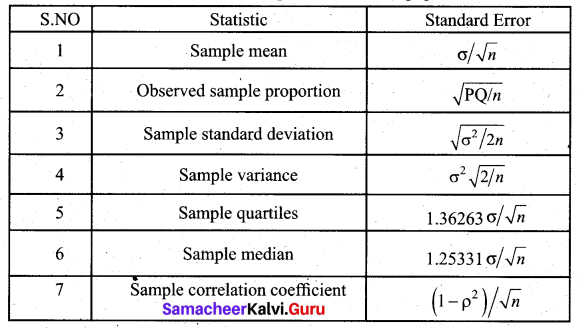
Standard Error:
The standard deviation of the sampling distribution of a statistic is known as its Standard Error abbreviated as S.E. The Standard Errors (S.E.) of some of the well-known statistics, for large samples, are given below, where n is the sample size, σ² is the population variance.

Question 3.
Explain the procedures of testing of hypothesis.
Solution:
Hypothesis testing addresses the important question of how to choose among alternative propositions while controlling and minimizing the risk of wrong decisions. A hypothesis which is tested for possible rejection is called null hypothesis H₀ and the hypothesis which is opposite to this is the alternative hypothesis H₁. There are two basic types of decision problems that can be considered in a hypothesis testing procedure.
(a) whether a population parameter has changed from or differs from a particular value.
(b) whether the sample has come from the population that has a parameter value less than or more than the hypothesized value.

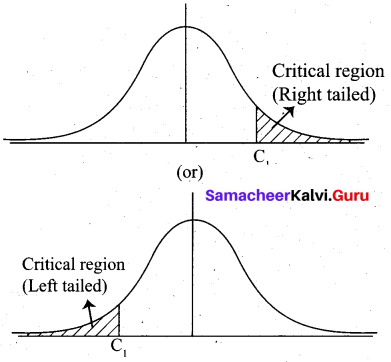
The set of all possible values of the sample statistic is referred to as the sample space. The test procedure divides the sample space into two parts called the acceptance region and rejection region (critical region). In the case of the two-tailed test, we find two values C₁ and C₂ which set the limits on the amount of sampling variation consistent with the null hypothesis H₀. For the one-tailed test, we find only one value C₁

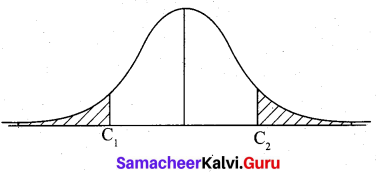
When the hypothesis H₀ is rejected when it is true the error is Type I error. When H0 is accepted when it is false it is called Type II error. When the calculated value of the test statistic is less than the table value, we accept the null hypothesis H₀; otherwise, accept alternative hypothesis H₁.

Question 4.
Explain in detail the test of significance of a single mean.
Solution:
A random sample of size n (n ≥ 30) is drawn from a population. We want to test the population mean has a specified value µ₀.
Procedure for testing: (For two-tail test)
The null hypothesis is H₀ : µ = µ₀.
The alternative hypothesis is H₁ : µ ≠ µ₂
Since n is large the sampling distribution of \(\bar{x}\) (the sample mean) is approximately normal.
The test statistic

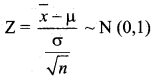
For a significance level α = 0.05 (5% level)
If |Z| < 1.96, H0 is accepted at 5% level. If |Z| > 1.96, H₀ is rejected at 5% level
For α = 0.01 (1% level), if |Z| < 2.58, H₀ is accepted. If |Z| > 2.58, H₀ is rejected.
Procedure for one tail test: (left tail)
H₀ : µ ≥ µ₀
H₁ : µ < µ₀
At α = 0.05, |Z| = 1.645
If Z < -1.645, H₀ is rejected If Z > -1.645, H₀ is accepted
One tail test: (right tail)
If Z < 1.645, H₀ is accepted If Z > 1.645, H₀ is rejected at 5% level of significance.

Question 5.
Determine the standard error of proportion for a random sample of 500 pineapples was taken from a large consignment and 65 were found to be bad.
Solution:
The standard error of proportion is S.E. = \(\sqrt{\mathrm{PQ} / \mathrm{n}}\)
Given sample size n = 500 and P = \(\frac{65}{500}\)

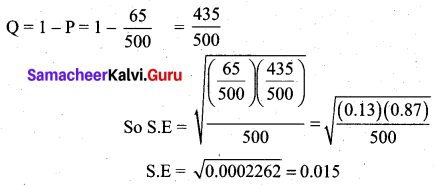
Question 6.
A sample of 100 students is drawn from a school. The mean weight and variance of the sample are 67.45 kg and 9 kg. respectively. Find (a) 95% (b) 99% confidence intervals for estimating the mean weight of the students.
Solution:
Given Sample size n = 100
Sample mean \(\bar{x}\) = 67.45 kg
Sample S.D s = √9 = 3 kg
(a) 95% confidence interval for population mean µ is,


Therefore 99% confidence intervals for estimating the mean weight of the students is (66.68, 68.22)

Question 7.
The mean I.Q of a sample of 1600 children was 99. Is it likely that this was a random sample from a population with a mean I.Q 100 and standard deviation of 15? (Test at 5% level of significance)
Solution:
Given
n (Sample size) = 1600 children
\(\bar{x}\) (Sample mean) = 99
µ (Population mean) = 100
σ (Population SD) = 15
α (Level of significance) = 5%
Null hypothesis H₀ : µ = 100
(Sample has been drawn from a population with mean 100 and S.D 15)
Alternative hypothesis H₁ : µ ≠ 100
(Sample has not been taken from a population with mean 100 and S.D 15)
Test statistic

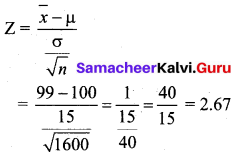
The significant value or table value \(Z_{\alpha / 2}\) = 1.96. Comparing the values, we see that 2.67 > 1.96 (or) Z > \(Z_{\alpha / 2}\) at 5% level of significance. So the null hypothesis is rejected. Hence we conclude that the random sample is not taken from a population with mean I.Q = 100 and S.D = 15.