Students can download 12th Business Maths Chapter 9 Applied Statistics Ex 9.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 9 Applied Statistics Ex 9.2
Question 1.
Define Index Number.
Solution:
Index Numbers are the indicators which reflect the changes over a specified period of time in the price of different commodities, production, sales, cost of living etc.
“An Index Number is a device which shows by its variations the change in a magnitude which is not capable of accurate measurements in itself or of direct valuation in practice”. – Wheldon
“An Index number is a statistical measure of fluctuations in a variable arranged in the form of a series and using a base. Period for maxing H comparisons” – Lawrence J Kaplan.
Question 2.
State the uses of Index Number.
Solution:
The uses of Index number are as given below:
- It is an important tool for formulating decision and management policies.
- It helps in studying the trends and tendencies.
- It determines the inflation and deflation in an economy
![]()
Question 3.
Mention the classification of Index Number.
Solution:
Index number can be classified as follows,
(i) Price Index Number:
It measures the general changes in the retail or wholesale price level of a particular or group of commodities.
(ii) Quantity Index Number:
These are indices of measure the changes in the number of goods manufactured in a factory.
(iii) Cost of living Index Number:
These are intended to study the effect of change in the price level on the cost of living of different classes of people.
Question 4.
Define Laspeyre’s price index number
Solution:
The weighted aggregate index number using base period weights is called Laspeyre’s price index number.

Where p1 is current year price
p0 is base year price
q0 is base year quantity
![]()
Question 5.
Explain Paasche’s price index number.
Solution:
If both prices and quantities were permitted to change, then it is impossible to isolate the part of movement due to price changes alone. In this case, the current year quantities appear more realistic weights than the base year quantities. The index number based on current year quantities is called Paasche’s price index number.
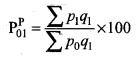
Where p1 is the current year price
q1 is the current year quantity
p0 is the base year price
Question 6.
Write a note on Fisher’s price index number.
Solution:
Fisher defined a weighted index number as the geometric mean of Laspeyre’s index number and Paasche’s Index number
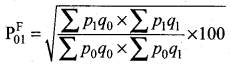
The Fisher-price index number is also known as the “ideal” price index number. This requires more data than the other two index numbers and as a result, may often be impracticable. But this is a good index number because it satisfies both the time-reversal test and factor reversal test.
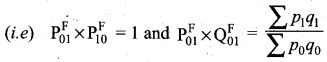
![]()
Question 7.
State the test of the adequacy of the index number.
Solution:
Index numbers are studied to know the relative changes in price and quantity for any two years compared. There are two tests which are used to test the adequacy of an index number. The two tests are as follows
- Time Reversal Test
- Factor Reversal Test
The criterion for a good index number is to satisfy the above two tests.
Question 8.
Define Time Reversal Test.
Solution:
It is an important test for testing the consistency of a good index number. This test maintains time consistency by working both forward and backward with respect to time (here time refers to the base year and current year). Symbolically the following relationship should be satisfied, P01 × P10 = 1
Fisher’s index number formula satisfies the above relationship

when the base year and current year are interchanged, we get,
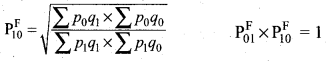
![]()
Question 9.
Explain Factor Reversal Test.
Solution:
Factor Reversal Test:
This is another test for testing the consistency of a good index number. The product of price index number and quantity index number from the base year to the current year should be equal to the true value ratio. That is the ratio between the total value of the current period and the total value of the base period is known as the true value ratio. Factor Reversal Test is given by,
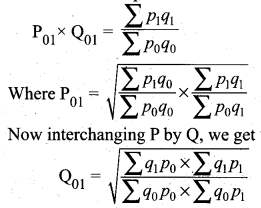
where P01 is the relative change in price.
Q01 is the relative change in quantity.
Question 10.
Define true value ratio.
Solution:
\(\frac { Σp_1q_1 }{Σp_0q_0}\) is the ratio of the total value in the current period to the total value in the base period and this ratio is called the true value ratio.
![]()
Question 11.
Discuss Cost of Living Index Number.
Solution:
Cost of Living Index Number is constructed to study the effect of changes in the price of goods and services of consumers for a current period as compared with the base period. The change in the cost of living index number between any two periods means the change in income which will be necessary to maintain the same standard of living in both periods. Therefore the cost of living index number measures the average increase in the cost to maintain the same standard of life.
Further, the consumption habits of people differ widely from class to class (rich, poor, middle class) and even with the region. The changes in the price level affect the different classes of people, consequently, the general price index numbers fail to reflect the effect of changes in their cost of living in different classes of people. Therefore, the cost of living index number measures the general price movement of the commodities consumed by different classes of people.
Question 12.
Define Family Budget Method.
Solution:
In this method, the weights are calculated by multiplying the prices and quantity of the base year.
(i.e.) V = Σp0q0. The formula is given by,
Cost of Living Index Number = \(\frac { Σpv }{Σv}\)
where P = \(\frac { p_1 }{p_0}\) × 100 is the price relative.
v = Σp0q0 is the value relative.
![]()
Question 13.
State the uses of the Cost of Living Index Number.
Solution:
Uses of Cost of Living Index Number
- It indicates whether the real wages of workers are rising or falling for a given time.
- It is used by the administrators for regulating dearness allowance or grant of bonus to the workers.
Question 14.
Calculate by a suitable method, the index number of price from the following data:
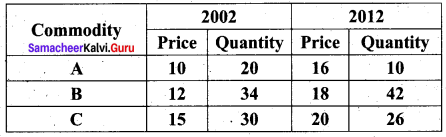
Solution:

The Laspeyres price index number
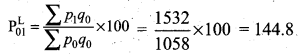
Paasche’s price index number
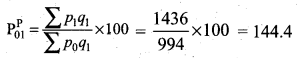
On average, there is an increase of 44.8% and 44.4% in the price of the commodities by Laspeyres and Paasche’s price index number respectively for the current year 2012 as compared with the base year 2002.
![]()
Question 15.
Calculate price index number for 2005 by (a) Laspeyre’s (b) Paasche’s method.
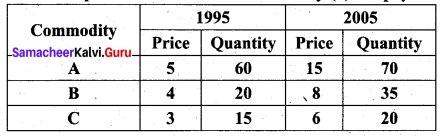
Solution:

Laspeyre’s price index number
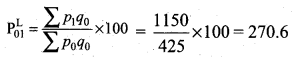
Paasche’s price index number
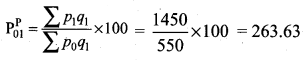
On an average, there is an increase of 170.6% and 163.63% in the price of the commodities by Laspeyre’s and Paasche’s price index number respectively for the current year 2005 as compared with the base year 1995.
Question 16.
Compute (i) Laspeyre’s (ii) Paasche’s (iii) Fisher’s Index numbers for 2010 from the following data.
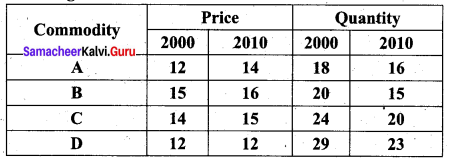
Solution:
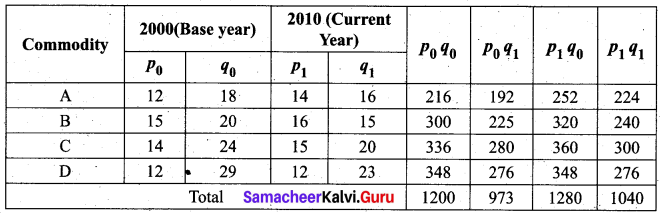
Laspeyre’s price index number
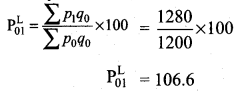
Paasche’s price index number

Fisher’s price index number

On average, there is an increase of 6.6%, 6.8%, and 6.7% in the price of the commodities by Laspeyres, Paasche’s, and Fisher’s index number respectively for the current year 2010 as compared to the base year 2000.
![]()
Question 17.
Using the following data, construct Fisher’s Ideal index and show how it satisfies Factor Reversal Test and Time Reversal Test?
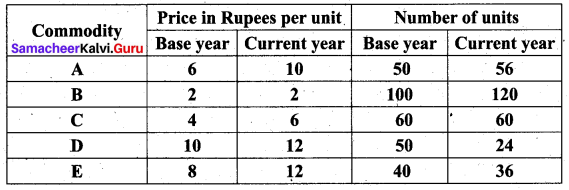
Solution:
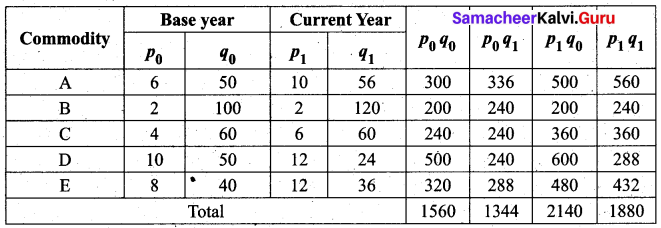
Fisher’s ideal index

Time reversal test:
To prove P01 × P10 = 1
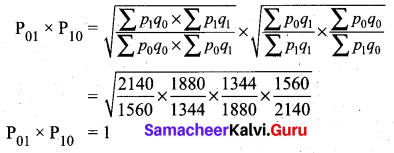
Time reversal test is satisfied.
Factor Reversal Test:
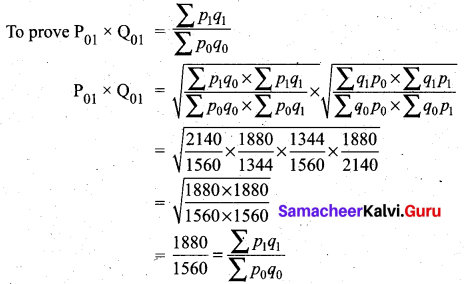
Factor Reversal Test is satisfied.
Question 18.
Using Fisher’s Ideal Formula; compute price index number for 1999 with 1996 as the base year, given the following.
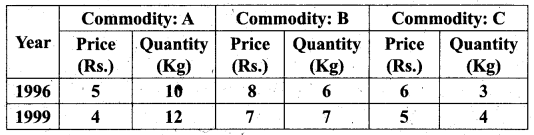
Solution:
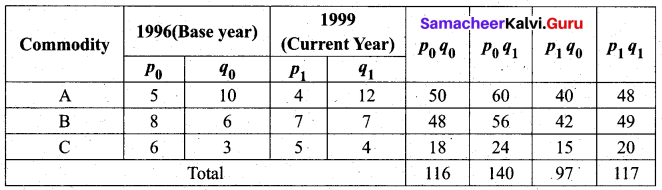
Fisher’s index number

Thus we interpret that on an average, there is a decrease of 16.41 % in the price of commodities by Fisher’s Index number for the current year 1999 as compared to the base year 1996.
![]()
Question 19.
Calculate Fisher’s index number to the following data. Also, show that satisfies Time Reversal Test.
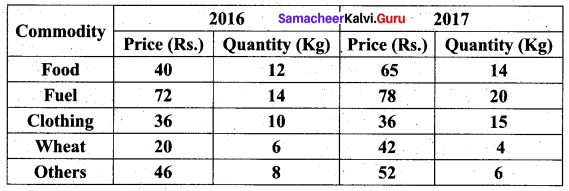
Solution:
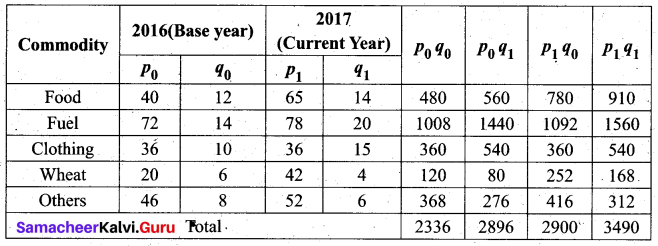
Fisher’s price index number

On average, there is an increase of 22.3% in the price of commodities by Fisher’s Index number for the current year 2017 as compared to the base year 2016
Time reversal test:
To prove P01 × P10 = 1

Time reversal test is satisfied.
Question 20.
The following are the group index numbers and the group weights of an average working-class family’s budget. Construct the cost of living index number:

Solution:
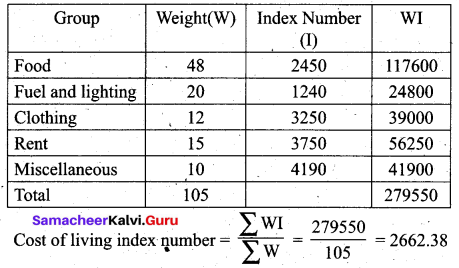
Question 21.
Construct the cost of living Index number for 2015 on the basis of 2012 from the following data using the family budget method.
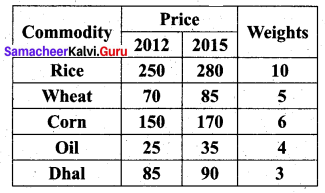
Solution:
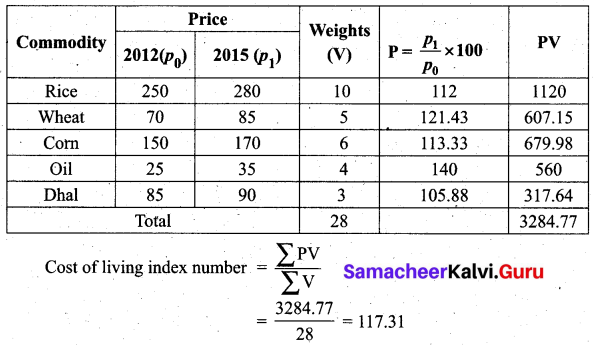
Hence, the cost of living index number for a particular class of people for the year 2015 is increased by 17.31% as compared to the year 2012.
![]()
Question 22.
Calculate the cost of living index by aggregate expenditure method:
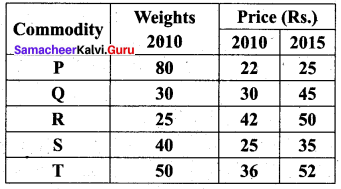
Solution:
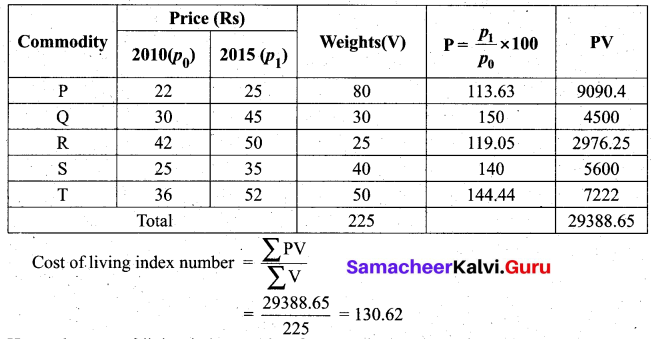
Hence, the cost of living index number for a particular class of people for the year 2015 is increased by 30.62% as compared to the year 2010.