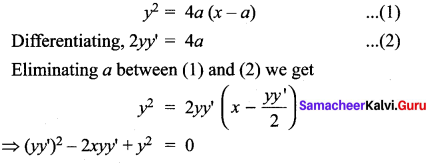You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.3
Question 1.
Find the differential equation of the family of
(i) all non-vertical lines in a plane
Solution:
Equation of family of all non-vertical lines is
y = mx + c (m ≠ 0)
Differentiate with respect to ‘x’
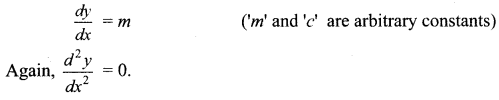
(ii) all non-horizontal lines in a plane.
Solution:
Equation of family of all non-horizontal lines is
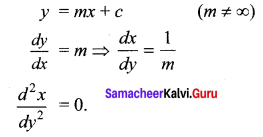
![]()
Question 2.
Form the differential equation of all straight lines touching the circle x2 + y2 = r2
Solution:
Equation of circle x2 + y2 = r2 of the line y = mx + c is to be a tangent to the circle, then the equation of the tangent is
![]()
Differentiating with respect to V dy

Question 3.
Find the differential equation of the family of circles passing through the origin and having their centres on the x -axis.
Solution:
All circles passing through the origin and having their centre on the x -axis say at (a, 0) will have radius ‘a’ units.
∴ Equation of circle is (x – a2) + y2 = a2 ….(1) [ ∵ ‘a’ arbitrary constant]
Differentiate with respect to ‘x’

![]()
Question 4.
Find the differential equation of the family of all the parabolas with latus rectum 4a and whose axes are parallel to the x -axis.
Solution:
Equation of all parabolas whose axis is parallel to X – axis is
(y – k)2 = 4a (x – h)
Where (h, k) is the vertex

Question 5.
Find the differential equation of the family of parabolas with vertex at (0, -1) and having axis along the y – axis.
Solution:
Given, vertex (0, -1) and axis along y-axis
Equation of Parabola, (x + 1)2 = – 4ay …… (1) [∵ a is the perameter]
Differentiate with respect to ‘x’
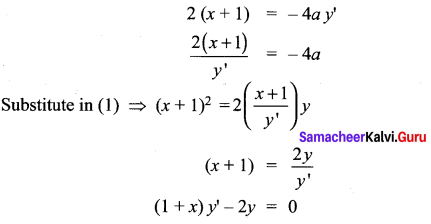
Question 6.
Find the differential equations of the family of all the ellipses having foci on the y – axis and centre at the origin.
Solution:
Equations of the family of all the Ellipses having foci on the y – axis and centre at the origin is
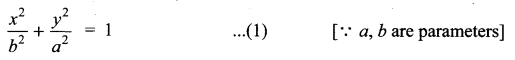
Differentiate with respect to ’x’
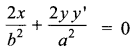

![]()
Question 7.
Find the differential equation corresponding to the family of curves represented by the equation y = Ae8x + Be-8x, where A and B are arbitrary constants.
Solution:

Question 8.
Find the differential equation of the curve represented by xy = aex + be-x + x2.
Solution:
xy = aex + be-x + x2
xy – x2 = aex + be-x …… (1) [∵ a’, b’ are arbitrary constants]
Differentiate with respect to ‘x’
xy’ +y – 2x = aex – be-x
Again, Differentiate with respect to ‘x’
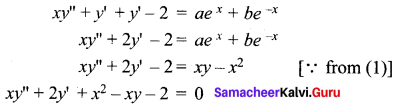
Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.3 Additional Problems
Question 1.
Find the differential equation of the family of straight lines y = mx + \(\frac{a}{m}\) when
(i) m is the parameter,
(ii) a is the parameter,
(iii) a, m both are parameters.
Solution:
![]()
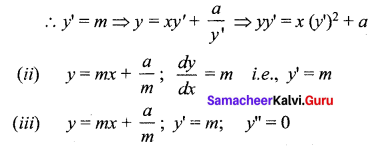
![]()
Question 2.
Find the differential equation that will represent family of all circles having centres on the x-axis and the radius is unity.
Solution:
Equation of a circle with centre on x-axis and radius 1 unit is
(x – a)2 + y2 = 1 ….. (1)
Differentiating with respect to x,
2 (x – a) + 2yy’ – 0
⇒ 2 (x – a) = – 2yy’
(or) x – a = -yy’ ……(2)
Substituting (2) in (1), we get,
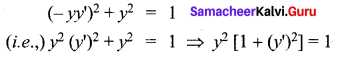
Question 3.
From the differential equation from the following equations.
(i) y = e2x (A + Bx)
Solution:
ye-2x = A + Bx ……. (1)
Since the above equation contains two arbitrary constants, differentiating twice,
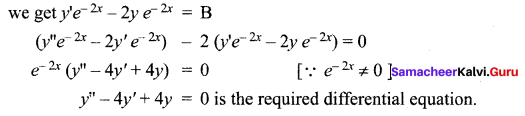
(ii) y = ex(A cos 3x + B sin 3x)
Solution:

![]()
(iii) Ax2 + By2 = 1
Solution:
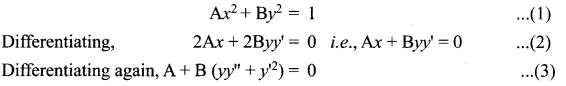
Eliminating A and B between (1), (2) and (3) we get
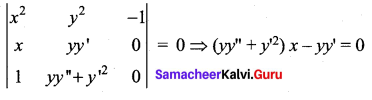
(iv) y2 = 4a(x – a)
Solution: