Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.6

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.6

Solve the following differential equations:

Question 1.

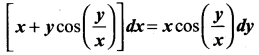
Solution:

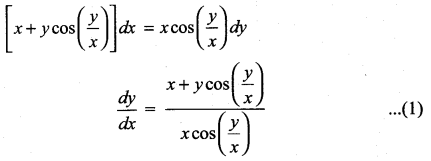
This is a Homogeneous differential equation

Seperating the variables

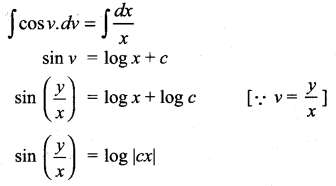
Question 2.
(x³ + y³) dy – x²y dx = 0
Solution:
(x³ + y³) dy – x²y dx = 0
(x³ + y³) dy = x³y dx

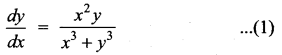
This is a Homogeneous differential equation.

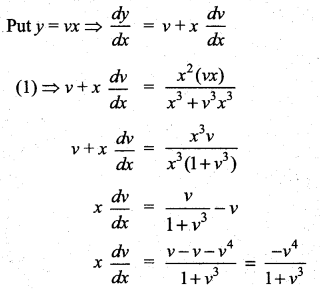
Separating the variables

Question 3.

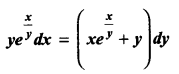
Solution:

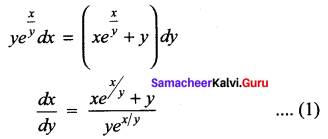
This is a Homogeneous differential equation

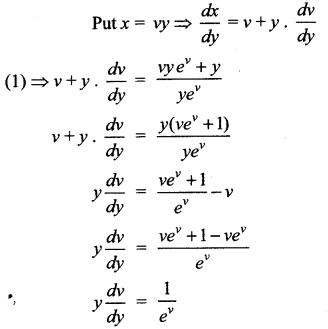
Seperating the variables

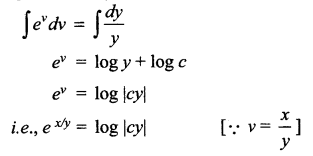
Question 4.
2xydx + (x² + 2y²) dy = 0
Solution:
2xy dx + (x² + 2y²) dy = 0
(x² + 2y²) dy = – 2xy dx

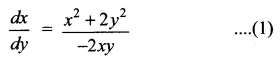
This is a Homogeneous differential equation


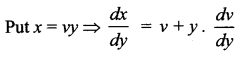
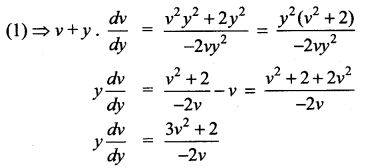
Separating the variables

Question 5.
(y² – 2xy)dx = (x² – 2xy)dy
Solution:
(y² – 2xy) dx = (x² – 2xy) dy

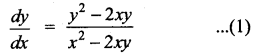
This is a Homogeneous differential equation


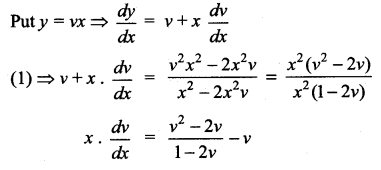
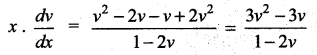
Seperating the variables

Question 6.

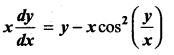
Solution:

Seperating the variables

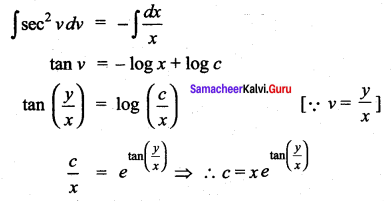
Question 7.

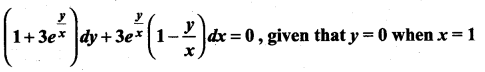
Solution:

This is a Homogeneous differential equation

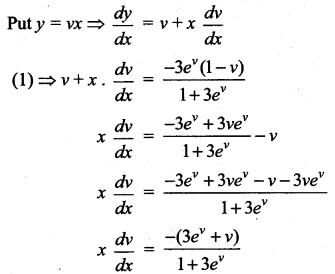
Separating the variables

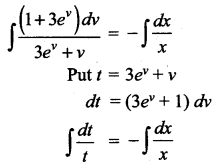
Question 8.
(x² + y²) dy = xy dx. It is given that y(1) = 1 and y(x₀) = e. Find the value of x₀.
Solution:

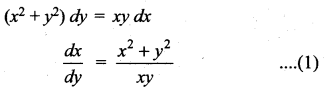
This is a Homogeneous differential equation

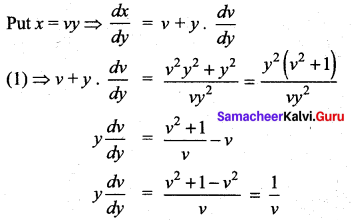
Seperating the variables

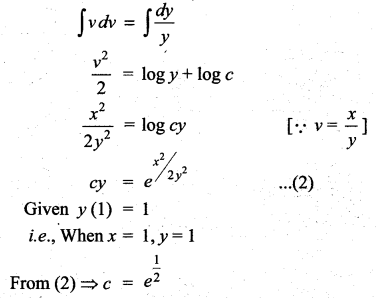
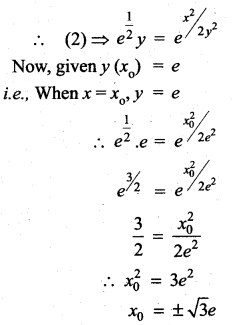
Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.6 Additional problems

Question 1.
Solve: (2\(\sqrt{x y}\))dy + y dx = 0
Solution:

Question 2.
Solve: (x³ + 3xy²)dx + (y³ + 3x²y)dy = 0
Solution:


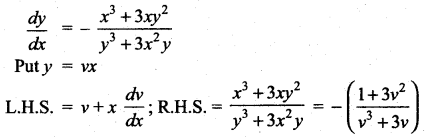
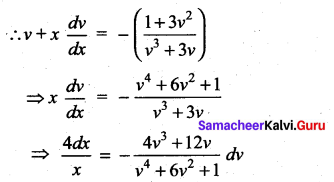
Integrating, we have

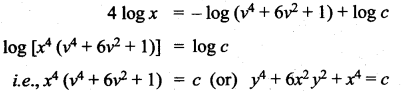
Question 3.

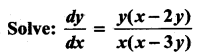
Solution:

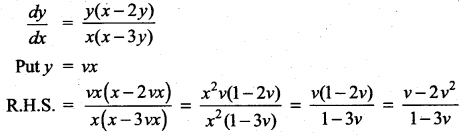
Which is in terms of v alone.
⇒ the given problem comes under homogeneous type.

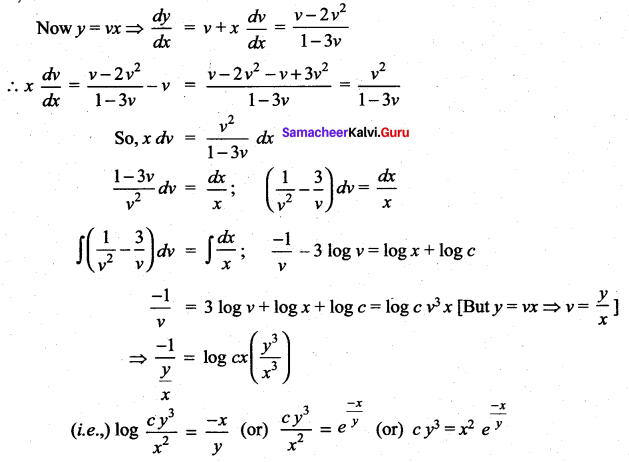
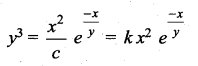
Question 4.
Solve: (x² + y²)dy = xy dx
Solution:

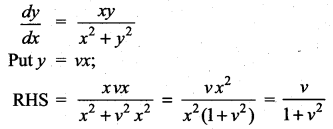
Which is a function in v alone.
⇒ the given problem comes under homogeneous type.

Question 5.
Find the equation of the curve passing through (1, 0) and which has slope \(1+\frac{y}{x}\) at (x, y).
Solution:


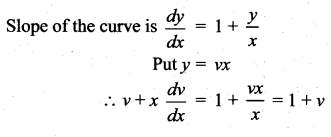
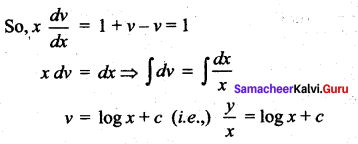
Given the curve passes through (1, 0) ⇒ at x = 1, y = 0
0 = log 1 +c ⇒ c = 0