You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 11 Probability Distributions Ex 11.2
Question 1.
Three fair coins are tossed simultaneously. Find the probability mass function for number of heads occurred.
Solution:
When three coins are tossed, the sample space is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
‘X’ is the random variable denotes the number of heads.
∴ ‘X’ can take the values of 0, 1, 2 and 3
Hence, the probabilities
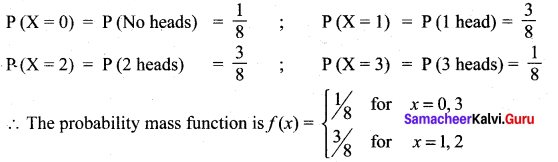
Question 2.
A six sided die is marked ‘1’ on one face, ‘3’ on two of its faces, and ‘5’ on remaining three faces. The die is thrown twice. If X denotes the total score in two throws, find
(i) the probability mass function
(ii) the cumulative distribution function
(iii) P(4 ≤ X < 10)
(iv) P( X ≥ 6)
Solution:
Given that die is marked ‘ 1 ’ on one face, ‘3’ on two of its faces and ‘5’ on remaining three faces. i.e., {1, 3, 3, 5, 5, 5} in a single die.
When it is thrown twice, the number of sample points is 36, in which the sum of faces numbers are 2, ,4, 6, 8 and 10 are the value of random variable ‘X’.
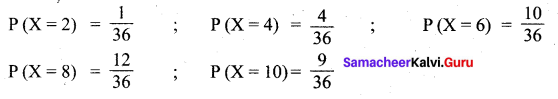
![]()
(i) Probability mass function:

(ii) The Cumulative distribution function:

(iii) (4 ≤ 10) = P(X = 4) + P(X = 6) + P(X = 8)
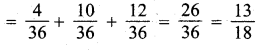
(iv) P(X ≥ 6) = P (X = 6) + P (X = 8) + P (X = 10)
![]()
Question 3.
Find the probability mass function and cumulative distribution function of number of girl child in families with 4 children, assuming equal probabilities for boys and girls.
Solution:
Let ‘X’ be the random variable which denotes the number of girl children in the family of 4 children and X takes the values of 0, 1, 2, 3, 4.
Probability of child being a boy = P (B) = \(\frac{1}{2}\)
Probability of child being a girl = P (G) = \(\frac{1}{2}\)


Question 4.
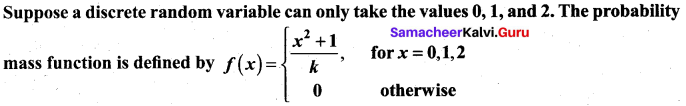
Find
(i) the value of k
(ii) cumulative distribution function
(iii) P(X ≥ 1).
Solution:

Question 5.
The cumulative distribution function of a discrete random variable is given by

Find the (i) the probability mass function
(ii) P(X < 1)
(iii) P(X ≥ 2)
Solution:

For x = -1, f(x) = 0.15 – 0 = 0.15
For x = 0, f(x) = 0.35 – 0.15 = 0.20
For x = 1, f(x) = 0.60 – 0.35 = 0.25
For x = 2, f(x) = 0.85 – 0.60 = 0.25
For x = 3, f(x) = 1 – 0.85 = 0.15
(i) Probability mass function table

(ii) P (X < 1) = P(X = -1) + P(X = 0) = 0.15 + 0.20 = 0.35
(iii) P (X ≥ 2) = P (X = 2) + P (X = 3) = 0.25 + 0.15 = 0.40
![]()
Question 6.
A random variable X has the following probability mass function.

Solution:
Given probability mass function

(i) We know that \(\Sigma P_{i}\) = 1
i.e., k2 + 2k2 + 3k2 + 2k + 3k = 1
6k2 + 5k = 1
6k2 + 5k – 1 = 0
(k + 1) (6k – 1) = 0
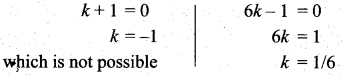
(ii) P (2 ≤ X < 5)
= P (X = 2) + P (X = 3) + P (X = 4)
= 2k2 + 3k2 + 2k = 5k2 + 2k
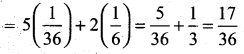
(iii) P (3 < X) = P (X > 3)
= P (X = 4) + P (X = 5) = 2k + 3k = 5k = 5/6
Question 7.
The cumulative distribution function of a discrete random variable is given by.

Find (i) the probability mass function
(ii) P(X < 3) and
(iii) P(X ≥ 2).
Solution:

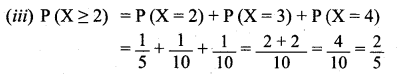
![]()
Samacheer Kalvi 12th Maths Solutions Chapter 11 Probability Distributions Ex 11.2 Additional Problems
Question 1.
Find the probability mass function, and the cumulative distribution function for getting ‘3’s when two dice are thrown.
Solution:
Two dice are thrown. Let X be the random variable of getting number of ‘3’s.
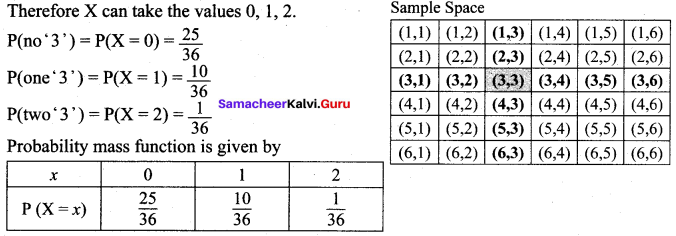
Cumulative distribution function:

Question 2.

Solution:

Question 3.

Solution:

![]()
Question 4.
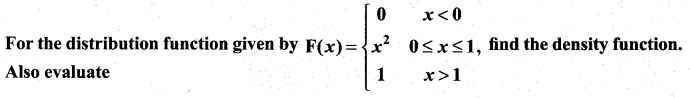
(i) P(0.5 < X < 0.75)
(ii) P(X ≤ 0.5)
(iii) P(X > 0.75)
Solution:

Question 5.
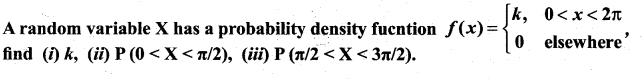
Solution:
