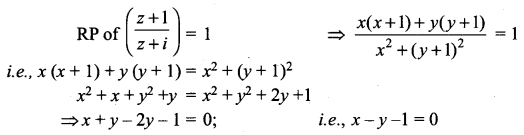You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.6
Question 1.
If z = x + iy is a complex number such that \(\left|\frac{z-4 i}{z+4 i}\right|=1\). show that the locus of z is real axis.
Solution:
\(\left|\frac{z-4 i}{z+4 i}\right|=1\)
⇒ |z – 4i| = |z + 4i|
let z = x + iy
⇒ |x + iy – 4i| = |x + iy + 4i|
⇒ |x + i(y – 4)| = |x +(y + 4)|
⇒ \(\sqrt{x^{2}+(y-4)^{2}}=\sqrt{x^{2}+(y+4)^{2}}\)
Squaring on both sides, we get
x2 + y2 – 8y + 16 = x2 + y2 + 16 + 8y
⇒ -16y = 0
⇒ y = 0 in two equation of real axis.
Question 2.
If z = x + iy is a complex number such that Im \(\left(\frac{2 z+1}{i z+1}\right)=0\) show that the locus of z is 2x2 + 2y2 + x – 2y = 0.
Solution:
Let z = x + iy

2x2 + 2y2 + x – 2y = 0.
Hence proved.
![]()
Question 3.
Obtain the Cartesian form of the locus of z = x + iy in each of the following cases:
(i) [Re(iz)]2 = 3
(ii) Im[(1 – i)z + 1] = 0
(iii) |z + i| = |z – 1|
(iv) \(\bar{z}=z^{-1}\)
Solution:
(i) z = x + iy
[Re(iz)]2 = 3
⇒ [Re[i(x + iy]]2 = 3
⇒ [Re(ix – y)]2 = 3
⇒ (-y)2 = 3
⇒ y2 = 3
(ii) Im[(1 – i)z + 1] = 0
⇒ Im [(1 – i)(z + iy) + 1] = 0
⇒ Im[x + iy – ix + y + 1] = 0
⇒ Im[(x + y + 1) + i(y – x)] = 0
Considering only the imaginary part
y – x = 0 ⇒ x = y
(iii) |z + i| = |z – 1|
⇒ |x + iy + i| = | x + iy – 1|
⇒ |x + i(y + 1)| = |(x – 1) + iy|
Squaring on both sides
|x + i(y + 1)|2 = |(x – 1) + iy|2
⇒ x2 + (y + 1)2 = (x – 1)2 + y2
⇒ x2 + y2 + 2y + 1 = x2 – 2x + 1 + y2
⇒ 2y + 2x = 0
⇒ x + y = 0
(iv) \(\bar{z}=z^{-1}\)
⇒ \(\bar{z}=\frac{1}{z}\)
⇒ \(z \bar{z}=1\)
⇒ |z|2 = 1
⇒ |x + iy|2 = 1
⇒ x2 + y2 = 1
Question 4.
Show that the following equations represent a circle, and, find its centre and radius.
(i) |z – 2 – i| = 3
(ii) |2z + 2 – 4i| = 2
(iii) |3z – 6 + 12i| = 8
Solution:
(i) Let z = x + iy
|z – 2 – i| = 3
⇒ |x + iy – 2 – i| = 3
⇒ |(x – 2) + i(y – 1)| = 3
⇒ \(\sqrt{(x-2)^{2}+(y-1)^{2}}=3\)
Squaring on both sides
(x – 2)2 + (y – 1)2 = 9
⇒ x2 – 4x + 4 + y2 – 2y + 1 – 9 = 0
⇒ x2 + y2 – 4x – 2y – 4 = 0 represents a circle
2g = -4 ⇒ g = -2
2f = -2 ⇒ f = -1
c = -4
(a) Centre (-g, -f) = (2, 1) = 2 + i
(b) Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{4+1+4}=3\)
Aliter: |z – (2 + i)| = 3
Centre = 2 + i
radius = 3
![]()
(ii) |2(x + iy) + 2 – 4i| = 2
⇒ |2x + i2y + 2 – 4i| =2
⇒ |(2x + 2) + i(2y – 4)| = 2
⇒ |2(x + 1) + 2i(y – 2)| = 2
⇒ |(x + 1) + i(y – 2)| = 1
⇒ \(\sqrt{(x+1)^{2}(y-2)^{2}}=1\)
Squaring on both sides,
x2 + 2x + 1 + y2 + 4 – 4y – 1 = 0
⇒ x2 + y2 + 2x – 4y + 4 = 0 represents a circle
2g = 2 ⇒ g = 1
2f = -4 ⇒ f = -2
c = 4
(a) Centre (-g, -f) = (-1, 2) = -1 + 2i
(b) Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{1+4-4}=1\)
Aliter: 2|(z + 1 – 2i)| = 2
|z – (-1 + 2i)| = 1
Centre = -1 + 2i
radius = 1
(iii) |3(x + iy) – 6 + 12i| = 8
⇒ |3x + i3y – 6 + 12i| = 8
⇒ |3(x – 2) + i3 (y + 4)| = 8
⇒ 3|(x – 2) + i (y + 4)| = 8
⇒ \(3 \sqrt{(x-2)^{2}+(y+4)^{2}}=8\)
Squaring on both sides,
9[(x – 2)2 + (y + 4)2] = 64
⇒ x2 – 4x + 4 + y2 + 8y + 16 = \(\frac{64}{9}\)
⇒ x2 + y2 – 4x + 8y + 20 – \(\frac{64}{9}\) = 0
x2 + y2 – 4x + 8y + \(\frac{116}{9}\) = 0 represents a circle.
2g = -4 ⇒ g = -2
2f = 8 ⇒ f = 4
c = \(\frac{116}{9}\)
(a) Centre (-g, -f) = (2, -4) = 2 – 4i
(b) Radius = \(=\sqrt{g^{2}+f^{2}-c}=\sqrt{4+16-\frac{116}{9}}=\sqrt{\frac{180-116}{9}}=\frac{8}{3}\)
Aliter:
|z – 2 + 4i| = \(\frac{8}{3}\)
⇒ |z – (2 – 4i)| = \(\frac{8}{3}\)
Centre = 2 – 4i, Radius = \(\frac{8}{3}\)
Question 5.
Obtain the Cartesian equation for the locus of z = x + iy in each of the following cases.
(i) |z – 4| = 16
(ii) |z – 4|2 – |z – 1|2 = 16
Solution:
(i) z = x + iy
|z – 4| = 16
⇒ |x + iy – 4| = 16
⇒ |(x – 4) + iy| = 16
⇒ \(\sqrt{(x-4)^{2}+y^{2}}=16\)
Squaring on both sides
(x – 4)2 + y2 = 256
⇒ x2 – 8x + 16 + y2 – 256 = 0
⇒ x2 + y2 – 8x – 240 = 0 represents the equation of circle
(ii) |x + iy – 4|2 – |x + iy – 1|2 = 16
⇒ |(x – 4) + iy|2 – |(x – 1) + iy|2 = 16
⇒ [(x – 4)2 + y2] – [(x – 1)2 + y2] = 16
⇒ (x2 – 8x + 16 + y2) – (x2 – 2x + 1 + y2) = 16
⇒ x2 + y2 – 8x + 16 – x2 + 2x – 1 – y2 = 16
⇒ -6x + 15 = 16
⇒ 6x + 1 = 0
Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.6 Additional Problems
Question 1.
If the imaginary part of 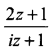 is -2, then show that the locus of the point representing z in the argand plane is a straight line.
is -2, then show that the locus of the point representing z in the argand plane is a straight line.
Solution:
Let z = x + iy. Then,
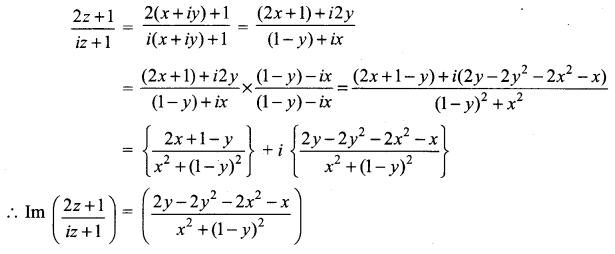
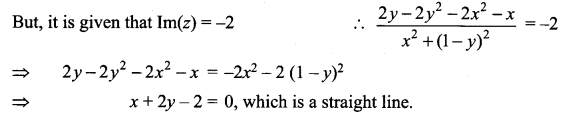
Hence, the locus of z is a straight line
Question 2.
If the real part of ![]() is 4, then show that locus of the point representing z in the complex plane is a circle.
is 4, then show that locus of the point representing z in the complex plane is a circle.
Solution:
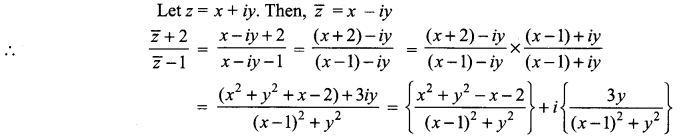
It is given that the real part of ![]() is 4.
is 4.
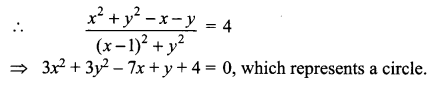
Question 3.

Solution:

![]()
Question 4.
If arg (z – 1) = \(\frac{\pi}{6}\) and arg (z + 1) = 2 \(\frac{\pi}{3}\) , then prove that |z| = 1.
Solution:
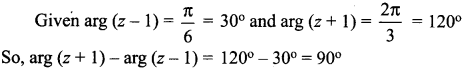

Question 5.
P represents the variable complex number z. Find the locus of P, if 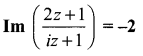
Solution:

Question 6.
P represents the variable complex number z. Find the locus of P, if 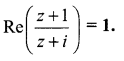
Solution:
Let z = x + iy