You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.3
Question 1.
Solve the cubic equation: 2x3 – x2 – 18x + 9 = 0 if sum of two of its roots vanishes.
Solution:
The given equation is 2x3 – x2 – 18x + 9 = 0
\(x^{3}-\frac{x^{2}}{2}-9 x+\frac{9}{2}=0\)
Let the roots be α, -α, β
α – α + β = \(-\left(\frac{-1}{2}\right)\)
\(\Rightarrow \beta=\frac{1}{2}\)
(α) (-α) (β) = \(\frac{-9}{2}\)
\(\Rightarrow-\alpha^{2}\left(\frac{1}{2}\right)=\frac{-9}{2}\)
α2 = 9
α = ±3
The roots are 3, -3, \(\frac { 1 }{ 2 }\)
Question 2.
Solve the equation 9x3 – 36x2 + 44x – 16 = 0 if the roots form an arithmetic progression.
Solution:
The given equation is 9x3 – 36x2 + 44x – 16 = 0
\(x^{3}-4 x^{2}+\frac{44}{9} x-\frac{16}{9}=0\)
Let the roots be α – d, α, α + d
As they are in A.P

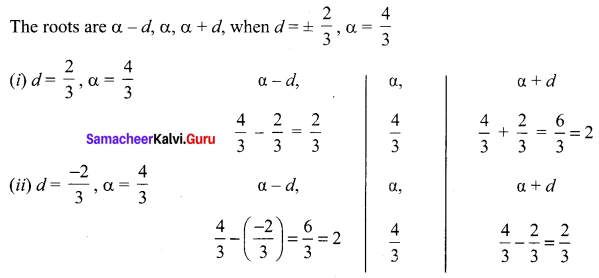
![]()
Question 3.
Solve the equation 3x3 – 26x2 + 52x – 24 = 0 if its roots form a geometric progression.
Solution:
The given equation is 3x3– 26x2 + 52x – 24 = 0
\(x^{3}-\frac{26}{3} x^{2}+\frac{52}{3} x-8=0\)
Given that the root are GP
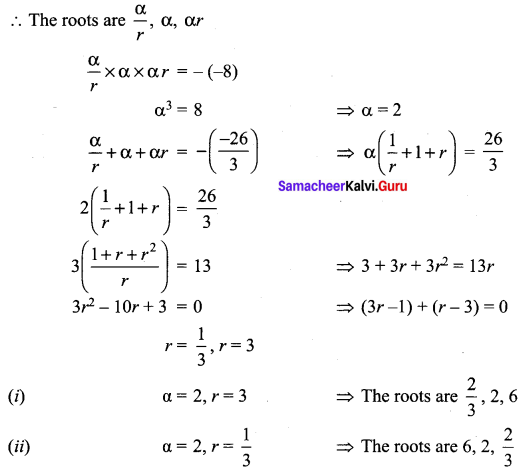
Question 4.
Determine ft and solve the equation 2x3 – 6x2 + 3x + k = 0 if one of its roots is twice the sum of the other two roots.
Solution:
The given equation is 2x3 – 6x2 + 3x + k = 0
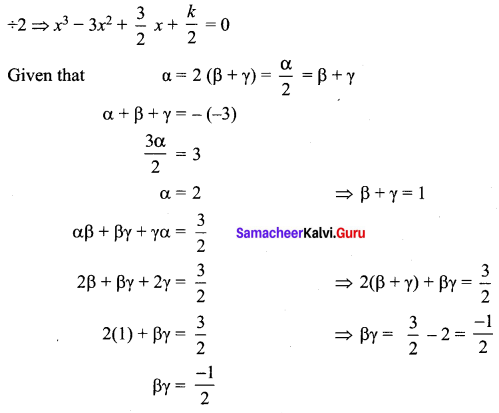
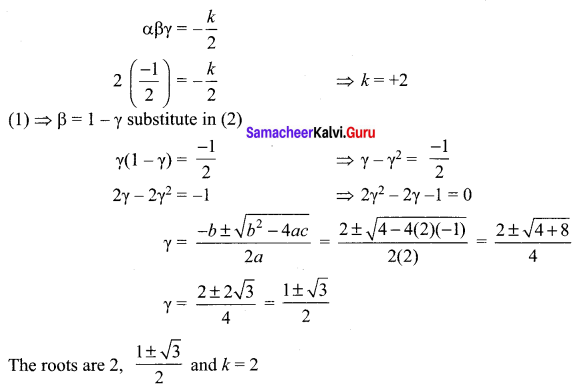
Question 5.
Find all zeros of the polynomial x6 – 3x5 – 5x4 + 22x3 – 39x2 – 39x + 135, if it is known that 1 + 2i and √3 are two of its zeros.
Solution:
The given equation is x6 – 3x5 – 5x4 + 22x3 – 39x2 – 39x + 135 = 0
The given roots are 1 + 2i, √3
The other roots are 1 – 2i, -√3
The factors are
= {x2 – x(2) + (1 + 4)}{(x + √3)(x – √3)}
= (x2 – 2x + 5) (x2 – 3)
= x4 – 3x2 – 2x3 + 6x + 5x2 – 15
= x4 – 2x3 + 2x2 + 6x – 15
To find this roots,

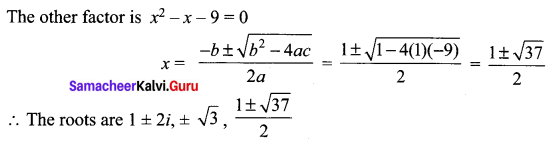
Question 6.
Solve the cubic equations:
(i) 2x3 – 9x2 + 10x = 3
(ii) 8x3 – 2x2 – 7x + 3 = 0
Solution:
(i) Given equation is 2x3 – 9x2 + 10x = 3
Sum of the co-efficients = 0
(x – 1) is a factor.
The other factor is 2x2 – 7x + 3
2x2 – 7x + 3 = 0
(x – 3)(2x – 1) = 0
The roots are 1, 3, \(\frac { 1 }{ 2 }\)
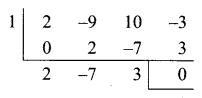
(ii) Given equation is 8x3 – 2x2 – 7x + 3 = 0
Sum of odd co-efficients = Sum of even co-efficients
(x + 1) is a factor.
The other factor is 8x2 – 10x + 3
8x2 – 10x + 3 = 0
(4x – 3) (2x – 1) = 0
The roots are \(\frac{3}{4}, \frac{1}{2},-1\)
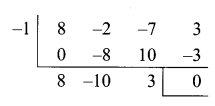
![]()
Question 7.
Solve the equation: x4 – 14x2 + 45 = 0.
Solution:
The given equation is x4 – 14x2 + 45 = 0
Let x2 = y
y2 – 14y + 45 = 0
(y – 9)(y – 5) = 0
y = 9, 5
x2 = 9, x2 = 5
x = ± 3, x = ± √5
The roots are ± 3, ± √5
Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.3 Additional Problems
Question 1.
If one root of x3 + 2x2 + 3x + k = 0 is sum of the other two roots then find the value of k.
Solution:
Let α, β, γ be the roots of given equation.
But, α = β + γ
α + β + γ = -2 … (1) ⇒ 2α = -2 ⇒ α = -1
αβ + βγ + γα = 3 … (2) This gives β + γ = – 1
αβγ = -k …(3)
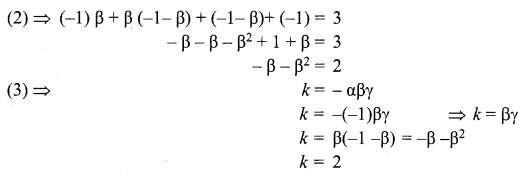
Question 2.
If sum of the roots of the equation x3 – 3x2 – 16x + k = 0 is zero then find the value of k.
Solution:
Let α, β, γ be the roots of given equation.
But, α + β = 0

Question 3.
Find all zeros of the polynomial x3 – 5x2 + 9x – 5 = 0, If 2 + i is a root.
Solution:
