Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.6

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.6

Question 1.
Discuss the maximum possible number of positive and negative roots of the polynomial equation 9x⁹ – 4x⁸ + 4x⁷ – 3x⁶ + 2x⁵ + x³ + 7x² + 7x + 2 = 0.
Solution:
P(x) = 9x⁹ – 4x⁸ + 4x⁷ – 3x⁶ + 2x⁵ + x³ + 7x² + 7x + 2
The number of sign changes in P(x) is 4.
∴P(x) has atmost 4 positive roots.
P(-x) = -9x⁹ – 4x⁸ – 4x⁷ – 3x⁶ – 2x⁵ – x³ + 7x² – 7x + 2
The number of sign changes in P(-x) is 3.
P(x) has almost 3 negative roots. Since the difference between the number of sign changes in co-efficient P(-x) and the number of negative roots of the polynomial P(x) is even.
The number of negative roots = at most 2.

Question 2.
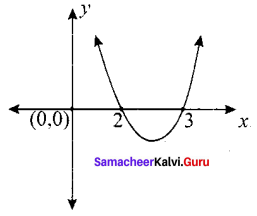
Discuss the maximum possible number of positive and negative zeros of the polynomials x² – 5x + 6 and x² – 5x + 16. Also, draw a rough sketch of the graphs.
Solution:
P(x) = x² – 5x + 6
The number of sign changes in P(x) is 2.
P(x) has atmost 2 positive roots. P(-x) = x² + 5x + 6.
The number of sign changes in P(-x) is 0.
∴ P (x) has no negative roots. P (x) = x² – 5x + 16

Question 3.
Show that the equation x⁹ – 5x⁵ + 4x⁴ + 2x² +1 = 0 has atleast 6 imaginary solutions.
Solution:
P(x) = x⁹ – 5x⁵ + 4x⁴ + 2x² + 1
(i) The number of sign changes in P(x) is 2. The number of positive roots is atmost 2.
(ii) P(-x) = -x⁹ + 5x⁵ + 4x⁴ + 2x² + 1. The number of sign changes in P(-x) is 1. The number of negative roots of P (x) is atmost 1. Since the difference of number of sign changes in P(-x) and number of negative zeros is even.
P(x) has one negative root.
(iii) 0 is not the zero of the polynomial P(x). So the number of real roots is almost 3.
∴ The number of imaginary roots at least 6.

Question 4.
Determine the number of positive and negative roots of the equation x⁹ – 5x⁸ – 14x⁷ = 0.
Solution:
x⁹ – 5x⁸ – 14x⁷ = 0
P (x) = x⁹ – 5x⁸ – 14x⁷. The number of sign changes is P(x) is 1.
The number of positive roots is 1. P (-x) = -x⁹ – 5x⁸ + 14x⁷
The number of sign changes is P(-x) is one. The number of negative zero of P(-x) is 1. It is clear that 0 is a root of the equation.
∴ The number of the imaginary roots is at least 6.

Question 5.
Find the exact number of real zeros and imaginary of the polynomial x⁹ + 9x⁷ + 7x⁵ + 5x³ + 3x.
Solution:
P(x) = x⁹ + 9x⁷ + 7x⁵ + 5x³ + 3x.
There is no change in the sign of P(x) and P(-x), P(x) has no positive and no negative real roots, but 0 is the root of the polynomial equation P(x).

Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.6 Additional Problems

Question 1.
Find the maximum possible number of real roots of the equation, x⁵ – 6.x² – 4x + 5 = 0.
Solution:
Let f(x) = x⁵ – 6x² – 4x + 5
Check the terms when it changes sign
Number of changes = 2
∴ Maximum number of positive real roots = 2
f(-x) = (- x)⁵ – 6 (- x)² – 4 (-x) + 5
= -x⁵ – 6x² + 4x + 5
Check the terms when it changes signs.
Number of changes = 1
∴ Maximum number of negative real roots = 1
∴ Total maximum number of real roots = 2 + 1 = 3

Question 2.
Find the number of real roots of the equation, x² + 5 |x| + 6 = 0.
Solution:
|x²| – 5|x| + 6 = 0
(|x| -2) (|x| -3) = 0

It has four real roots. The real roots are 2, -2, 3, -3

Question 3.
Find the real roots of the equation, x² + 5 |x| + 6 = 0.
Solution:
x² + 5 |x| + 6 = 0
Case (i) If x ≥ 0
x² + 5x + 6 = 0
(x + 2) (x + 3) = 0
x = -2 and x = -3
Case (ii) If x < 0
x² – 5x + 6 = 0
(x – 2) (x – 3) = 0
x = 2 and x = 3

Question 4.
Solve x⁴ – 4x² + 8x + 35 = 0. Given (2 + \(i \sqrt{3}\)) is a root.
Solution:

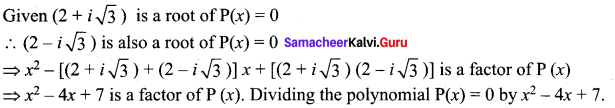
⇒ x² – 4x + 7 is a factor of P (x). Dividing the polynomial P(x) = 0 by x² – 4x + 7.
We get x² + 4x + 5 = 0 is a other factor. The roots of x² + 4x + 5 = 0 are

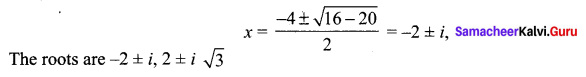
Question 5.
Solve x⁴ – 5x³ + 4x² + 8x – 8 = 0. Given (1 – \(\sqrt{5}\)) is a root of the polynomial equation.
Solution:
Since (1 – \(\sqrt{5}\)) is a root of the polynomial P(x) = 0
(1 + \(\sqrt{5}\)) is also a root of P (x) = 0
⇒ x² – [(1 + \(\sqrt{5}\)) + (1 – \(\sqrt{5}\))] x + (1 + \(\sqrt{5}\) ) (1 – \(\sqrt{5}\) ) = 0 is a factor of P(x) = 0 ⇒ x² – 2x – 4 = 0 is a factor of P(x) = 0.
Dividing the polynomial by x² – 2x – 4 = 0
We get the other factor x² – 3x + 2 = 0
The roots of x² – 3x + 2 = 0
(x – 2) (x – 1) = 0
x = 1, 2
The roots are 1, 2, 1 ± \(\sqrt{5}\)

Question 6.
Find a polynomial equation of the lowest degree with rational co-efficient having \(\sqrt{3}\), (1 – 2i) as two of its roots.
Solution:
When \(\sqrt{3}\) is a root, – \(\sqrt{3}\) will also be a root.
Now the quadratic equation with \(\sqrt{3}\) , – \(\sqrt{3}\) are roots is x² – (\(\sqrt{3}\) – \(\sqrt{3}\))x + (\(\sqrt{3}\))(-\(\sqrt{3}\)) = 0
(i.e) x² – 3 = 0
When 1 – 2i is a root, 1 + 2i will be another root.
Now the quadratic equation with roots 1 – 2i and 1 + 2i is
x² – (1 – 2i + 1 + 2i)x + (1 – 2i)(1 + 2i) = 0
(i.e) x² – 2x + 5 = 0
∴ The equation with roots ± \(\sqrt{3}\) and 1 ± 2i is (x² – 3) (x² – 2x + 5) = 0
(i.e) x⁴ – 2x³ + 5x² – 3x² + 6x – 15 = 0 ,
(i.e) x⁴ – 2x³ + 2x² + 6x – 15 = 0