You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.7
Choose the correct or the most suitable answer from the given four alternatives:
Question 1.
A zero of x3 + 64 is _______
(a) 0
(b) 4
(c) 4i
(d) -4
Answer:
(d) -4
Hint: x3 + 64 = 0
⇒ x3 = -64
⇒ x3 = (-4)3
⇒ x = -4
Question 2.
If f and g are polynomials of degrees m and n respectively, and if h(x) = (f 0 g) (x), then the degree of h is ______
(a) mn
(b) m + n
(c) mn
(d) nm
Answer:
(a) mn
![]()
Question 3.
A polynomial equation in x of degree n always has _______
(a) n distinct roots
(b) n real roots
(c) n imaginary roots
(d) at most one root.
Answer:
(c) n imaginary roots (Every real number is also imaginary)
Question 4.
If α, β and γ are the zeros of x3 + px2 + qx + r, then \(\sum \frac{1}{\alpha}\) is ______
(a) \(-\frac{q}{r}\)
(b) \(\frac{q}{p}\)
(c) \(\frac{q}{r}\)
(d) \(-\frac{q}{p}\)
Answer:
(a) \(-\frac{q}{r}\)
Hint:
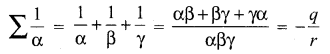
Question 5.
According to the rational root theorem, which number is not possible rational zero of 4x7 + 2x4 – 10x3 – 5?
(a) -1
(b) \(\frac{5}{4}\)
(c) \(\frac{4}{5}\)
(d) 5
Answer:
(c) \(\frac{4}{5}\)
Hint:
an = 4; a0 = 5
Let \(\frac{p}{q}\) be the root of P (x). P must divide 5, possible values of P are ±1, ±5
q must divide 4, possible values of q are ±1, ±2, ±4
Possible roots are \(\pm 1, \pm \frac{1}{2}, \pm \frac{1}{4}, \pm 5, \pm \frac{5}{2}, \pm \frac{5}{4}\)
Question 6.
The polynomial x3 – kx2 + 9x has three real zeros if and only if, k satisfies.
(a) |k| ≤ 6
(b) k = 0
(c) |k| > 6
(d) |k| ≥ 6
Answer:
(d) |k| ≥ 6
Hint:
x3 – kx2 + 9x = 0
⇒ x (x2 – kx + 9) = 0
x = 0 is one real root. If the remaining roots to be real if the
b2 – 4ac ≥ 0
⇒ k2 – 36 ≥ 0
⇒ k2 ≥ 36
⇒ |k| ≥ 6
![]()
Question 7.
The number of real numbers in [0, 2π] satisfying sin4 x – 2sin2 x + 1 is ______
(a) 2
(b) 4
(c) 1
(d) ∞
Answer:
(c) 1
Hint:
sin4 x – 2sin2 x + 1 = 0
⇒ t2 – 2t + 1 = 0
⇒ (t – 1)2 = 0
⇒ t – 1 = 0
⇒ t = 1
⇒ sin2 x = 1
⇒ \(\frac{1-\cos 2 x}{2}=1\)
⇒ 1 – cos 2x = 2
⇒ cos 2x = cos 0
⇒ 2x = 2nπ
⇒ x = nπ
n = 0, x = 0
n = 1, x = π
n = 2, x = 2π
![]()
Question 8.
If x3 + 12x2 + 10ax + 1999 definitely has a positive zero, if and only if _______
(a) a ≥ 0
(b) a > 0
(c) a < 0
(d) a ≤ 0
Answer:
(c) a < 0
Hint:
If a < 0, then P(x) = x3 + 12x2 + 10ax + 1999 has 2 changes of sign.
∴ P (x) has atmost two positive roots. So a < 0
Question 9.
The polynomial x3 + 2x + 3 has _______
(a) one negative and two imaginary zeros
(b) one positive and two imaginary zeros
(c) three real zeros
(d) no zeros
Answer:
(a) one negative and two imaginary zeros
Hint:
P(x) = x3 + 2x + 3; No positive root.
P(-x) = -x3 – 2x + 3; Only one change in the sign.
∴ One negative root.
Question 10.
The number of positive zeros of the polynomial 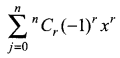 is ______
is ______
(a) 0
(b) n
(c) <n
(d) r
Answer:
(b) n