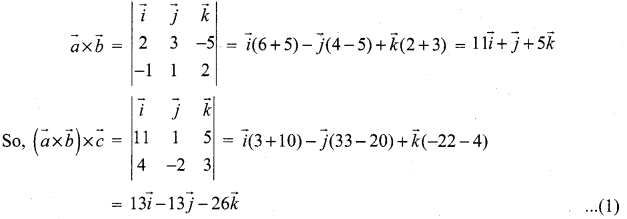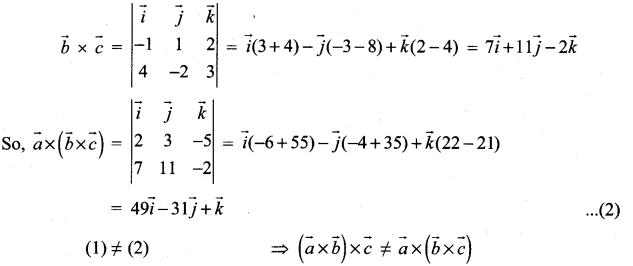You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.2
Question 1.
![]()
Solution:

Question 2.
Find the volume of the parallelepiped whose coterminous edges are represented by the vectors ![]() .
.
Solution:
Volume of the parallelepiped = \(\| \vec{a}, \vec{b}, \vec{c}]\)
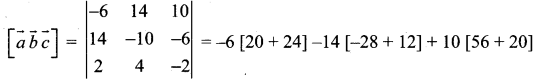
= -264 + 224 + 760 = 720 cubic units
![]()
Question 3.
The volume of the parallelepiped whose coterminus edges are ![]() , \(-3 \vec{i}+7 \vec{j}+5 \vec{k}\) is 90 cubic units. Find the value of λ
, \(-3 \vec{i}+7 \vec{j}+5 \vec{k}\) is 90 cubic units. Find the value of λ
Solution:
Given, Volume of the parallelepiped = 90 cubic units

Question 4.
If \(\vec{a}, \vec{b}, \vec{c}\) are three non-coplanar vectors represented by concurrent edges of a parallelepiped of volume 4 cubic units, find the value of ![]()
Solution:
Let \(\vec{a}, \vec{b}, \vec{c}\) be the concurrent edges of parallelepiped
Given volume of parallelepiped = 4 cubic units

Question 5.
Find the altitude of a parallelepiped determined by the vectors \(\vec{a}=-2 \hat{i}+5 \hat{j}+3 \hat{k}\), \(\hat{b}=\hat{i}+3 \hat{j}-2 \hat{k}\) and \(\vec{c}=-3 \vec{i}+\vec{j}+4 \vec{k}\) if the base is taken as the parallelogram determined by b and c.
Solution:
Volume = Base Area × Height
\(|[\vec{a}, \vec{b}, \vec{c}]|=|\vec{b} \times \vec{c}|\) × Height

![]()
Question 6.
Determine whether the three vectors \(2 \hat{i}+3 \hat{j}+\hat{k}, \hat{i}-2 \hat{j}+2 \hat{k}\) and \(3 \hat{i}+\hat{j}+3 \hat{k}\) are coplanar.
Solution:
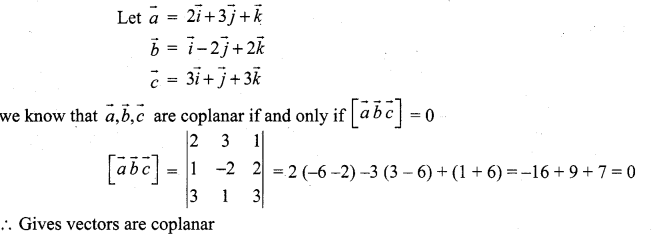
Question 7.
Let ![]() If c1 = 1 and c2 = 2, find c3 such that \(\vec{a}, \vec{b}\) and \(\vec{c}\) and c are coplanar.
If c1 = 1 and c2 = 2, find c3 such that \(\vec{a}, \vec{b}\) and \(\vec{c}\) and c are coplanar.
Solution:

Question 8.
If ![]() , show that \([\vec{a} \vec{b} \vec{c}]\) depends neither x nor y.
, show that \([\vec{a} \vec{b} \vec{c}]\) depends neither x nor y.
Solution:
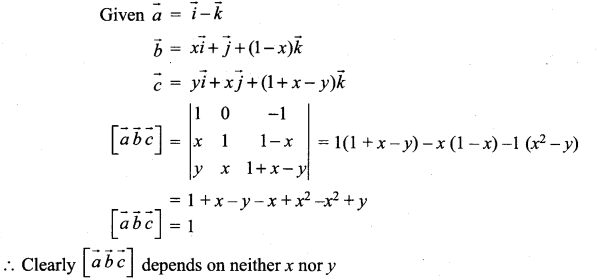
Question 9.
If the vectors
![]()
are coplanar, prove that c is the geometric mean of a and b.
Solution:

∴ c is the geometric means of ‘a’ and ‘b’.
Question 10.
Let \(\vec{a}, \vec{b}, \vec{c}\) be three non-zero vectors such that \(\vec{c}\) is a unit vector perpendicular to both \(\vec{a}\) and \(\vec{b}\). If the angle between \(\vec{a}\) and \(\vec{b}\) is \(\frac{\pi}{6}\) show that ![]() .
.
Solution:
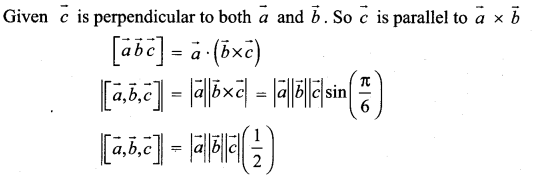

Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.2 Additional Problems
Question 1.
If the edges ![]() meet a vertex, find the volume of the parallelepiped.
meet a vertex, find the volume of the parallelepiped.
Solution:
Volume of the parallelepiped = 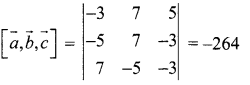
The volume cannot be negative
∴ Volume of parallelepiped = 264 cu. units
Question 2.
If ![]() and \(\vec{x} \neq \overrightarrow{0}\) then show that \(\vec{a}, \vec{b}, \vec{c}\) are coplanar.
and \(\vec{x} \neq \overrightarrow{0}\) then show that \(\vec{a}, \vec{b}, \vec{c}\) are coplanar.
Solution:

![]()
Question 3.
The volume of a parallelepiped whose edges are represented by \(-12 \vec{i}+\lambda k\), \(3 \vec{j}-\vec{k}, 2 \vec{i}+\vec{j}-15 \vec{k}\) is 546. Find the value of λ.
Solution:
Volume of the parallelepiped = 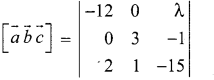
= -12 [-45 + 1] – 0 () + λ [0 – 6] = -12 (-44) -6 λ
= 528 – 6λ = 546 (given)
⇒ -6λ = 546 – 528 = 18
∴ λ = \(\frac{18}{-6}\) = -3
Question 4.
Prove that \(|\vec{a} \vec{b} \vec{c}|\) = abc if and only if \(\vec{a}, \vec{b}, \vec{c}\) are mutually perpendicular.
Solution:
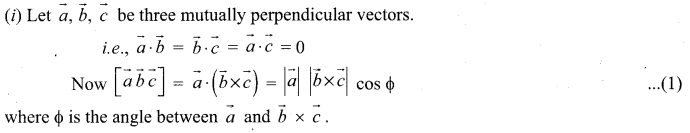
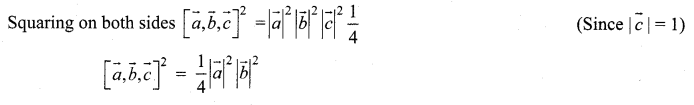
Question 5.
Show that the points (1, 3, 1), (1, 1, -1), (-1, 1, 1), (2, 2, -1) are lying on the same plane.
Solution:

Question 6.
![]()
Solution: