You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.5
Question 1.
Find the parametric form of vector equation and Cartesian equations of a straight line passing through (5, 2, 8) and is perpendicular to the straight lines
![]()
Solution:
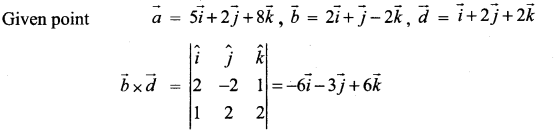
∴ This’ vector is perpendicular to both the given straight lines.
∴ The required straight line is
\(\vec{r}=\vec{a}+t(\vec{b} \times \vec{d})\)
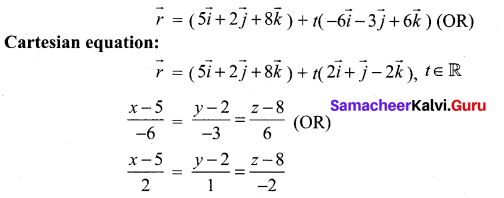
Question 2.
Show that the lines ![]() are skew lines and hence find the shortest distance between them.
are skew lines and hence find the shortest distance between them.
Solution:

![]()
Question 3.
If the two lines ![]() intersect at a point, find the value of m.
intersect at a point, find the value of m.
Solution:

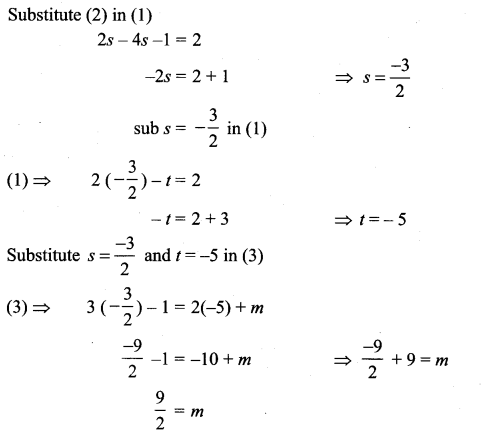
Question 4.
Show that the lines \(\frac{x-3}{3}=\frac{y-3}{-1}\), z – 1 = 0 and \(\frac{x-6}{2}=\frac{z-1}{3}\), y – 2 = 0 intersect. Also find the point of intersection
Solution:

Any point on the Second line
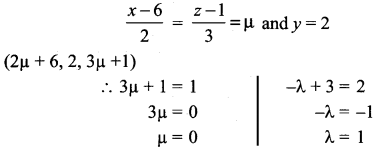
∴ The required point of intersection is (6, 2, 1)
Question 5.
Show that the straight lines x + 1 = 2y = -12z and x = y + 2 = 6z – 6 are skew and hence find the shortest distance between them.
Solution:
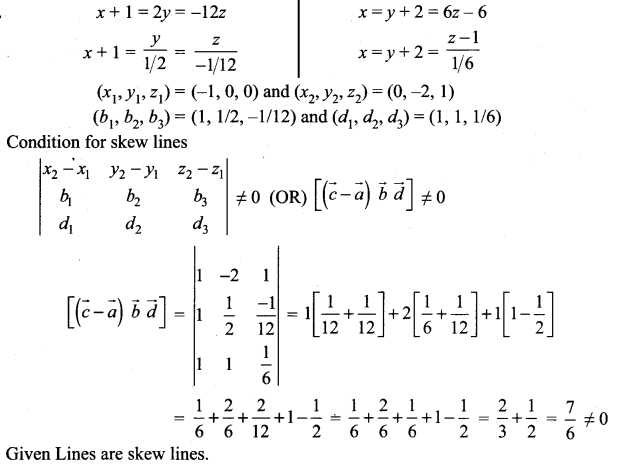

Question 6.
Find the parametric form of vector equation of the straight line passing through (-1, 2, 1) and parallel to the straight line \(\vec{r}=(2 \hat{i}+3 \hat{j}-\hat{k})+t(\hat{i}-2 \hat{j}+\hat{k})\) and hence find the shortest distance between the lines.
Solution:

![]()
Question 7.
Find the foot of the perpendicular drawn from the point (5, 4, 2) to the line \(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}\). Also, find the equation of the perpendicular.
Solution:

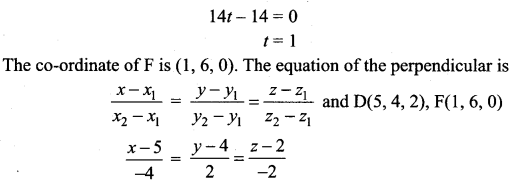
Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.5 Additional Problems
Question 1.
Find the shortest distance between the parallel line
![]()
Solution:
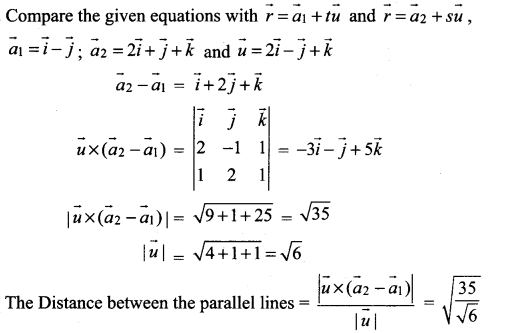
Question 2.
Show that the two lines \(\vec{r}=(\vec{i}-\vec{j})+t(2 \vec{i}+\vec{k})\) and \(\vec{r}=(2 \vec{i}-\vec{j})+s(\vec{i}+\vec{j}-\vec{k})\) skew lines and find the distance between them.
Solution:
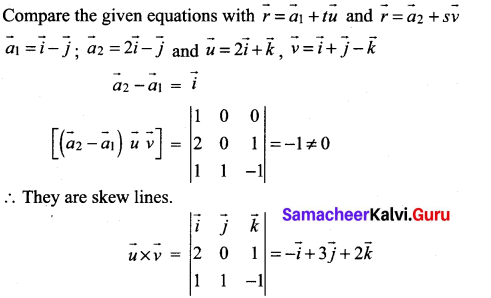

Question 3.
Show that the lines 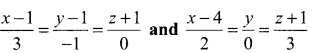 intersect and hence find the point of intersection
intersect and hence find the point of intersection
Solution:

Any point on this line is of the form (2µ + 4, 0, 3µ – 1)
Since they are intersecting, for some λ, µ
(3λ + 1, – λ + 1,- 1) = (2µ + 4, 0, 3µ – 1) ⇒ λ = 1 and µ = 0
To find the point of intersection either take λ = 1 or µ = 0
∴ The point of intersection is (4, 0, – 1),
![]()
Question 4.
Find the shortest distance between the skew lines.
![]()
Solution:
Compare the given equation with \(\vec{r}=\vec{a}_{1}+t \vec{u}\) and \(\vec{r}=\vec{a}_{2}+s \vec{v}\)
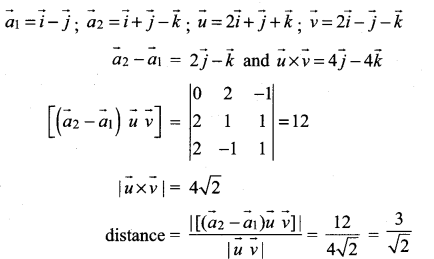
Question 5.
Find the shortest distance between the parallel lines.
![]()
Solution:
