Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.7

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.7

Question 1.
Find the non-parametric form of vector equation, and Cartesian equation of the plane passing through the point (2, 3, 6) and parallel to the straight lines \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-3}{1}\) and \(\frac{x+3}{2}=\frac{y-3}{-5}=\frac{z+1}{-3}\)
Solution:

Question 2.
Find the parametric form of vector equation, and Cartesian equations of the plane passing through the points (2, 2, 1), (9, 3, 6) and perpendicular to the plane 2x + 6y + 6z = 9.
Solution:
The required plane passes through the points

Question 3.
Find the parametric form of vector equation and Cartesian equations of the plane passing through the points (2, 2, 1), (1, -2, 3) and parallel to the straight line passing through the points (2, 1, -3) and (-1, 5, -8).
Solution:
Equation of the straight line passing through the points (2, 1, -3) and (-1, 5, -8) is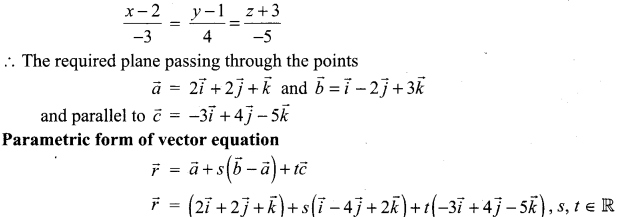

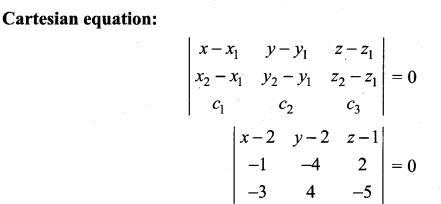
(x – 2) [20 – 8] – (y – 2) [5 + 6] + (z – 1) [-4 – 12] = 0
12(x – 2) – 11(y – 2) – 16(z – 1) = 0
12x – 24 – 11y + 22 – 16z + 16 = 0
12x – 11y – 16z + 14 = 0

Question 4.
Find the non-parametric form of vector equation of the plane passing through the point (1, -2, 4) and perpendicular to the plane x + 2y – 3z = 11 and parallel to the line \(\frac{x+7}{3}=\frac{y+3}{-1}=\frac{z}{1}\)
Solution:
The required plane passing through the point \(\vec{a}=\vec{i}-2 \vec{j}+4 \vec{k}\) and parallel to the plane \(\vec{b}=\vec{i}+2 \vec{j}-3 \vec{k}\) and parallel to the line \(\vec{c}=3 \vec{i}-\vec{j}+\vec{k}\)

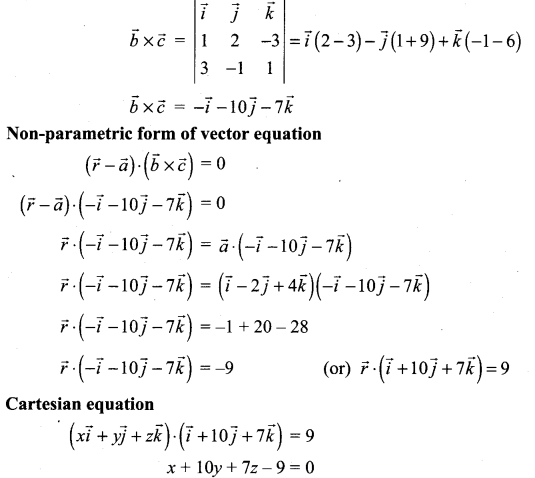
Question 5.
Find the parametric form of vector equation, and Cartesian equations of the plane containing the line \(\vec{r}=(\hat{i}-\hat{j}+3 \hat{k})+t(2 \hat{i}-\hat{j}+4 \hat{k})\) and perpendicular to the plane \(\vec{r} \cdot(\hat{i}+2 \hat{j}+\hat{k})\) = 8.
Solution:
The required plane passing through the point \(\vec{a}=\vec{i}-\vec{j}+3 \vec{k}\) and parallel to \(\vec{b}=2 \vec{i}-\vec{j}+4 \vec{k}\) and \(\vec{c}=\vec{i}+2 \vec{j}+\vec{k}\)
Parametric form of vector equation

(x – 1) [-1 – 8] – (y + 1)[z – 4] + (z – 3) [4 + 1] = 0
-9(x- 1) + 2(y + 1) + 5(z- 3) = 0
-9x + 9 + 2y + 2 + 5z – 15 = 0
-9x + 2y + 5z – 4 = 0
9x – 2y – 5z + 4 = 0

Question 6.
Find the parametric vector, non-parametric vector and Cartesian form of the equation of the plane passing through the point (3, 6, -2), (-1, -2, 6) and (6, 4, -2).
Solution:
The required plane passing through the points

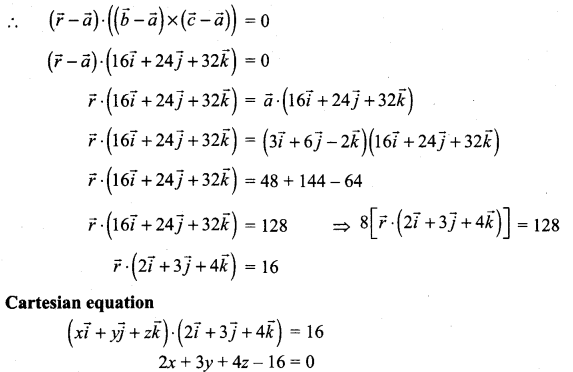
Question 7.
Find the non-parametric form of vector equation, and Cartesian equations of the plane

Solution:

Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.7 Additional Problem

Question 1.
Find the vector and cartesian equations of the plane containing the line \(\frac{x-2}{2}=\frac{y-2}{3}=\frac{z-1}{3}\) and parallel to the line \(\frac{x+1}{3}=\frac{y-1}{2}=\frac{z+1}{1}\)
Solution:
The required plane passes through the point A(2, 2, 1) and parallel to

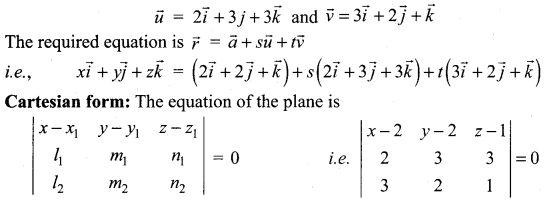
i.e., (x – 2)[3 – 6] – (y – 2)[2 – 9] + (z – 1)[4 – 9] = 0
i.e., (x – 2)(-3) + (y – 2)(7) – 5(z – 1) = 0
-3x + 6 + 7y – 14 – 5z + 5 = 0
-3x + 7y – 5z – 3 = 0 i.e. 3x – 7y + 5z + 3 = 0

Question 2.
Find the vector and cartesian equation of the plane passing through the point (1, 3, 2) and parallel to the lines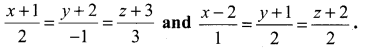
Solution:
The required plane passes through the point A = (1, 3, 2) and parallel to the vectors

i.e. (x – 1)(-2 – 6) – (y – 3)(4 – 3) + (z – 2)(4 + 1) = 0
—8(x – 1) – 1(y – 3) + 5(z – 2) = 0
-8x + 8 – y + 3 + 5z – 10 = 0
-8x – y + 5z + 1 = 0 i.e. 8x + y – 5z – 1 = 0

Question 3.
Find the vector and cartesian equations of the plane passing through the point (-1, 3, 2) and perpendicular to the planes x + 2y + 2z = 5 and 3x + y + 2z = 8
Solution:
The normal vector to the given planes x + 2y + 2z = 5 and 3x + y + 2z = 8 are respectively \(\vec{i}+2 \vec{j}+2 \vec{k}\) and \(3 \vec{i}+\vec{j}+2 \vec{k}\). These vectors are parallel to the required plane
The required plane passes through the point A(-1, 3, 2) and parallel to the vectors

i.e., (x + 1)(4 – 2) – (y – 3)(2 – 6) + (z – 2)(1 – 6) = 0
2(x + 1) + 4(y – 3) – 5(z – 2) = 0
2x + 2 + 4y – 12 – 5z + 10 = 0
2x + 4y – 5z = 0

Question 4.
Find the vector and cartesian equations of the plane passing through the points A(1, -2, 3) and B(-1, 2, -1) and is parallel to the line \(\frac{x-2}{2}=\frac{y+1}{3}=\frac{z-1}{4}\)
Solution:
The vector equation of the plane is

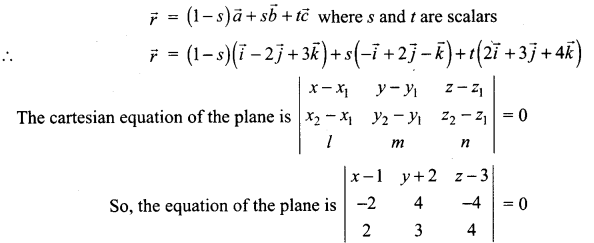
i.e, (x – 1)[16 + 12] – (y + 2)(-8 + 8) + (z – 3)(-6 – 8) = 0
28(x – 1) – 14(z – 3) = 0
28x – 28 – 14z + 42 = 0
28x – 14z + 14 = 0
(÷ by 14) ⇒ 2x – z + 1 = 0

Question 5.
Find the vector and cartesian equations of the plane through the points (1, 2, 3) and (2,3,1) and perpendicular to the plane 3x – 2y + 4z – 5 = 0.
Solution:
The vector normal to the plane 3x – 2y + 4z – 5 = 0 is \(3 \vec{i}-2 \vec{j}+4 \vec{k}\)
The required plane is parallel to the vector \(3 \vec{i}-2 \vec{j}+4 \vec{k}\)
∴ Vector equation of the plane passing through two points and parallel to one vector is

i.e. (x – 1)[4 – 4] – (y – 2)[4 + 6] + (z – 3)[-2 – 3] = 0
-10(y – 2) – 5(z – 3) = 0
-10y + 20 – 5z + 15 = 0
-10y – 5z + 35 = 0
10y + 5z – 35 = 0
(÷ by 5) ⇒ 2y + z – 1 = 0

Question 6.
Find the vector and cartesian equations of the plane containing the line \(\frac{x-2}{2}=\frac{y-2}{3}=\frac{z-1}{-2}\) and passing through the point (-1, 1, -1).
Solution:
The required plane passes through the points A(-1, 1,-1) and B(2, 2, 1) and parallel to the vectors \(\vec{c}=2 \vec{i}+3 \vec{j}-2 \vec{k}\) .
The required equation is

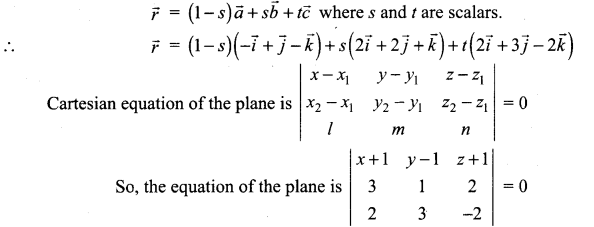
i.e. (x + 1)[-2 – 6] – (y – 1)[-6 – 4] + (z + 1)[9 – 2] = 0
-8(x + 1) + 10(y – 1) + 7(z + 1) = 0
-8x – 8 + 10y – 10 + 7z + 7 = 0
-8x + 10y + 7z – 11 = 0
i.e., 8x – 10y – 7z + 11 = 0

Question 7.
Find the vector and cartesian equations of the plane passing through the points with position vectors .
Solution:
Vector equation of the plane passing through three given non-collinear points is

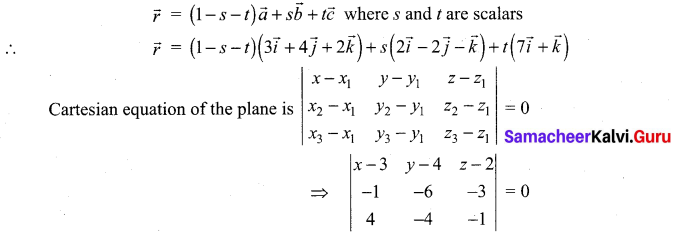
i.e. (x – 3)[6 – 12] – (y – 4)[1 + 12] + (z – 2)[4 + 24] = 0
-6(x – 3) – 13(y – 4) + 28(z – 2) = 0
-6x + 18 – 13y + 52 + 28z – 56 = 0
-6x – 13y + 28z + 14 = 0 .
i.e. 6x + 13y – 28z – 14 = 0

Question 8.
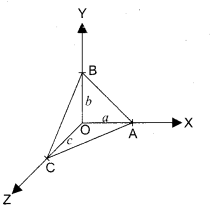
Derive the equation of the plane in the intercept form.
Solution:
Let the required plane makes intercepts on X, Y, Z-axes respectively as a, b and c.
i.e. A = (a, 0, 0)
B = (0, b, 0)
C = (0, 0, c)
The equation of the plane passing through three non-collinear points A, B and C is

Question 9.
Find the cartesian form of the following plane:

Solution:

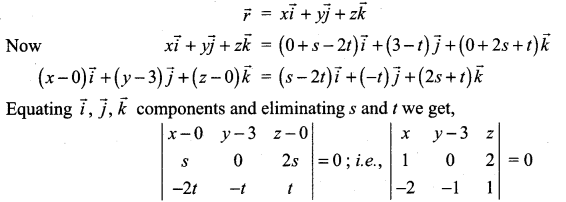
x(0 + 2) – (y – 3) (1 + 4) + z(-1) = 0
2x – 5(y – 3) – z = 0
2x – 5y + 15 – z = 0
2x – 5y – z + 15 = 0
which is the cartesian equation of the plane.