Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.8

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.8

Question 1.
Show that the straight lines and are coplanar. Find the vector equation of the plane in which they lie.
Solution:

Question 2.
Show that lines are coplanar. Also, find the plane containing these lines.
Solution:
From the lines we have,
(x₁, y₁, z₁) = (2, 3, 4) and (x₂, y₂, z₂) = (1, 4, 5)
(b₁, b₂, b₃) = (1, 1, 3) and (d₁, d₂, d₃) = (-3, 2, 1)
Condition for coplanarity

(x – 2)[1 – 6] – (y – 3)[1 + 9] + (z – 4)[2 + 3] = 0
-5(x – 2) – 10(y – 3) + 5(z – 4) = 0
-5x + 10 – 10y + 30 + 5z – 20 = 0
-5x – 10y + 5z + 20 = 0
(÷ by -5) ⇒ x + 2y – 2z – 4 = 0

Question 3.
If the straight lines are coplanar, find the district real values of m.
Solution:
From the lines we have,
(x₁, y₁, z₁) = (1, 2, 3) and (x₂, y₂, z₂) = (3, 2, 1)
(b₁, b₂, b₃) = (1, 2, m²) and (d₁, d₂, d₃) = (1, m², 2)
Condition for coplanarity
\(\left|\begin{array}{ccc}{x_{2}-x_{1}} & {y_{2}-y_{1}} & {z_{2}-z_{1}} \\ {b_{1}} & {b_{2}} & {b_{3}} \\ {d_{1}} & {d_{2}} & {d_{3}}\end{array}\right|=0\)

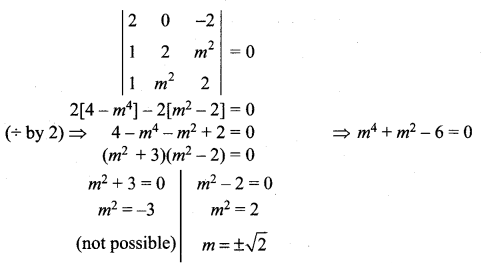
Question 4.
If the straight lines are coplanar, find λ and equation of the planes containing these two lines.
Solution:
From the lines we have,
(x₁, y₁, z₁) = (1, -1, 0) and (x₂, y₂, z₂) = (-1, -1, 0)
(b₁, b₂, b₃) = (2, λ, 2) and (d₁, d₂, d₃) = (5, 2, λ)
Condition for coplanarity

\(\left|\begin{array}{ccc}{x-1} & {y+1} & {z} \\ {2} & {-2} & {2} \\ {5} & {2} & {-2}\end{array}\right|\) = 0
(x – 1)[0] – (y + 1)[-4 – 10] + z[4 + 10] = 0
14(y + 1) + 14z = 0 ⇒ 14y + 14 + 14z = 0
(÷ by 14) ⇒ y + z + 1 = 0

Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.8 Additional Problems

Question 1.
Show that the straight lines.

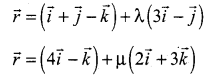
are coplanar. Find the vector equation of the plane in which they lie.
Solution:

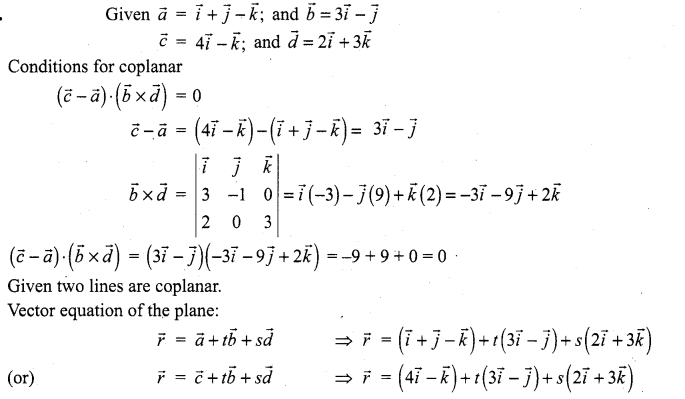
Question 2.
If the straight lines 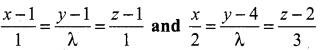are coplanar. Find λ.
Solution:
From the lines we have,
(x₁, y₁, z₁) = (1, 1, 1) and (b₁, b₂, b₃) = (1, λ, 1)
(x₂, y₂, z₂) = (0, 4, 2) and (d₁, d₂, d₃) = (2, λ, 3)
Condition for coplanarity
\(\left|\begin{array}{ccc}{x_{2}-x_{1}} & {y_{2}-y_{1}} & {z_{2}-z_{1}} \\ {b_{1}} & {b_{2}} & {b_{3}} \\ {d_{1}} & {d_{2}} & {d_{3}}\end{array}\right|\) = 0
\(\left|\begin{array}{ccc}{-1} & {3} & {1} \\ {1} & {\lambda} & {1} \\ {2} & {\lambda} & {3}\end{array}\right|\) = 0
-1(3λ – λ) – 3(3 – 2) + 1(λ – 2λ) = 0 ⇒ -2λ – 3 – λ = 0
-3λ = 3 ⇒ λ = -1

Question 3.
If the lines are coplanar, then find the value of k.
Solution:
From the lines we have,
(x₁, y₁, z₁) = (2, 3, 4) and (b₁, b₂, b₃) = (1, 1, -1)
(x₂, y₂, z₂) = (1, 4, 5) and (d₁, d₂, d₃) = (k, 2, 1)
Condition for coplanarity

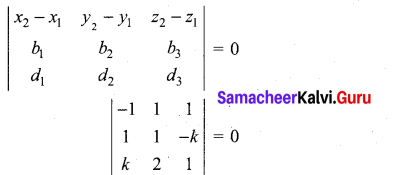
-1(1 + 2k) – 1(1 + k²) + 1(2 – k) = 0
-1 – 2k – 1 – k² + 2 – k = 0
-k² – 3k = 0
k² + 3k = 0
k(k + 3) = 0
k = 0 or k = -3

Question 4.
Show that the lines are coplanar, Also find the equation of the plane containing these two lines.
Solution:
From the lines we have,
(x₁, y₁, z₁) = (-3, 1, 5) and (b₁, b₂, b₃) = (-3, 1, 5)
(x₂, y₂, z₂) = (-1, 2, 5) and (d₁, d₂, d₃) = (-1, 2, 5)
Condition for coplanarity

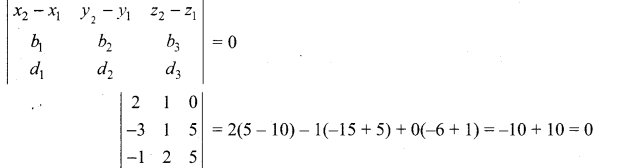
Given two lines are coplanar

(x + 3)[5 – 10] – (y – 1)[-15 + 5] + (z – 5)[-6 + 1] = 0
5(x + 3) + 10(y – 1) – 5(z – 5) = 0
(÷ by 5) ⇒ (x + 3) -2(y – 1) + (z – 5) = 0
x + 3 – 2y + 2 + z – 5 = 0
x – 2y + z = 0
or

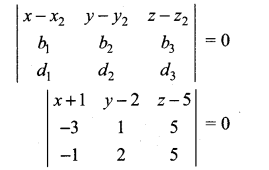
(x + 1)(5 – 10) – (y – 2)(-15 + 5) + (z – 5)(-6 + 1) = 0
-5(x + 1) + 10(y – 2) – 5(z – 5) = 0
(x + 1) – 2(y – 2) + (z – 5) = 0
x + 1 – 2y + 4 + z – 5 = 0
x – 2y + z = 0