You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.2
Question 1.
Find the slope of the tangent to the curves at the respective given points.
(i) y = x4 + 2x2 – x at x = 1
(ii) x = a cos3 t, sin 3 t at t = \(\frac{\pi}{2}\)
Solution:
(i) y = x4 + 2x2 – x at x = 1

Question 2.
Find the point on the curve y = x2 – 5x + 4 at which the tangent is parallel to the line 3x + y = 7.
Solution:
Let (x1, y1) be the required point.

Given tangent is similarly to the line ⇒ m1 = m2
⇒ 2x1 – 5 = -3
⇒ 2x1 = -3 + 5 = 2
⇒ x1 = 1
Substituting x1 = 1 in the curve.
y1 = 1 – 5 + 4 = 0
So the required point is (1, 0)
![]()
Question 3.
Find the points on the curves = x3 – 6x2 + x + 3 where the normal is parallel to the line x + y = 1729.
Solution:
Let (x1,y1) be the required point
y = x3 – 6x2 + x + 3

Substituting x1 values in the curve
when x1 = 4, y1 = 3
when x1 = 4, y1 = 43 – 6(4)2 + 4 + 3 = 64 – 96 + 4 + 3 = -25
So the required points are (0, 3) and (4, -25)
Question 4.
Find the points on the curve y2 – 4xy = x2 + 5 for which the tangent is horizontal.
Solution:
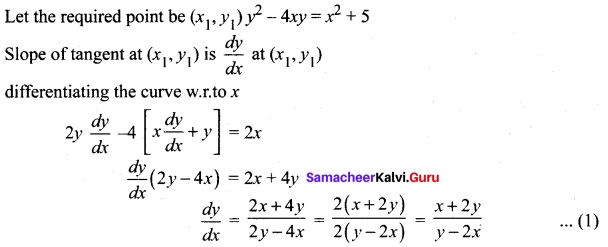
Given that tangent is horizontal (i.e) tangent is parallel to x – axis
⇒ Equation of tangent will be of the form y = c
![]()
from (1) and (2) we get
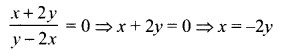
Substituting x = -2y in the equation of the curve we get
y2 – 4(-2y)(y) = 4y2 + 5
⇒ y2 + 8y2 – 4y2 = 5
⇒ 5y2 = 5 ⇒ y2 = 1
⇒ y = ± 1
when y = 1, x = -2 and when y = -1, x = 2 So the points are (2, -1), (-2, 1)
Question 5.
Find the tangent and normal to the following curves at the given points on the curve.
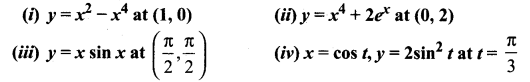
Solution:
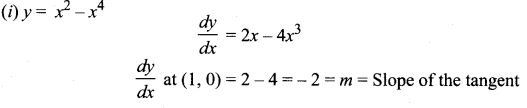
Now m = -2, (x1, y1) = (1, 0)
So equation of the tangent is
y – y1 = m(x – x1)
(i. e) y – 0 = -2(x – 1)
y = -2x + 2
2x+ y = 2
Slope of tangent = m = -2

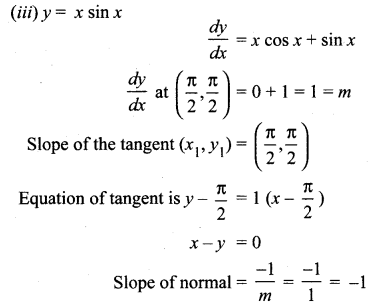

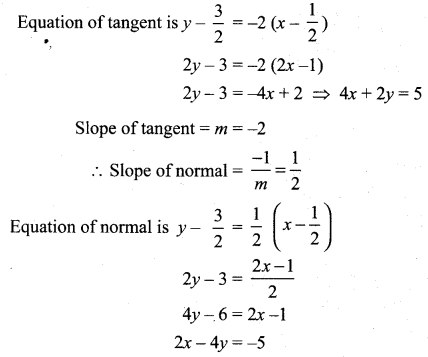
![]()
Question 6.
Find the equations of the tangents to the curve y = 1 + x3 for which the tangent is orthogonal with the line x + 12y = 12.
Solution:
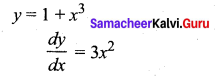
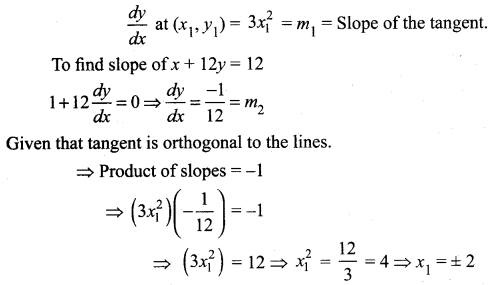
Substituting x1 values in the curve
when x1 = 2, y1 = 9; when x1 = -2, y1 = -1
So the points are (2, 9) and (-2, -7)
To find the equations of tangents:
Tangents are orthogonal to x + 12y = 12
So equations of tangents will be of the form 12x – y = k
The tangent passes through (2, 9) ⇒ 24 – 9 = k ⇒ k = 15 .
∴ Equation of tangent is 12x – y = 15
The tangent passes through (-2, -7) ⇒ 12 (-2) + 7 = k ⇒ -17
So equation of tangent is 12x – y = -17
Question 7.
Find the equations of the tangents to the curve y = \(\frac{x+1}{x-1}\)which are parallel to the line x + 2y = 6.
Solution:
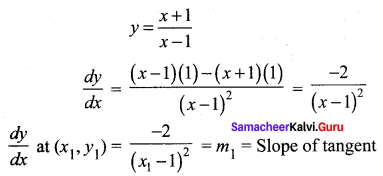
Tangent is parallel the line x + 2y = 6
⇒ Slope of tangent = Slope of line
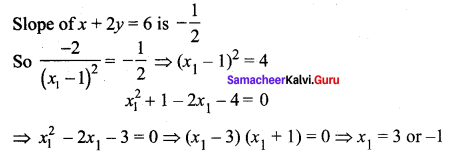
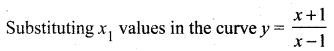
when x1 = -1, y1 = 0; when x1 = 3, y1 = 2
So the points are (-1, 0) and (3, 2). The tangents are parallel to x + 2y = 6. So equation of tangents will be of the form x + 2y = k.
∴ Equation of tangent is x + 2y = -1
The tangent passes through (-1, 0) ⇒ -1 = k
The tangent passes through (3, 2) ⇒ 3 + 4 = k ⇒ k = 7
∴ Equation of tangent is x + 2y = 7
Question 8.
Find the equation of tangent and normal to the curve given by x = 7 cos t and y = 2sin t, t ∈ R at any point on the curve.
Solution:

(2 cos t)y – 4 sint cos t = (7 sin t)x – 49 sin t cos t
x(7 sin t) – y(2 cos t) = 45 sin t cos t
Question 9.
Find the angle between the rectangular hyperbola xy = 2 and the parabola x2 + 4y = 0.
Solution:
Solving the given two equations. To find the point of intersection:
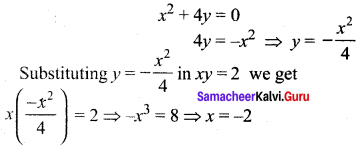

Question 10.
Show that the two curves x2 – y2 = r2 and xy = c2 where c, r are constants, cut orthogonally.
Solution:
Let (x1, y1) be the point of intersection of the two curves
I Curve: x2 – y2 = r2
Differentiating w.r.to x
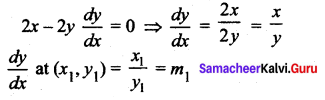
II Curve: xy = c2
Differentiating w.r.to x

![]()
Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.2 Additional Questions
Question 1.
Prove that the sum of the intercepts on the co-ordinate axes of any tangent to the curve x = a cos4 θ, y = a sin4 θ, 0 < θ < \(\frac{\pi}{2}\) is equal to a.
Solution:
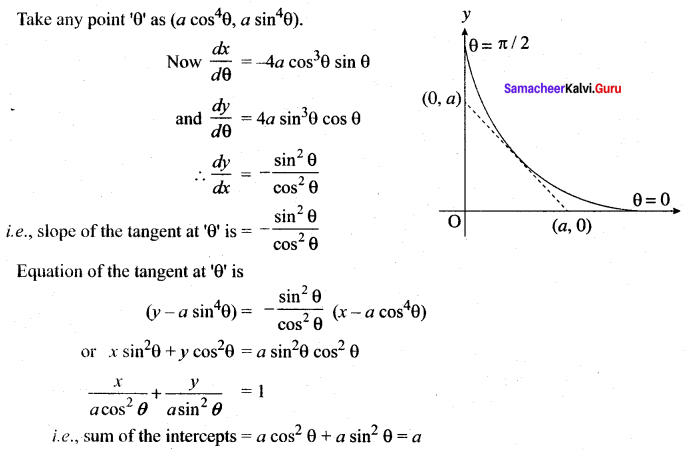
Question 2.
Find the equations of a normal to y = x3 – 3x that is parallel to 2x + 18y – 9 = 0.
Solution:
Let (x1, y,) be a point on the curve.

It is given that the normal is parallel to the line ⇒ m1 = m2

9y + 18 = -x – 2
x + 9y + 20 = 0
Question 3.
Prove that the curves 2x2 + 4y2 = 1 and 6x2 – 12y2 = 1 cut each other at right angles.
Solution:
Solving the given two equations,


Similarly it can be proved at the other points also.
Question 4.
Show that the equation of the normal to the curve x = a cos3 θ, y = a sin3 θ at ‘θ’ is x cos θ – y sin θ = a cos 2θ
Solution:

So, equation of the normal is
![]()
i.e. y sin θ – a sin4 θ = x cos θ – a cos4 θ
x cos θ – y sin θ = a cos4 θ – a sin4 θ
i.e.x cos θ – y sin θ = a[cos2 θ + sin2θ][cos2θ – sin2 θ]
= a[cos 2 θ]
So, the equation of the normai is x cos θ – y sin θ = a cos 2θ
![]()
Question 5.
If the curve y2 = x and xy = k are orthogonal, then prove that 8k2 = 1.
Solution:
y2 = x, xy = k
Solving the two equations, we get, (y2) (y) = k
y3 = k

Must Read: