You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.8
Question 1.
Find two positive numbers whose sum is 12 and their product is maximum.
Solution:
Let the two numbers be x, 12 – x.
Their product p = x (12 – x) = 12x – x2
To find the maximum product.
p'(x) = 12 – 2x
p”(x) = -2
p'(x) = 0 ⇒ 12 – 2x = 0 ⇒ 2x = 12
⇒ x = 6
at x = 6, p”(x) = -2 = -ve
⇒ p is maximum at x = 6
when x = 6, 12 – x = 12 – 6 = 6
So the two numbers are 6, 6
Question 2.
Find two positive numbers whose product is 20 and their sum is minimum.
Solution:
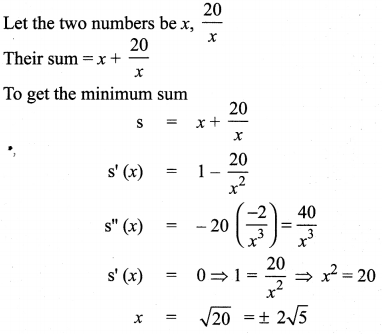
but x is positive (given)

![]()
Question 3.
Find the smallest possible value of x2 + y2 given that x + y = 10.
Solution:
Given x + y = 10 ⇒ 7 = 10 – x
To find the smallest value of x2 + y2

at x = 5, f”(x) = 4 at x = 5, y = 10 – 5 = 5 = +ve
x = 5 is a minimum point.
So the minimum value of x2 + y2 = 52 + 52 = 50
Question 4.
A garden is to be laid out in a rectangular area and protected by wire fence. What is the largest possible area of the fenced garden with 40 metres of wire.
Solution:
Perimeter = 40 m
2(l + b) = 40 ⇒ l + b = 20
Let l = x m
b = (20 – x)m
Area = l × b = x(20 – x) = 20x – x2
To find the maximum area
A(x) = 20x – x2
A'(x) = 20 – 2x
A”(x) = -2
A'(x) = 0 ⇒ 20 – 2x = 0
⇒ x = 10
x = 10 is a maximum point
:. Maximum Area = x (20 – x)
= 10(20 – 10)
= 10 × 10 = 100 sq.m.
Question 5.
A rectangular page is to contain 24 cm2 of print. The margins at the top and bottom of the page are 1.5 cm and the margins at other sides of the page is 1 cm. What should be the dimensions of the page so that the area of the paper used is minimum.
Solution:
Let the length of the printed page be = x cm
and breadth = y cm
Now xy = 24
⇒ y = \(\frac{24}{x}\)
The length of the paper = y + 3
Area A = (x + 2)(y + 3)
= xy + 3x + 2y + 6
= 24 + 3x + 2y + 6
= 3x + 2y + 30 ……. (2)
Substituting (1) in (2) we get
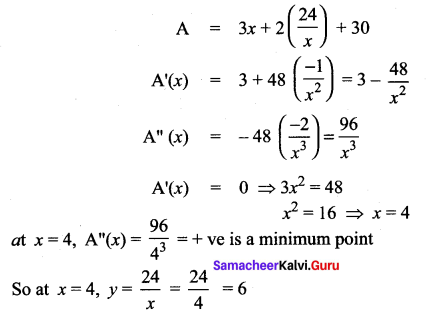
∴ Dimensions of the paper are
x + 2 = 4 + 2 = 6 cm
and y + 3 = 6 + 3 = 9 cm
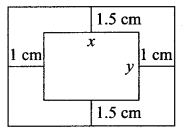
![]()
Question 6.
A farmer plans to fence a rectangular pasture adjacent to a river. The pasture must contain 1,80,000 sq. mtrs in order to provide enough grass for herds. No fencing is needed along the river. What is the length of the minimum needed fencing material?
Solution:
Given Area = 180000 sq. mtrs
Let length be = x
and breadth be = y

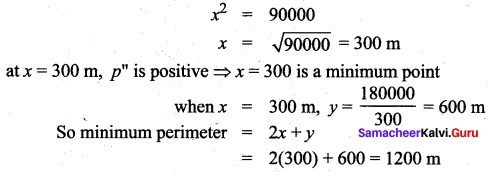
Question 7.
Find the dimensions of the rectangle with maximum area that can be inscribed in a circle of radius 10 cm.
Solution:
P is a point on the circumference of a circle of radius 10 cm P = (10 cos α, 10 sin α)
∴ PQ = 20 sinα and
PS = 20 cos α
A = area of PQRS = (20 sin α) (20 cos α)
= 400 sin α cosc α
= (200) (2 sin α cos α)
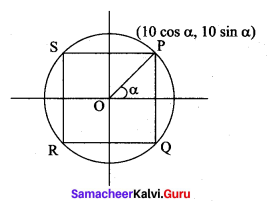

Question 8.
Prove that among all the rectangles of the given perimeter, the square has the maximum area.
Solution:
Let the length and breadth of the rectangle be x and y respectively.
P = 2(x + y) [given]
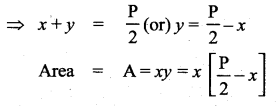
Substitute (3) in (2) we get

so x = 6 cm and y = 3 cm
Question 9.
Find the dimensions of the largest rectangle that can be inscribed in a semi circle of radius r cm.
Solution:
Let θ be the angle made by OP with the positive direction of x -axis.
Then the area of the rectangle A is
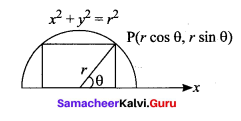
A(θ) = (2 r cos θ)(r sin θ)
= r2 2 sin θ cos θ = r2 sin 2θ
Now A(θ) is maximum when sin 2θ is maximum. The maximum value of
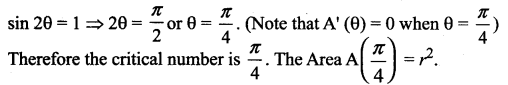
Question 10.
A manufacturer wants to design an open box having a square base and a surface area of 108 sq.cm. Determine the dimensions of the box for the maximum volume.
Solution:
Let the side of the square base be = x cm and the height be = y cm
Surface area = 108 sq cm
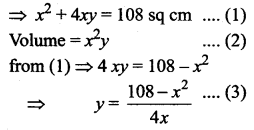
Substituting (3) in (2) we get

so x = 6 cm and y = 3 cm
![]()
Question 11.
The volume of a cylinder is given by the formula V = πr2h. Find the greatest and least values of V if r + h = 6.
Solution:
V = πr2h
Given r + h = 6 ⇒ h = 6 – r
V = πr2(6 – r) = 6πr2 – πr3

3πr(4 – r) = 0 ⇒ r = 0 or 4
when r = 4, h = 2
So v = π(16)(2) = 32π
when r = 0, V = 0
So the maximum volume = 32π and the minimum volume = 0
Question 12.
A hollow cone with base radius a cm and height b cm is placed on a table. Show that the
volume of the largest cylinder that can be hidden underneath is — times volume of the cone.
Solution:
The height of cone = h = b
The base radius = r = a
The base radius of cylinder = r
The height of cylinder = h

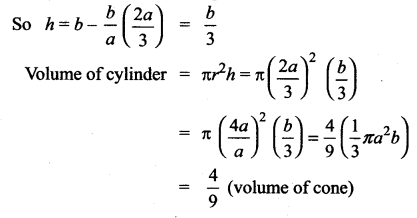
Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.8 Additional Problems
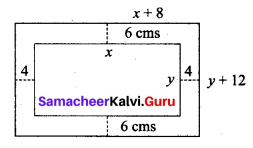
Question 1.
The top and bottom margins of a poster are each 6 cms and the side margins are each 4 cms. If the area of the printed material on the poster is fixed at 384 cms2, find the dimension of the poster with the smallest area.
Solution:
Let x and y be the length and breadth of printed area, then the area xy = 384
Dimensions of the poster area are (x + 8) and (y + 12) respectively.
Poster area A = (x + 8) (y + 12)
= xy + 12x + 8y + 96
= 12x + 8y + 480
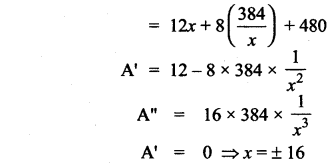
But x > 0
∴ x = 16
when x = 16, A” > 0
when x = 16, the area is minimum
y = 24
∴ x + 8 = 24,
y + 12 = 36
Hence the dimensions are 24 cm and 36 cm
Question 2.
Show that the volume of the largest right circular cone that can be inscribed in a sphere of radius a is \(\frac{8}{27}\) (volume of the sphere).
Solution:
Given that a is the radius of the sphere and let x be the base radius of the cone. If h is the height of the cone, then its volume is
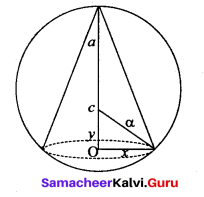
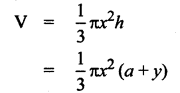
where OC = y so that height h = a + y
From the diagram x2 + y2 = a2
Using (2) in (1) we have
![]()
For the volume to be maximum:
![]()
⇒ 3y = + a or y = -a
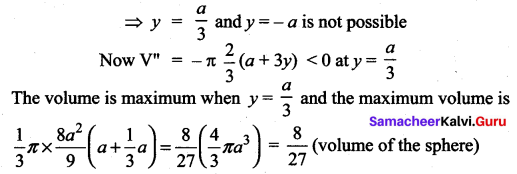
Question 3.
A closed (cuboid) box with a square base is to have a volume of 2000 c.c. The material for the top and bottom of the box is to cost Rs. 3 per square cm and the material for the sides is to cost Rs. 1.50 per square cm. If the cost of the materials is to be the least, find the dimensions of the box.
Solution:
Let x, y respectively denote the length of the side of the square base and depth of the box. Let C be the cost of the material
Area of the bottom = x2
Area of the top = x2
Combined area of the top and bottom = 2x2
Area of the four sides = 4xy
Cost of the material for the top and bottom = 3(2x)2
Cost of the material for the sides = (1.5)(4xy) = 6xy

Question 4.
Find two numbers whose sum is 100 and whose product is a maximum.
Solution:
Let the two numbers be x and y.
x + y = 100
⇒ y = 100 – x
Product = xy = x(100 – x)
f = x(100 – x) = 100x – x2
We have to find x at which f is maximum.

∴ f is maximum at x = 50
So, y = 100 – x = 100 – 50 = 50
So, the two numbers are 50, 50.
![]()
Question 5.
Find two positive numbers whose product is 100 and whose sum is minimum.
Solution:
Let the two numbers be x and y.
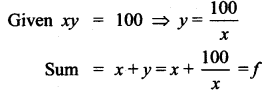
To find x at which f is maximum

So the two numbers are 10, 10.
Must Read: