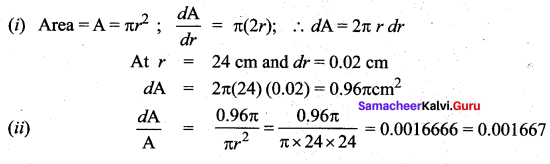Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.2

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.2

Question 1.
Find differential dy for each of the following functions:

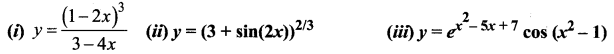
Solution:

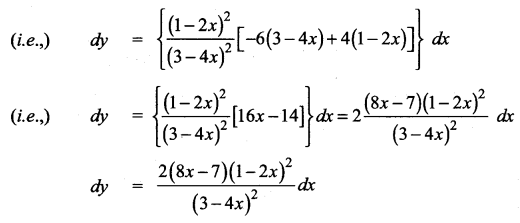
Question 2.
Find df for f(x) = x² + 3x and evaluate it for
(i) x = 2 and dx = 0.1
(ii) x = 3 and dx = 0.02
Solution:
y = f(x) = x² + 3x
dy = (2x + 3) dx
(i) dy {when x = 2 and ate = 0.1} = [2(2) + 3] (0.1)
= 7(0.1) = 0.7

(ii) dy {when x = 3 and dx = 0.02} = [2(3) + 3] (0.0.2)
= 9(0.02) = 0.18

Question 3.
Find ∆f and df for the function f for the indicated values of x, ∆x and compare
(i) f (x) = x³ – 2x² ; x = 2, ∆x = dx = 0.5
(ii) f(x) = x² + 2x + 3; x = -0.5, ∆x = dx = 0.1
Solution:
(i) y = f(x) = x³ – 2x²
dy = (3x² – 4x) dx
dy (when x = 2 and dx = 0.5) = [3(2²) – 4(2)] (0.5)
= (12 – 8)(0.5) = 4(0.5) = 2
(i.e.,) df = 2
Now ∆f = f(x + ∆x) – f(x)
Here x = 2 and ∆x = 0.5
f(x) = x³ – 2x²
So f(x + ∆x) = f(2 + 0.5) = f(2.5) = (2.5)³ – 2 (2.5)² = (2.5)² [2.5 – 2] = 6.25 (0.5) = 3.125
f(x) = f(2) = 2³ – 2(2²) = 8 – 8 = 0
So ∆f = 3.125 – 0 = 3.125

(ii) y = f(x) = x² + 2x + 3
dy = (2x + 2) dx
dy (when x = – 0.5 and dx = 0.1)
= [2(-0.5) + 2] (0.1)
= (-1 + 2) (0.1) = (1) (0.1) = 0.1
(i.e.,) df = 0.1
Now ∆f = f(x + ∆x) – f(x)
Here x = -0.5 and ∆x = 0.1
x² + 2x + 3
f(x + ∆x) = f(-0.5 + 0.1) = f(-0.4)
= (-0.4)² + 2(-0.4) + 3
= 0.16 – 0.8 + 3 = 3.16 – 0.8 = 2.36
f(x) = f(-0.5) = (-0.5)² + 2(-0.5) + 3
= 0.25 – 1 + 3 = 3.25 – 1 = 2.25
So ∆ f = f(x + ∆x) – f(x) = 2.36 – 2.25 = 0.11

Question 4.
Assuming log₁₀ e = 0.4343, find an approximate value of log₁₀ 1003.
Solution:
To find log 1003
1003 = 1000 + 3 and
log 1000 = 3
Let y = log x

Here x = 1000 and dx = 3 = 3 log₁₀e

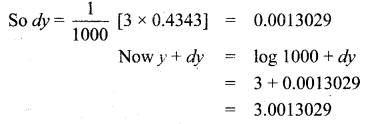
Question 5.
The trunk of a tree has diameter 30 cm. During the following year, the circumference grew 6 cm.
(i) Approximately, how much did the tree’s diameter grow?
(ii) What is the percentage increase in area of the tree’s cross-section?
Solution:
(i) Given r = 15 cm and rate of change of perimeter = 6 cm
To find the rate of change of diameter
Now perimeter = p = 2πr
So dp = 2πdr
Here dp = 6 cm (given)

Question 6.
An egg of a particular bird is very nearly spherical. If the radius to the inside of the shell is 5 mm and radius to the outside of the shell is 5.3 mm, find the volume of the shell approximately.
Solution:

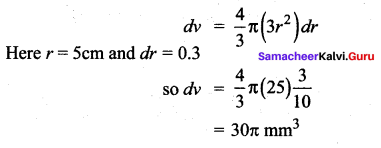
Question 7.
Assume that the cross section of the artery of human is circular. A drug is given to a patient to dilate his arteries. If the radius of an artery is increased from 2 mm to 2.1 mm, how much is cross-sectional area increased approximately?
Solution:
Area of circle = A = πr².

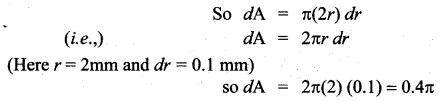
Question 8.
In a newly developed city, it is estimated that the voting population (in thousands) will increase according to V (t) = 30 + 12t² – t³, 0 ≤ t ≤ 8 where t is the time in years. Find the approximate change in voters for the time change from 4 to 4\(\frac{1}{6}\) year.
Solution:

Question 9.
The relation between the number of words y a person learns in x hours is given by y = 52\(\sqrt{x}\), 0 ≤ x ≤ 9. What is the approximate number of words learned when x changes from
(i) 1 to 1.1 hour?
(ii) 4 to 4.1 hour?
Solution:

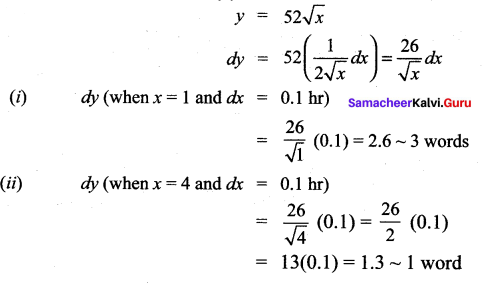
Question 10.
A circular plate expands uniformly under the influence of heat. If it’s radius increases from 10.5 cm to 10.75 cm, then find an approximate change in the area and the approximate percentage change in the area.
Solution:
Here radius is changing from 10.5 cm to 10.75 cm
⇒ r = 10.5 cm and dr = 0.25 cm
Now area = A = πr²
⇒ dA = π (2r) dr

(i) So dA
(when r = 10.5 cm and dr = 0.25 cm)
= π (2 × 10.5) (0.25)
= 5.25 π

Question 11.
A coat of paint of thickness 0.2 cm is applied to the faces of a cube whose edge is 10 cm. Use the differentials to find approximately how many cubic centimeters of paint is used to paint this cube. Also calculate the exact amount of paint used to paint this cube.
Solution:
(i) v = a³
so dv = a² da
dv (when) a = 10 cm and da = 0.20 cm
= 3(10²) (0.2)
300 × 0.2 = 60 cm³

Actual paint used = v at x + ∆x = 10.2 and x = 10 cm
= a³ at x + ∆x = 10.2 and x = 10
= (10.2)³ – (10) = 61.2 cm³

Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.2 Additional Questions

Question 1.
Find the differential dy and evaluate dy for the given values of x and dx. y = x⁴ – 3x² + x – 1, x = 2, dx = 0.1
Solution:

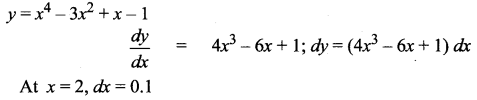
dy = [4(8) – 6(2) + 1] (0.1) = (32 – 12 + 1) (0.1)
= (21) (0.1) = 2.1
dy = (4x³ – 6x + 1)dx; dy = 2.1

Question 2.
Find the differential dy and evaluate dy for the given values of x and dx. y = \(\sqrt{1-x}\), x = 0, dx = 0.02
Solution:

Question 3.
The edge of a cube was found to be 30 cm with a possible error in measurement of 0.1 cm. Use differentials to estimate the maximum possible error in computing
(i) the volume of the cube and
(ii) the surface area of cube.
Solution:
The side of the cube = a = 30 cm
Error in a = da = 0.1 cm

Question 4.
The radius of a circular disc is given as 24 cm with a maximum error in measurement of 0.02 cm
(i) Use differentials to estimate the maximum error in the calculated area of the disc,
(ii) Compute the relative error.
Solution:
r = 24 cm,
dr = 0.02 cm