You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.1
Question 1.
Find an approximate value of \(\int_{1}^{1.5} x d x\) by applying the left-end rule with the partition {1.1, 1.2, 1.3, 1.4, 1.5}
Solution:
Here a = 1, b = 1.5, n = 5, f(x) = x
So, the width of each subinterval is
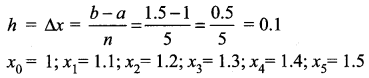
The left hand rule for Riemann sum,
S = [f(x0) + f(x1)) + f(x2) + f(x3) + f(x4)] ∆x
= [f(1) + f(1.1) + f(1.2) + f(1.3) + f(1.4)] (0.1)
= [1 + 1.1 + 1.2 + 1.3 + 1.4] (0.1)
= [6] (0.1)
= 0.6.
![]()
Question 2.
Find an approximate value of \(\int_{1}^{1.5} x^{2} d x\) by applying the right-end rule with the partition {1.1, 1.2, 1.3, 1.4, 1.5}.
Solution:
Here a = 1;
b = 1.5;
n = 5;
f(x) = x2
So, the width of each subinterval is
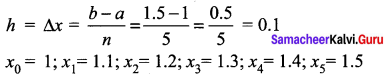
The Right hand rule for Riemann sum,
S = [f(x1) +f(x2) +f(x3) + f(x4) + f(x5)] ∆x
= [f(1.1) + f(1.2) + f(1.3) + f(1.4) + f(1.5)] (0.1)
= [1.21 + 1.44 + 1.69 + 1.96 + 2.25] (0.1)
= [8.55] (0.1)
= 0.855.
![]()
Question 3.
Find an approximate value of \(\int_{1}^{1.5}(2-x) d x\) by applying the mid-point rule with the partition {1.1, 1.2, 1.3, 1.4, 1.5}.
Solution:
Here a = 1;
b = 1.5;
n = 5;
f(x) = 2 – x
So, the width of each subinterval is
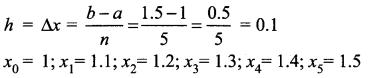
The mid-point rule for Riemann sum,
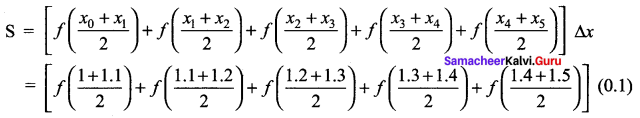
= [f(1.05) + f(1 .15) + f(1.25) +f(1.35) + f(1 .45)] (0.1)
= [0.95 + 0.85 + 0.75 + 0.65 + 0.55] (0.1)
= [3.75] (0.1)
= 0.375.