Samacheer Kalvi 7th Maths Guide Term 2 Chapter 2 அளவைகள் Ex 2.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 7th Maths Guide Pdf Term 2 Chapter 2 அளவைகள் Ex 2.4 Textbook Questions and Answers, Notes.

TN Board 7th Maths Solutions Term 2 Chapter 2 அளவைகள் Ex 2.4

பல்வகைத் திறனறி பயிற்சிக் கணக்குகள்

கேள்வி 1.
ஒரு மகிழுந்தின் (car) சக்கரம் 20 சுற்றுகளில் 3520 செ. மீ தொ-லைவைக் கடக்கிறது எனில், அதன் ஆரம் காண்க.
தீர்வு:

கேள்வி 2.
ஒரு வட்டவடிவக் குதிரைப் பந்தயக் களத்தினைச் சுற்றி வேலி அமைக்க, ஒரு மீட்டருக்கு ₹8 வீதம் மொத்தம் ₹2112 செலவாகிறது. அந்தக் குதிரைப் பந்தயக் களத்தின் (race course) விட்டம் காண்க.
தீர்வு:

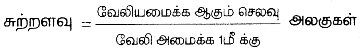
= \(\frac{2112}{8}\)
C = 264 மீ
2πr = 264 மீ (அல்லது)
πd = 264 மீ
\(\frac{22}{7}\) × d = 264
d = \(\frac{264 \times 7}{22}\)
d = 84மீ

கேள்வி 3.
நீளம் 120 மீ மற்றும் அகலம் 90மீ உள்ள ஒரு செவ்வக வடிவத் தோட்டத்தைச் சுற்றி 2மீ நீளமும், 1மீ அகலமும் உள்ள பாதை அமைக்கப்படுகிறது. அந்தப் பாதையின் பரப்பளவு காண்க.
தீர்வு:
வெளிச் உள்செவ்வகம் செவ்வகம்

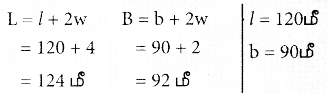
பாதையின் பரப்பு = LB – 1b ச.அ
= 124 × 92 – 120 × 90
= 11408 – 10800
= 608 மீ²

கேள்வி 4.
ஒரு வட்ட வடிவப் புல்வெளியைச் சுற்றி அலங்கரிக்க, ஒரு மீட்டருக்கு ₹55 வீதம் ₹16940. செலவாகிறது எனில், அதன் ஆரம் காண்க.
தீர்வு:

கேள்வி 5.
அருகிலுள்ள படத்தில் உள்ளபடி, ஒரு செவ்வகத்திற்குள் நான்கு வட்டங்கள் அடுத்தடுத்து உள்ளன. ஒரு வட்டத்தின் ஆரம் 3செ.மீ எனில், பின்வருவனவற்றைக் கணக்கிடுக.
(i) செவ்வகத்தின் பரப்பளவு
(ii) ஒரு வட்டத்தின் பரப்பளவு
(iii) செவ்வகத்திற்குள் நிழலிட்ட செவ்வகம் பகுதியின் பரப்பளவு

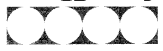
பரப்பளவு:
தீர்வு:

(i) செவ்வகத்தின் பரப்பளவு = 1b ச.அ
= 24 × 6
= 144 செ.மீ

(ii) ஒரு வட்டத்தின் பரப்பளவு = 2πr² ச.அ
= 3.14 × 3²
= 3.14 × 9
= 28.26 செ.மீ²

(iii) நிழலிடப்பட்ட பகுதியின் பரப்பளவு அலகுகள்
= செவ்வகத்தின் பரப்பளவு
4 × வட்டத்தின் பரப்பளவு ச.அ
= 144 – 4 × 28.26
= 144 – 113.04 C
= 30.96 செ.மீ²

மேற்சிந்தனைக் கணக்குகள்

கேள்வி 6.
ஒரு வட்டப் புல்வெளியைச் சுற்றி ஒரு வட்டப்பாதை அமைக்கப்படவுள்ளது. அந்தப் பாதையின் வெளிப்புற, உட்புறச் சுற்றளவுகள் முறையே 88செ.மீ, 44செ.மீ எனில், அந்த நடைப்பாதையின் அகலத்தையும் பரப்பளவையும் காண்க.
தீர்வு:

W = R – r = 14 = -7 = 7செ.மீ
நடைப்பாதையின் பரப்பு = π(R² – T²)
ச.அ
= π(R + r) (R – r)
= \(\frac{22}{7}\)(14 + 7)(14 – 7)

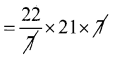
= 462செ.மீ²

கேள்வி 7.
76மீ நீளமும், 60மீ அகலமும் உள்ள ஒரு செவ்வக வடிவப் புல்வெளியின் மையத்தில், ஒரு மாடு 35மீ நீளமுள்ள கயிற்றால் கட்டப்பட்டுள்ளது. அந்த மாடு மேயமுடியாத நிலப்பரப்பளவை அளவிடுக.
தீர்வு:


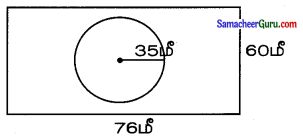
செவ்வகத்தின் பரப்பு 1b ச.அ
= 76 × 60
= 4560 மீ²
வட்டத்தின் பரப்பு = πr² ச.அ

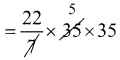
= 110 × 36
= 3850மீ²
மேய முடியாத நிலப்பரப்பு = செவ்வகத்தின் – வட்டத்தின் பரப்பு
= 4560 – 3850
= 710 மீ²

கேள்வி 8.
ஒரு, செவ்வக வயல்வெளியின் உட்புறமாக, 5மீ அகலமான நடைபாதை உள்ளது. வயல்வெளியின் நீளம், அதன் அகலத்தைப்போல் மூன்று மடங்காகும். நடைபாதையின் பரப்பளவு 500மீ² எனில், வயல்வெளியின் நீள, அகலங்களைக் காண்க.
தீர்வு:
W= 5மீ
நடைபாதையின் பரப்பு = 500மீ², l = 3bமீ
LB – lb = 500
(1 + 2w) (b +2w) – lb = 500
(3b + 10) (b + 10) – 3b(b) = 500

100 + 40b = 500
40b = 500 – 100
40b = 40°
b = \(\frac{400}{40}\)
b = 10 செ.மீ
நீளம் = 3b
= 3 × 10
l = 30 செ.மீ

கேள்வி 9.
ஒரு வட்ட வடிவத் திடலைச் சுற்றி, வட்டப்பாதை அமைக்கப்படுகிறது.
அதன் வெளிப்புற மற்றும் உட்புற வட்டங்களின் பரப்பளவு முறையே
1386மீ², 616மீ² எனில், அந்த
வட்டப்பாதையின் அகலத்தையும் பரப்பளவையும் காண்க.
தீர்வு:
வெளிவட்டத்தின் பரப்பு = 1386 மீ²
உள்வட்டத்தின் பரப்பு = 616 மீ²
வட்டப்பாதையின் பரப்பு =
வெளிவட்டத்தின் பரப்பளவு – உள்வட்டத்தின் பரப்பு ச.அ
= 1386 – 616
= 770மீ²
வெளிவட்டத்தின் பரப்பு = 1386 மீ²
πR² = 1386
\(\frac{22}{7}\) × R² = 1386
R² = \(\frac{1386 \times 7}{22}\) = 441
R = 21மீ
உள்வட்டத்தின் பரப்பு = 616மீ²
πr² = 616
\(\frac{22}{7}\) × r² = 616 ⇒ r² = \(\frac{616 \times 7}{22}\)
r² = 196
r = 14
பாதையின் அகலம் = R – r = 21 – 14 = 7மீ

கேள்வி 10.
52மீ ஆரமுள்ள ஒரு வட்ட வடிவமுள்ள புல்வெளியின் மையத்திலிருந்து 45மீ நீளமுள்ள ஒரு கயிற்றால் கட்டப்பட்டுள்ளது. அந்த ஆட்டால் மேயமுடியாத புல்வெளியின் பரப்பளவு காண்க.
தீர்வு:
R = 52
r = 45
மேயமுடியாத பகுதியின் பரப்பு = π(R² – r²) ச.அ
= π(R – r) (R – r)
= \(\frac{22}{7}\) (52 + 45) (52 – 45)

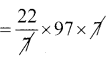
= 2134 மீ²

கேள்வி 11.
30செ.மீ × 20செ.மீ பரிமாணமுள்ள ஒரு செவ்வக அட்டையின் பக்க விளிம்பிலிருந்து 4செ.மீ அகலம் உள்ள பகுதி வெட்டியெடுக்கப்படுகிறது
எனில், அந்த வெட்டப்பட்ட பகுதியின் பரப்பளவு காண்க. மேலும்,
அட்டையின் மீதமுள்ள பகுதியின் பரப்பளவு காண்க.
தீர்வு:
L = 30 செ.மீ W = 4 செ.மீ
B = 20 செ.மீ
l = L – 2w = 30 – 2 × 4 = 30 – 8 = 22செ.மீ
b = B – 2w = 20 – 2 × 4 = 10 – 8 = 12செ.மீ
மீதமுள்ள அட்டையின் பரப்பு = LB – lb ச.அ
= 30 × 20 – 22 × 12
= 600 – 264
= 336 செ.மீ²
மீதமுள்ள அட்டையின் பரப்பு = lb ச.அ
= 22 × 12
= 264செ.மீ²

கேள்வி 12.
ஒரு செவ்வக நிலத்தின் பரிமாணங்கள் ஆடு 20மீ × 15மீ. அதன்மையம் வழியாகவும், இரு பக்கங்களுக்கு இணையாகவும் இருக்குமாறு இரண்டு பாதைகள் உள்ளன. நீளமாக உள்ள பாதையின் அகலம் 2மீ மற்றும் குறைந்த நீளமுள்ள பாதையின் அகலம் 1மீ எனில், கீழ்க்கண்டவற்றைக் காண்க.
(i) பாதைகளின் பரப்பளவு
(ii) நிலத்தின் மீதமுள்ள பகுதியின் பரப்பளவு
(iii) ஒரு ச.மீட்டருக்கு ₹10
வீதம் பாதையில் சாலை அமைக்க ஆகும் மொத்தச் செலவு.
தீர்வு:

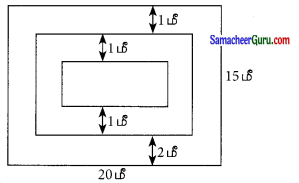
l = 20செ.மீ
b = 15மீ
நிலத்தின் பரப்பு = 1 × b ச.அ
= 20 × 15
= 300மீ²
நீளமான பாதையின் பரப்பு = 16 × 11
= 176மீ²
சிறிய பாதையின் பரப்பு = 14 × 9
= 126மீ²

(i) பாதையின் பரப்பளவு = 176 – 126
= 50மீ²

(ii) மீதமுள்ள பகுதியின் பரப்பு = 300 – 50
= 250 மீ²

(iii) 1 சமீ க்கு ஆகும் செலவு = ₹10
50 சமீ க்கு ஆகும் செலவு = ₹10 × 50
= ₹ 500