Tamilnadu State Board New Syllabus Samacheer Kalvi 7th Maths Guide Pdf Term 2 Chapter 4 வடிவியல் Ex 4.2 Textbook Questions and Answers, Notes.
TN Board 7th Maths Solutions Term 2 Chapter 4 வடிவியல் Ex 4.2
கேள்வி 1.
∆ABC ≅ ∆DEF எனக் கொடுக்கப்பட்டுள்ளது எனில்,
(i) ஒத்த பக்கங்களை எழுதுக.
தீர்வு:
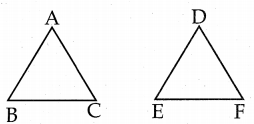
ஒத்த பக்கங்கள்
AB, DE;
BC, EF;
AC, DF
(ii) ஒத்த கோணங்களை எழுதுக.
தீர்வு:

ஒத்த கோணங்கள்
∠ABC, ∠DEF
∠BCA, ∠EFD
∠CAB, ∠FDE
![]()
கேள்வி 2.
கொடுக்கப்பட்ட முக்கோணங்கள் சர்வசமம் எனில்
(i) ஒத்த பக்கங்களை எழுதுக.
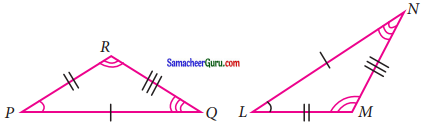
தீர்வு:
ஒத்த பக்கங்கள்
\(\overline{\mathrm{PQ}} \cong \overline{\mathrm{LN}}, \overline{\mathrm{PR}} \cong \overline{\mathrm{LM}}, \overline{\mathrm{RQ}}=\overline{\mathrm{MN}}\)
சர்வ சமக் கோணங்கள்
∠RPO = ∠NLM, ∠PQR = ∠LNM, ∠PRQ = ∠LMN
(ii) சர்வசமக் கோணங்களை எழுதுக.
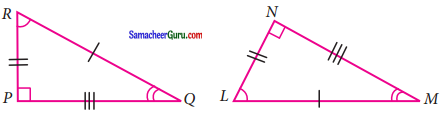
தீர்வு:
ஒத்த பக்கங்கள்
\(\overline{\mathrm{QR}} \cong \overline{\mathrm{LM}}, \overline{\mathrm{RP}} \cong \overline{\mathrm{LN}}, \overline{\mathrm{PQ}}=\overline{\mathrm{MN}}\)
சர்வ சமக் கோணங்கள்
∠PQR = ∠LMN, ∠QRP = ∠MLN, ∠RPQ = ∠LNM
![]()
கேள்வி 3.
∆ABC மற்றும் ∆EFG ஆகியன சர்வசம் முக்கோணங்கள் எனில், கொடுக்கப்பட்ட சோடி பக்கங்களும், சோடிக் கோணங்களும் ஒத்தவையா எனக் கூறுக.
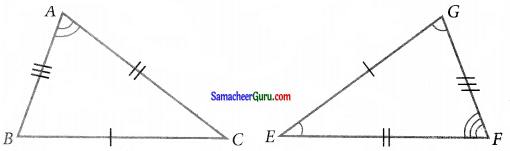
(i) ∠A மற்றும் ∠G
தீர்வு:
∠A மற்றும் ∠G ஒத்த கோணங்கள் அல்ல.
(ii) ∠B மற்றும் ∠E
தீர்வு:
∠B மற்றும் ∠E ஒத்த கோணங்கள் அல்ல.
(iii) ∠B மற்றும் ∠G
தீர்வு:
∠B மற்றும் ∠G ஒத்த கோணங்கள்
(iv) \(\overline{\mathrm{AC}}\) மற்றும் \(\overline{\mathrm{GF}}\)
தீர்வு:
\(\overline{\mathrm{AC}}\) மற்றும் \(\overline{\mathrm{GF}}\) ஒத்த பக்கங்கள் அல்ல
(v) \(\overline{\mathrm{BA}}\) மற்றும் \(\overline{\mathrm{FG}}\)
தீர்வு:
\(\overline{\mathrm{BA}}\) மற்றும் \(\overline{\mathrm{FG}}\) ஒத்த பக்கங்கள்
(vi) \(\overline{\mathrm{EF}}\) மற்றும் \(\overline{\mathrm{BC}}\)
தீர்வு:
\(\overline{\mathrm{EF}}\) மற்றும் \(\overline{\mathrm{BC}}\) ஒத்த பக்கங்கள் அல்ல
![]()
கேள்வி 4.
கொடுக்கப்பட்ட இரு முக்கோணங்களும் சர்வசம முக்கோணங்களா எனக் கூறுக விடைக்குத் தகுந்த காரணத்தைக் கூறுக.
(i)
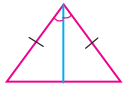
தீர்வு:
ப-கோ-ப விதிப்படி சர்வசம முக்கோணங்கள்
(ii)
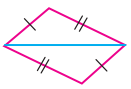
தீர்வு:
ப-ப-ப விதிப்படி சர்வசம முக்கோணங்கள்
(iii)
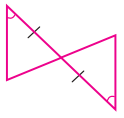
தீர்வு:
செ-க-ப விதிப்படி சர்வசம முக்கோணங்கள்
(iv)
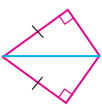
தீர்வு:
செ-க-ப விதிப்படி சர்வசம முக்கோணங்கள்
(v)
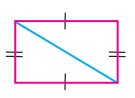
தீர்வு:
ப-ப-ப (அ) செ.க.ப (அ) ப-கோ-ப விதிப்படி சர்வசம முக்கோணங்கள்
![]()
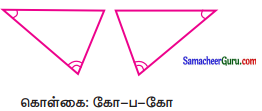
கேள்வி 5.
கொடுக்கப்பட்ட கொள்கையைப் பயன்படுத்தி சர்வசமத்தன்மையை முடிவு செய்வதற்குத் தேவைப்படும் விவரத்தைக் கீழே கொடுக்கப்பட்டுள்ள படங்களில் குறிக்க.
(i)
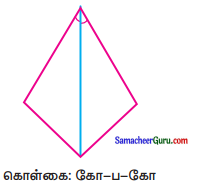
தீர்வு:
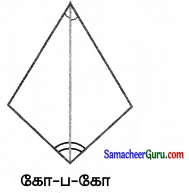
(ii)
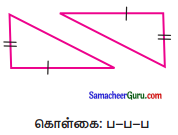
தீர்வு:
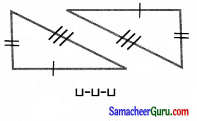
(iii)
தீர்வு:
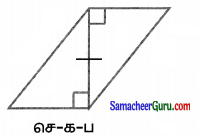
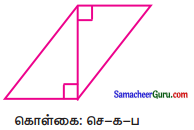
(iv)
தீர்வு:
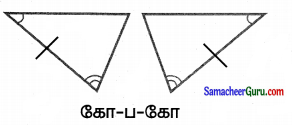
(v)
தீர்வு:
![]()
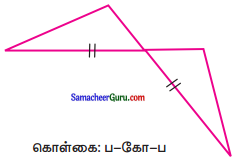
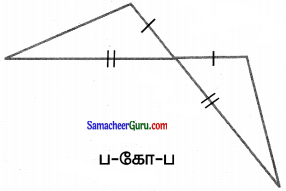
கேள்வி 6.
பின்வரும் முக்கோணங்களின் சர்வசமத் தன்மையை உறுதி செய்வதற்குப் பயன்படும் கொள்கையைக் குறிப்பிடுக.
(i)
தீர்வு:
ப-ப-ப
(ii)
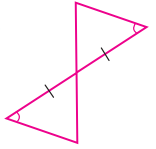
தீர்வு:
கோ-ப-கோ.
(iii)
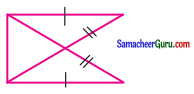
தீர்வு:
செ-க-பா
(iv)
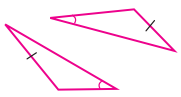
தீர்வு:
கோ-ப-கோ
(v)

தீர்வு:
கோ-ப-கோ
(vi)
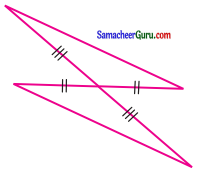
தீர்வு:
ப-கோ -ப
![]()
கேள்வி 7.
I. கொடுக்கப்பட்ட விவரங்களைக் கொண்டு XYZ என்ற முக்கோணத்தை அமைக்க.
(i) XY = 6.4 செ.மீ, ZY = 7.7 செ.மீ, மற்றும் XZ = 5 செ.மீ
தீர்வு:
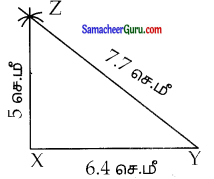
படி 1: ஒரு நேர்கோடு வரைக XY = 6.4 செ.மீ உள்ளவாறு கோட்டின் மீது X மற்றும் Y ஐ குறிக்க
படி 2: ஆரம் 5 செ.மீ உள்ளவாறு X ஐ மையமாகக் கொண்டு ஒரு வட்டவில்லை XYக்கு மேற்புறம் வரைக.
படி 3: Y ஐ மையமாகக் கொண்டு 7.7செ.மீ ஆரம் கொண்ட வட்டவில்லை முன்னர் வரைந்த வட்டவில்லை வெட்டுமாறு வரைக. வெட்டும் புள்ளியை Z எனக் குறிக்க.
படி 4: XZ மற்றும் YZ ஐ இணைக்க
XYZ தேவையான முக்கோணம் ஆகும்.
(ii) 7.5 செ.மீ பக்க அளவு கொண்ட சமபக்க முக்கோணம்
தீர்வு:
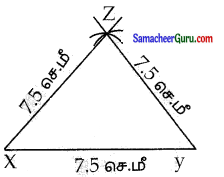
படி 1: ஒரு நேர்கோடு வரைக XY = 7.5 செ.மீ உள்ளவாறு கோட்டின் மீது X மற்றும் Y ஐ குறிக்க
படி 2: ஆரம் 7.5 செ.மீ உள்ளவாறு X ஐ மையமாகக் கொண்டு ஒரு வட்ட வில்லை XYக்கு மேற்புறம் வரைக.
படி 3: Y ஐ மையமாகக் கொண்டு 7.5செ.மீ ஆரம் கொண்ட வட்டவில்லை முன்னர் வரைந்த வட்டவில்லை வெட்டுமாறு வரைக. வெட்டும் புள்ளியை Z எனக் குறிக்க.
படி 4: XZ மற்றும் YZ ஐ இணைக்க
XYZ தேவையான முக்கோணம் ஆகும்.
![]()
iii) 4.6 செ.மீ அளவை சமபக்கங்களாகக் கொண்டு, 6.5 செ.மீ அளவை மூன்றாவது பக்கமாகக் கொண்ட இருசமபக்க முக்கோணம்.
தீர்வு:
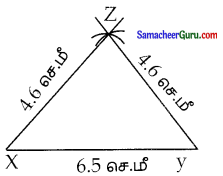
படி 1: ஒரு நேர்கோடு வரைக XY = 6.5 செ.மீ உள்ளவாறு கோட்டின் மீது X மற்றும் Y ஐ குறிக்க
படி 2: ஆரம் 4.6 செ.மீ உள்ளவாறு X ஐ மையமாகக் கொண்டு ஒரு வட்ட வில்லை XYக்கு மேற்புறம் வரைக.
படி 3: Y ஐ மையமாகக் கொண்டு 4.6செ.மீ ஆரம் கொண்ட வட்டவில்லை முன்னர் வரைந்த வட்டவில்லை வெட்டுமாறு வரைக. வெட்டும் புள்ளியை Z எனக் குறிக்க.
படி 4: XZ மற்றும் YZ ஐ இணைக்க
XYZ தேவையான முக்கோணம் ஆகும்.
II. கொடுக்கப்பட்ட விவரங்களைக் கொண்டு ABC என்ற முக்கோணத்தை அமைக்க
(i) AB = 7 செ.மீ, AC = 6.5 செ.மீ மற்றும் ZA = 120°.
தீர்வு:
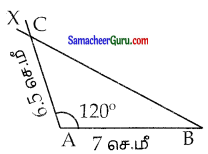
படி 1: ஒரு நேர்கோடு வரைக AB = 7 செ.மீ உள்ளவாறு A மற்றும் B என்ற புள்ளிகளை அதன் மீது குறிக்க
படி 2: A ல் AB உடன் 120° கோணத்தை அமைக்குமாறு AX என்ற கதிரை வரைக.
படி 3: A ஐ மையமாகக் கொண்டு 6.5செ.மீ ஆரம் கொண்ட வட்டவில்லைக் கதிர் AX ஐ வெட்டுமாறு வரைக. வெட்டும் புள்ளியை C எனக் குறிக்க
படி 4: BC ஐ இணைக்க.
ABC என்பது தேவையான முக்கோணம் ஆகும்.
![]()
(ii) BC = 8 செ.மீ, AC = 6 செ.மீ மற்றும் ZC = 40°.
தீர்வு:
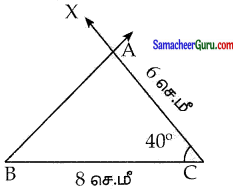
படி 1: ஒரு நேர்கோடு வரைக BC = 8 செ.மீ உள்ளவாறு B மற்றும் என்ற C புள்ளிகளை அதன்மீது குறிக்க.
படி 2: C ல் BC உடன் 40° கோணத்தை அமைக்குமாறு CX என்ற கதிரை வரைக.
படி 3: C ஐ மையமாகக் கொண்டு 6செ.மீ ஆரம் கொண்ட வட்டவில்லைக் கதிர் CX ஐ வெட்டுமாறு வரைக. வெட்டும் புள்ளியை A எனக் குறிக்க
படி 4: AC ஐ இணைக்க.
ABC என்பது தேவையான முக்கோணம் ஆகும்.
(iii) 5 செ.மீ அளவைச் சமபக்கங்களாகக் கொண்ட இரு சமபக்க விரிகோண முக்கோணம்.
தீர்வு:
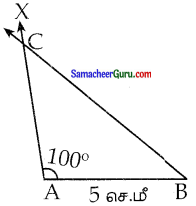
படி 1: ஒரு நேர்கோடு வரைக. AB = 5 செ.மீ உள்ளவாறு A மற்றும் B என்ற புள்ளிகளை அதன்மீது குறிக்க.
படி 2: Aல் AB உடன் 100° கோணத்தை அமைக்குமாறு AX என்ற கதிரை வரைக.
படி 3: A ஐ மையமாகக் கொண்டு 5 செ.மீ ஆரம் கொண்ட வட்ட வில்லைக் கதிர் AX வெட்டுமாறு வரைக. வெட்டும் புள்ளியை C எனக் குறிக்க.
படி 4: BC ஐ இணைக்க.
ABC என்பது தேவையான முக்கோணம் ஆகும்.
![]()
III. கொடுக்கப்பட்ட விவரங்களுக்கு PQR என்ற முக்கோணத்தை அமைக்க.
(i) ∠P = 60°, ∠R = 35 மற்றும் PR = 7.8 செ.மீ
தீர்வு:
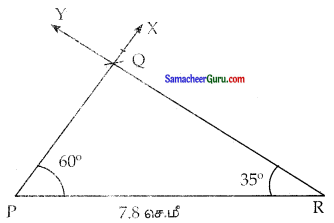
படி 1: ஒரு நேர்கோடு வரைக PR = 7.8 செ.மீ உள்ளவாறு P மற்றும் R என்ற புள்ளிகளை அதன் மீது குறிக்க.
படி 2: Pல் PR உடன் 60° கோணத்தை ஏற்படுத்துமாறு கதிர் PX வரைக.
படி 3: Rல் PR உடன் 35° கோணத்தை ஏற்படுத்துமாறு கதிர் RY வரைக
60° இரு கதிர்களும், வெட்டிக் கொள்ளும் புள்ளியை Q எனக் குறிக்க PQR என்பது தேவையான முக்கோணம் ஆகும்.
(ii) ∠P = 115′, ∠Q = 40° மற்றும் PQ = 6 செ.மீ
தீர்வு:
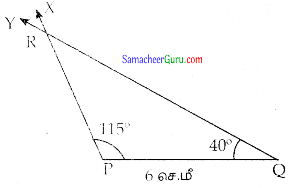
படி 1: ஒரு நேர்கோடு வரைக PQ = 6செ.மீ உள்ளவாறு P மற்றும் Q என்ற புள்ளிகளை அதன் மீது குறிக்க.
படி 2: Pல் PQ உடன் 115° கோணத்தை ஏற்படுத்துமாறு கதிர் PX வரைக.
படி 3: Qல்PQஉடன்40° கோணத்தை ஏற்படுத்துமாறு கதிர் QY வரைக இரு கதிர்களும், வெட்டிக் கொள்ளும் புள்ளியை R எனக் குறிக்க PQR என்பது தேவையான முக்கோணம் ஆகும்.
![]()
(iii) ∠Q = 90°, ∠R = 42° மற்றும் QR = 5.5 செ.மீ
தீர்வு:
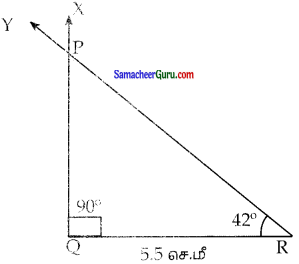
படி 1: ஒரு நேர்கோடு வரைக QR = 5.5செ.மீ உள்ளவாறு Q மற்றும் R என்ற புள்ளிகளை அதன் மீது குறிக்க.
படி 2: Qல் QR உடன் 90° கோணத்தை ஏற்படுத்துமாறு கதிர் QX வரைக.
படி 3: Rல் QR உடன் 42° கோணத்தை ஏற்படுத்துமாறு கதிர் RY வரைக இரு கதிர்களும், வெட்டிக் கொள்ளும் புள்ளியை P எனக் குறிக்க PQR என்பது தேவையான முக்கோணம் ஆகும்.
கொள்குறி வகை வினாக்கள்
கேள்வி 8.
இரு தள உருவங்கள் சர்வசமம் எனில், அவை
(i) சம அளவு உடையவை
(ii) சம வடிவம் உடையவை
(iii) சமகோண அளவு உடையவை
(iv) சம அளவும் சம வடிவமும் உடையவை
விடை:
(iv) சம அளவும் சம வடிவமும் உடையவை
கேள்வி 9.
பின்வருவனவற்றுள் எது, தள உருவங்களின் சர்வசமத் தன்மையைச் சோதிக்கப் பயன்படுகிறது.
(i) நகர்த்தல் முறை
(ii) மேற்பொருத்தும் முறை
(iii) பதிலிடும் முறை
(iv) நகர்த்திப் பொருத்தும் முறை
விடை:
(ii) மேற்பொருத்தும் முறை
![]()
கேள்வி 10.
எந்தக் கொள்கையின்படி இரு முக்கோணங்கள் சர்வசம முக்கோணங்களாக அமையா?
(i) ப-ப-ப கொள்கை
(ii) ப-கோ-ப கொள்கை
(iii) ப-ப-கோ கொள்கை
(iv) கோ-ப-கோ கொள்கை
விடை:
(iii) ப-ப-கோ கொள்கை
கேள்வி 11.
இரு மாணவர்கள் நேர்கோட்டுத் துண்டுகளை வரைந்தார்கள். அவை சர்வசமமாக இருப்பதற்கான நிபந்தனை என்ன?
(i) அவை அளவுகோலைப் பயன்படுத்தி வரையப்பட்டிருத்தல் வேண்டும்.
(ii) அவை ஒரே தாளில் வரையப்பட்டிருத்! தல் வேண்டும்.
(iii) அவை வெவ்வேறு அளவுடையவையாக இருத்தல் வேண்டும்.
(iv) அவை சம அளவுடையவையாக x இருத்தல் வேண்டும்
விடை:
(iv) அவை சம அளவுடையவையாக இருத்தல் வேண்டும்
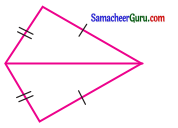
கேள்வி 12.
கொடுக்கப்பட்டுள்ள படத்தில் AD = CD மற்றும் AB = CB எனில், சம அளவு கொண்ட மூன்று சோடிகள் எவை?
(i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, ∠DAB = ∠DCB
(ii) AD = AB, DC = CB, ∠ADB = ∠CDB
(iii) AB = CD, AD = BC, ∠ABD = ∠CBD
(iv) ∠ADB = ∠CDB, ∠ABD =
∠CBD, ∠DAB = ∠DBC
விடை:
(i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, ∠DAB = ∠DCB
![]()
கேள்வி 13.
∆ABC மற்றும் ∆PQR இல் , ∠A = 50° = ∠P, PQ = AB மற்றும் PR = AC எனில், எந்தக் கொள்கையின்படி ∆ ABC உம் ∆ PQR உம் சர்வசமம் ஆகும்?
(i) ப-ப-ப கொள்கை
(ii) ப-கோ-ப கொள்ளை
(iii) கோ-ப-கோ கொள்கை
(iv) செ-க-ப கொள்கை
விடை:
(ii) ப-கோ-ப கொள்கை