Tamilnadu State Board New Syllabus Samacheer Kalvi 7th Maths Guide Pdf Term 2 Chapter 4 வடிவியல் Ex 4.3 Textbook Questions and Answers, Notes.
TN Board 7th Maths Solutions Term 2 Chapter 4 வடிவியல் Ex 4.3
பல்வகைத் திறனறி பயிற்சிக் கணக்குகள்
கேள்வி 1.
இரு சமபக்க முக்கோணத்தின் ஒரு கோணம் 76° மற்றும் இரு கோணங்கள் சமமெனில் அக்கோணங்களைக் காண்க.
தீர்வு:
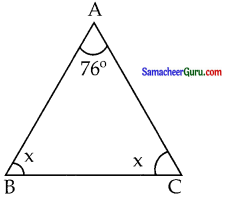
∠A + ∠B + ∠C = 180°
(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)
76 + x + x = 180
2x = 180 – 76
2x = 104
x = \(\frac{104}{2}\)
x = 52°
∠B = 52° ∠C = 52°
![]()
கேள்வி 2.
ஒரு முக்கோணத்தின் இரண்டு கோணங்கள் 46° எனில், அது எவ்வகை முக்கோணமாக இருக்கும்?
தீர்வு:
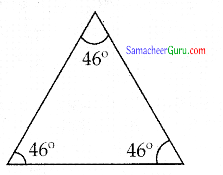
முக்கோணத்தில், இரண்டுகோணங்கள் சமம் எனில் அவை இரு சமபக்க முக்கோணமாகும்.
கேள்வி 3.
ஒரு முக்கோணத்தில் ஒரு கோணமானது மற்ற இரு கோணங்களின் கூடுதலுக்குச் சமமெனில். அம்முக்கோணத்தைக் குறித்து என்ன கூற இயலும்
தீர்வு:
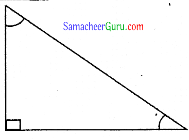
ஒரு முக்கோணத்தில் ஒரு கோணமானது மற்ற இரு கோணங்களின் கூடுதலுக்குச் சமமெனில் அம்முக்கோணம் ஒரு செங்கோண முக்கோணமாகும்.
![]()
கேள்வி 4.
ஒரு முக்கோணத்தில் ஒரு வெளிக்கோணம் 140° மற்றும் அதன் உள்ளெதிர்க் கோணங்கள் சமமெனில், அம்முக்கோணத்தின் அனைத்து உட்கோணங்களையும் காண்க.
தீர்வு:
∠A = x
∠B = X என்க
∠ACD = 140°
முக்கோணத்தின் இரு உள்கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு சமம்.
∠A + ∠B = ∠ACD
x + x = 140°
2x = 140°
x = \(\frac{140}{2}\) = 70
x = 70°
∠A = 70°, ∠B = 70°
∴ ∠A + ∠B + ∠C = 180°
(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)
70° + 70° ∠C = 180°
140 + ∠C = 180°
∠C = 180 – 140 = 40°
∠C = 40°
∠A = 70°, ∠B = 70°, ∠C = 40°
கேள்வி 5.
∆ JKL இல் ∠J = 60° மற்றும் ∠K = 40° எனில், L வழியாக KL ஐ நீட்டிப்பதால அமையும் வெளிக்கோணத்தின் அளவைக் காண்க.
தீர்வு:
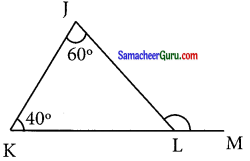
∠J = 60°
∠K = 40°
முக்கோணத்தில் இரு உள்கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு
∠JLM = ∠J + ∠K
= 60° + 40°
= 100°
![]()
கேள்வி 6.
கொடுக்கப்பட்டுள்ள படத்தில் x இன் மதிப்பைக் காண்க.
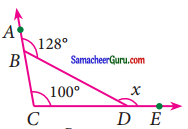
தீர்வு:
நேர்கோட்டிலமையும் அடுத்தடுத்த கோணங்களின் கூடுதல் 180° ஆகும். ∠ABD + ∠DBC = 180°
128 + ∠DBC = 180°
∠DBC = 180 – 128
∠DBC = 52°
முக்கோணத்தில் இரு உள்கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு சமம்.
∠B + ∠C = ∠BDE
52° + 100 = x
152 = x
x = 152°
கேள்வி 7.
∆MNO = ∆DEF, ∠M = 60° மற்றும் ∠E = 45° எனில் ∠0 இன் மதிப்பைக் காண்க.
தீர்வு:
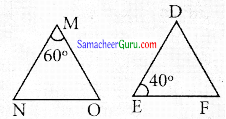
∠M = 60°
∠N மற்றும் ∠E ஒத்த கோணங்களாகும்.
∠N = ∠E = 45°
⇒ ∠N = 45°
முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180°
∠M + ∠N + ∠O = 1080 சமம்
60° + 45° + ∠O = 108°
105 + ∠O = 108°
∠O = 108° – 105
∠O = 75°
![]()
கேள்வி 8.
கொடுக்கப்பட்ட படத்தில் கதிர் ∠Z ஆனது ∠BAD மற்றும் ∠DCB இன் இருசமவெட்டி எனில்,
(i) ∆ BAC = ∆ DAC
(ii) AB = AD
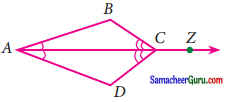
தீர்வு:
(i) முக்கோணம் BAC மற்றும் DAC (ZDBC = 52° படத்தில்,
∠DAC = ∠BAC
∠BCA = ∠DCAL
∴ AC = AC (பொதுபக்கம்
கோ-ப-கோ விதிப்படி ∆BAC ≅ ∆DAC
ii) AZ ஆனது ∠BAC ஐ இரு சமபாகமாக பிரிக்கிறது.
∴ AB = AD
கேள்வி 9.
படத்தில் FG = FI மற்றும் GI-ன் மையப்புள்ளி H எனில் AFGH = A FHI என நிறுவுக.
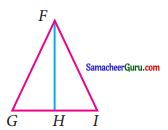
தீர்வு:
FG = FI
∠H = 90°
செ-க-ப விதிப்படி ∆FGH ≅ ∆ FHI நிரூபிக்கப்பட்டது.
கேள்வி 10.
படத்தில் கொடுக்கப்பட்டுள்ள முக்கோணங்கள் சர்வசமமா? AC ஆனது DE இக்கு இணையானது எனக் கூற இயலுமா?
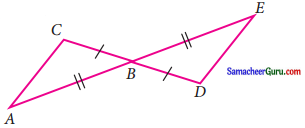
தீர்வு:
படத்திலிருந்து
CD = BD
AB = BE
மற்றும் AC = DE
ப-ப-ப விதிப்படி, முக்கோணங்கள் சர்வசமம் ஆகும் மற்றும் AC ஆனது DE க்கு இணையாகும்.
![]()
மேற்சிந்தனைக் கணக்குகள்
கேள்வி 11.
படத்தில் BD = BC எனில் X இன் மதிப்பைக் காண்க.
தீர்வு:
(i) முக்கோணத்தின் உள் இரு கோணத்தின் கூடுதல் அவற்றின் வெளிக் கோணத்திற்கு சமம்.
115° = 35° + ∠B
115 – 35 = ∠B
80 = ∠B
∠B = 80°
நேர்கோட்டில் அமையும் கோணத்தின் கூடுதல் = 180°
115° + ∠BCA = 180°
∠BCA = 180° – 115
∠BCA = 65°
படத்திலிருந்து
∠BDC = ∠BCD = 65°
∴ ∠BDA = 115°
∠BAD + ∠ABD + ∠BDA = 180°
35° + x + 115° = 180
x + 150 = 180
x = 180 – 150
x = 30°
கேள்வி 12.
கொடுக்கப்பட்டுள்ள படத்தில் X இன் மதிப்பைக் காண்க
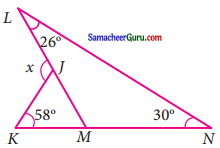
தீர்வு:
முக்கோணத்தில் கோணங்களின் கூடுதல் 180°
∠L + ∠N + ∠M = 180°
26° + 30° + ∠M = 180°
∠M = 180 – 56
∠M = 124°
நேர்கோட்டிலமையும் கோணத்தின் கூடுதல் 180°
∠LMN + ∠LMK = 180°
124° + ∠LMK = 180°
∠LMK = 180 – 124
ZLMK = 56°
முக்கோணத்தில் உள் எதிர்கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு சமம்.
x = 56° + 58°
x = 114°
![]()
கேள்வி 13.
கொடுக்கப்பட்டுள்ள படத்தில் X மற்றும் y இன் மதிப்பைக் காண்க.
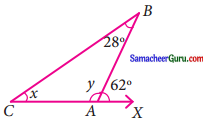
தீர்வு:
முக்கோணத்தில் இரு உள்கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு சமம்.
62° = x + 280
x = 62 – 28°
x = 34°
∠C + ∠A + ∠B = 180°
(முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180°)
x + y + 28 = 180°
34° + y + 28 = 180°
y + 62 = 180°
y = 180 – 62
y = 118°
கேள்வி 14.
∆DEF இல் ∠F = 48°, ∠E = 68° மற்றும் ∠D இன் கோண இருசமவெட்டியானது FE ஐ G இல் சந்திக்கிறது ∠FGD ஐக் காண்க.
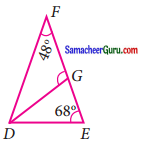
தீர்வு:
∆EFG, ∠E + ∠F + ∠D = 180°
(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)
68° + 48° + ∠D = 180
∠D = 180 – 116
∠D = 64°
கோணம் A ஐ DG ஆனது
இருசமவெட்டியாகும்.
∴ ∠FDG = \(\frac{1}{2}\) ∠FAE
= \(\frac{1}{2}\) × 64°
∠FDG = 32°
∆ DFG ல்,
32° + ∠FGD + 48° = 180
∠FGD + 80 = 180
∠FGD = 180 – 80
∠FGD = 100°
கேள்வி 15.
படத்தில் X இன் மதிப்பைக் காண்க.
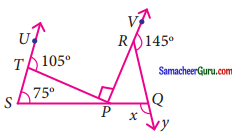
தீர்வு:
நேர்க்கோட்டிலமையும் கோணங்களின் கூடுதல் = 180°
105° + ∠RTS = 180
∠RTS = 180 – 105
∠RTS = 75°
75° + 75° + ∠TPS = 180
∠TPS = 180 – 150
∠TPS = 30°
நேர்க்கோட்டிலமையும் கோணங்களின் கூடுதல் = 180°
30° + 90° + ∠RPQ = 180
∠RPQ = 180 – 120
∠RPQ = 60°
நேர்க்கோட்டிலமையும் கோணங்களின் கூடுதல் = 180°
145° + ∠QRP = 180
∠QRP = 180 – 145
∠QRP = 35°
முக்கோணத்தின் உள் இரு கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு சமம்.
x = 60 + 35
x = 95°
![]()
கேள்வி 16.
கொடுக்கப்பட்டுள்ள படத்திலிருந்து y இன் மதிப்பைக் காண்க.
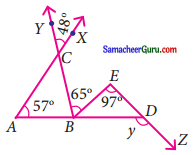
தீர்வு:
குத்தெதிர்கோணங்கள் சமம்.
∠ACB = 48°
∆ACB ல்
∠A + ∠B + ∠CBA = 180
57° + ∠B + 48° = 180
∠B = 180 – 105
∠B = 75°
நேர்க்கோட்டிலமையும் கோணங்களின் கூடுதல் = 180°
∠CBA + ∠CBE + ∠EBD = 180
75° + 65° + ∠EBD = 180°
∠EBD = 180 – 140
∠EBD = 40°
முக்கோணத்தில் இரு உள்கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு சமம்.
y = 97° + 40°
y = 137°