Samacheer Kalvi 7th Maths Guide Term 3 Chapter 2 சதவீதமும் தனி வட்டியும் Ex 2.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 7th Maths Guide Pdf Term 3 Chapter 2 சதவீதமும் தனி வட்டியும் Ex 2.5 Textbook Questions and Answers, Notes.

TN Board 7th Maths Solutions Term 3 Chapter 2 சதவீதமும் தனி வட்டியும் Ex 2.5

பலவகைத் திறனறி பயிற்சிக் கணக்குகள்

Question 1.
மதி தனது அடுக்குமாடிக் குடியிருப்பை வாங்கும்போது வைப்புத் தொகையை அதன் மதிப்பில் 10 இல் ஒரு பங்கைச் செலுத்தினார் எனில், வைப்புத் தொகையின் சதவீதம் காண்க.
தீர்வு :
வைப்பு தொகை = \(\frac{1}{10}\)

சதவீதம் = \(\frac{1}{10}\) × \(\frac{10}{10}\)

= \(\frac{10}{100}\) = 10%

Question 2.
ஒரு தேர்வில் யாழினி 25 இக்கு 15 மதிப்பெண்கள் பெற்றாள் எனில், அதன் சதவீதம் காண்க.
தீர்வு :
யாழினி பெற்ற மதிப்பெண்கள் = \(\frac{15}{25}\)

மதிப்பெண் சதவீதம் = \(\frac{15}{25}\) × \(\frac{4}{4}\)

= \(\frac{60}{100}\) = 60 %

Question 3.
ஒரு பள்ளியில் மொத்தமுள்ள 120 ஆசிரியர்களில் 70 ஆசிரியர்கள் ஆண்கள் எனில், ஆண் ஆசிரியர்களின் சதவீதத்தைக் காண்க.
தீர்வு :
மொத்த ஆசிரியர்கள் = 120
ஆண் ஆசிரியர்கள் = 70
ஆண் ஆசிரியர்களின் சதவீதம் = \(\frac{70}{120}\) × \(\frac{10}{10}\)

= \(\frac{700}{1200}\)

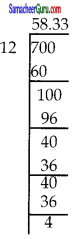
= \(\frac{700}{1200}\) % = 58.33 %

Question 4.
ஒரு மட்டைப் பந்து (கிரிக்கெட்) அணி ஒரு வருடத்தில் 70 போட்டிகளில் வெற்றியும் 28 போட்டிகளில் தோல்வியும் 2 போட்டிகளில் முடிவு ஏதுமில்லை எனவும் இருந்தால் அணியின் வெற்றிச் சதவீதத்தைக் கணக்கிடுக.
தீர்வு :
மொத்த போட்டிகளில் = 100
வெற்றி பெற்ற போட்டிகள் = 70
வெற்றி பெற்ற போட்டிகளின் சதவீதம் = \(\frac{70}{100}\) = 70 %

Question 5.
ஒரு கிராமப்புறப் பள்ளியில் 500 மாணவர்கள் பயின்று வருகின்றனர். அதில் 370 மாணவர்களுக்கு நீந்தத் தெரியும் எனில், நீந்தத் தெரிந்தவர்களின் சதவீதத்தையும், நீந்தத் தெரியாதவர்களின் சதவீதத்தையும் காண்க.
தீர்வு :
மொத்த மாணவர்கள் = 500
நீந்த தெரிந்த மாணவர்கள் = 370
சதவீதம் = \(\frac{370}{500}\)
= \(\frac{370}{5}\) %
= 74%
74% நீந்த தெரிந்தவர்கள்
26% நீந்த தெரியாதவர்கள்

Question 6.
சரளா என்பவரின் ஊதியத்திற்கும் சேமிப்பிற்கும் இடையேயுள்ள விகிதம் 4 : 1 எனில், அவரது சேமிப்பை சதவீதத்தில் கூறுக. தீர்வு :
ஊதியத்திற்கும் சேமிப்பிற்கும் உள்ள விகிதம் = 4 : 1
மொத்த விகிதம் = 5
சேமிப்பின் சதவீதம் = \(\frac{1}{5}\)
= \(\frac{1}{5}\) × \(\frac{20}{20}\)
= \(\frac{20}{100}\)
= 20 %

Question 7.
ஒரு விற்பனையாளர் அவர் செய்யும் விற்பனைத் தொகையில் 5% தரகாகப் பெறுகிறார். அவர் செய்த விற்பனை ₹ 1,500 எனில், அவர் பெறும் தரகு எவ்வளவு?
தீர்வு :
r = 5%
தொகை = ₹ 1500
தரகு தொகை = 1500 ல் 5%
= \(\frac{5}{100}\) × 1500
= 5 × 15
= ₹ 75

Question 8.
2015 ஆம் ஆண்டின் உலகக் கோப்டை கிரிக்கெட் போட்டிக்கான நுழைவுச்சீட்டு ₹ 1,500 ஆக இருந்தது. தற்போது அதன் விலை 18% ஆக உயர்ந்தால், நுழைவுச்சீட்டின் விலை எவ்வளவு?
தீர்வு :
தொகை = ₹ 1,500
கூடுதல் % = ₹ 1500 ல் 18%
= \(\frac{18}{15}\) × 1500
= 18 × 15 = 270
உயர்ந்த தொகை = 1500 + 270 = ₹ 1770

Question 9.
50 இல் 2 என்பது எவ்வளவு சதவீதமாகும்?
தீர்வு :
X என்பது சதவீதம் என்க
50 ல் x% = 2
\(\frac{50 \times x}{100}\) = 2
x = 2 × 2
x = 4%

Question 10.
8 உடன் எத்தனை சதவீதம் சேர்ந்தால் 64 கிடைக்கும்?
தீர்வு :
x என்பது சதவீதம் என்க.
8 ல் x% = 64
\(\frac{x}{100}\) × 8 = 64

x = \(\frac{64 \times 25}{2}\)

x = 32 × 25
x = 800 %

Question 11.
ஸ்டீபன் என்பவர் தனது வங்கியின் சேமிப்புக் கணக்கில் ₹ 10,000 ஐ 2% தனிவட்டி வீதத்தில் முதலீடு செய்தார் எனில், 4 ஆண்டுகளின் முடிவில் அவர் பெறும் தனிவட்டி எவ்வளவு?
தீர்வு :
P = ₹ 10000, r = 2%
n = 4 ஆண்டுகள்
SI = \(\frac{\mathrm{Pnr}}{100}\)

= \(\frac{100 \emptyset \emptyset \times 4 \times 2}{1 \emptyset \emptyset}\)
= 100 × 8
= ₹ 800

Question 12.
ரியா என்பவர் மகிழுந்து வாங்குவதற்காக ₹ 15,000 ஐ 10% தனிவட்டி என்ற வீதத்தில் கடனாகப் பெற்றார் அவர் ₹ 9,000 ஐக் கடனை முடிக்கும் தருவாயில், வட்டியாகச் செலுத்தினார் எனில், கடனைப் பயன்படுத்திய காலத்தைக் கணக்கிடுக.
தீர்வு :
P = ₹ 15000, தனி வட்டி = ₹ 9000
r = 10%
தனிவட்டி = \(\frac{\mathrm{Pnr}}{100}\)

9000 = \(\frac{15000 \times n \times 10}{100}\)

n = \(\frac{9000 \times 100}{15000 \times 10}\) = \(\frac{90}{15}\)
n = 6 ஆண்டுகள்

Question 13.
₹ 3,000 அசலுக்கு ஆண்டுக்கு 8% என வழங்கப்படும் தனிவட்டியானது ₹ 4,000 அசலுக்கு ஆண்டுக்கு 12% என 4 ஆண்டுகளுக்கு வழங்கப்படும் தனிவட்டிக்கு நிகராகும் காலம் என்ன?
தீர்வு :
P₁ = ₹ 3000
n₁ = x
X என்பது வருடங்களின் எண்ணிக்கை என்க
r₁ = 8y
P₂ = 4000
n₂ = 4 ஆண்டுகள்

\(\frac{\mathrm{p}_{1} \mathrm{n}_{1} \mathrm{r}_{1}}{100}=\frac{\mathrm{p}_{2} \mathrm{n}_{2} \mathrm{r}_{2}}{100}\)

y₂ = 12%

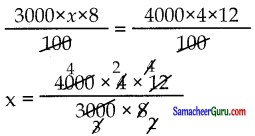
x = 8 ஆண்டுகள்

மேற்சிந்தனைக் கணக்குகள்

Question 14.
ஒரு நபர் தனது பயணத்தை 80கிமீ மகிழுந்திலும் 320 கி.மீ தொடர்வண்டியிலும் மேற்கொள்கிறார் எனில், மொத்தப் பயணத்தில் அவர் மகிழுந்தில் பயணம் செய்த தூரத்தின் சதவீதத்தையும் தொடர்வண்டியில் பயணம் செய்த தூரத்தின் சதவீதத்தையும் காண்க.
தீர்வு :
மகிழுந்தில் பயணித்த தொலைவு = 80 கிமீ
தொடர் வண்டியில் பயணித்த தொலைவு = 320 கிமீ
விகிதம் = \(\frac{80}{320}\) = \(\frac{1}{4}\)
மொத்த விகிதம் = 1 + 4 = 5
மகிழுந்தில் பயண தூர சதவீதம் = \(\frac{1}{5}\) × 100 = 20%
தொடர்வண்டியில் பயணதூர சதவீதம் = \(\frac{4}{5}\) × 100 = 80 %

Question 15.
இலலிதா என்பவர் கான் எழுதிய ஒரு கணிதத் தேர்வில் 35 சரியான பதில்களும் 10 தவறான பதில்களும் எழுதினார் எனில், அவர் அளித்த சரியான பதில்களின் சதவீதம் என்ன?
தீர்வு :
சரியான பதில்கள் = 35
தவறான பதில்கள் = 10
மொத்த பதில்கள் = 35 + 10 = 45
சரியான பதில்களின் சதவீதம் = \(\frac{35}{45}\) × 100

= \(\frac{700}{9}\)

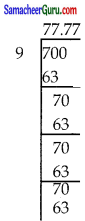
= 77.78 %

Question 16.
குமரன் ஆண்டுக்கு 7 மாதங்கள் வேலை செய்கிறார் எனில், அந்த ஆண்டில் அவர் எவ்வளவு சதவீதம் வேலை செய்தார் என்பதைக் கணக்கிடுக.
தீர்வு :
குமரன் வேலை செய்தது = 7 மாதங்கள்
ஆண்டுக்கு = 12 மாதங்கள்
58.33 செய்த வேலையின் சதவீதம் = \(\frac{7}{12}\) × 100

= \(\frac{7 \times 25}{3}\)

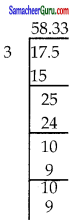
= 58.33%

Question 17.
ஒரு கிராமத்தின் மக்கள் தொகை 8000 இவர்களில் 80% பேர் கல்வியறிவு பெற்றவர்கள் அதில் 40% பெண்கள் எனில், கல்வியறிவு பெற்ற பெண்களின் எண்ணிக்கைக்கும் மொத்த மக்கள் தொகைக்கும் உள்ள உதவீதத்தைக் காண்க.
தீர்வு :
மொத்த மக்கள் தொகை = 8000
கல்வியறிவு பெற்றவர்கள் சதவீதம் = 80 %
கல்வியறிவு பெற்றவர்கள் = 8000 ல் 80 %
= \(\frac{80}{100}\) × 8000 = 6400

40 % பெண்கள் கல்வியறிவு பெற்றவர்கள் = 6400 ல் 40%
= \(\frac{40}{100}\) × 6400 = 25600

கல்வியறிவு பெற்ற பெண்களின் சதவீதம்
= \(\frac{25600}{8000}\) × 100

= \(\frac{25600}{80}\) %

= \(\frac{256}{8}\) % = 32 %

Question 18.
ஒரு மாணவர் 20 கேள்விகள் கெண்டகணிதத் தேர்வை எதிர்கொண்டு அதில் 80% மதிப்பெண்கள் பெற்றார் எனில், அவர் எத்தனை கேள்விகளுக்குச் சரியாகப் பதிலளித்தார்?
தீர்வு :
சரியான பதிலளித்தவர்களின் எண்ணிக்கை = 20 ல் 80%
= \(\frac{80}{100}\) × 20
= 8 × 2 = 16

Question 19.
8.5 கி.கி எடை கொண்ட ஓர் உலோகப் பட்டையில் 85% வெள்ளி எனில், அதில் வெள்ளியின் எடையைக் காண்க.
தீர்வு :
உலோகப் பட்டையின் எடை = 8.5கி.கி
வெள்ளி = 85%
வெள்ளியின் எடை = 8.5 கி.கில் 85 %

= \(\frac{85}{100}\) × 8.5

= \(\frac{85}{100}\) × \(\frac{85}{10}\)

= \(\frac{7225}{1000}\)

= 7.225 கி.கி

Question 20.
ஒரு தொடர்வண்டியில் பயணச்சீட்டின் முழுக்கட்டணம் ₹230 சலுகை அட்டை வைத்திருப்பவர்களுக்கு ₹ 120 இக்கு டிக்கெட் வழங்கப்பட்டால், சலுகை அட்டைதாரர்களுக்கு வழங்கப்பட்ட தள்ளுபடிச் சதவீதத்தைக் காண்க.
தீர்வு :
பயணச்சீட்டின் சலுகை = ₹ 120
மொத்த தொகை = ₹ 230
தள்ளுபடி = ₹ 230 – 120 = ₹ 110
தள்ளுபடி சதவீதம் = \(\frac{110}{230}\) × 100

= \(\frac{1100}{23}\)

= 47.82%

Question 21.
ஒரு தண்ணர் தொட்டியின் கொள்ளளவு 200 லிட்டர்கள் ஆகும். தற்போது அதில் 40 % தண்ணீ ர் நிரம்பியுள்ளது எனில், 75 % தண்ணீ ர் அதில் நிறைய வேண்டுமெனில் இன்னும் எத்தனை லிட்டர்கள் தண்ணீர் தேவைப்படும்?
தீர்வு :
தண்ணீர் தொட்டியின் கொள்ளவு = 200 லிட்டர்கள்
40% தண்ணீ ரின் கொள்ளவு = 200 ல் 40%
= \(\frac{40}{100}\) × 200
2 × 40 = 80 லிட்டர்கள்
75% தண்ணீர் நிறைய வேண்டுமெனால் அதன் கொள்ளவு 200 ல் 75%
= \(\frac{75}{100}\) × 200
= 75 × 2
= 150 லிட்டர்கள்
தேவைப்படும் நீரின் அளவு = 150 – 80 = 70 லிட்டர்கள்

Question 22.
இவற்றுள் எது பெரியது 16\(\frac{2}{3}\), அல்லது \(\frac{2}{5}\) அல்லது 0.17?
தீர்வு :
= 16\(\frac{2}{3}\) = \(\frac{50}{3}\), \(\frac{2}{5}\), 0.17 = \(\frac{17}{100}\)

\(\frac{50}{3} \times \frac{100}{100}=\frac{5000}{300}\) \(\frac{2}{5} \times \frac{60}{60}=\frac{120}{300}\) \(\frac{17}{100} \times \frac{3}{3}=\frac{51}{300}\)

16\(\frac{2}{3}\) – என்பதே பெரியது.

Question 23.
ஓர் இயந்திரத்தின் தற்போதைய மதிப்பு ₹ 1,62,000 ஒவ்வொரு ஆண்டுக்கும் இவ்வியந்திரத்தின் மதிப்பு – 10% குறைகிறது எனில், இரண்டு ஆண்டுகள் கழித்து அவ்வியந்திரத்தின் மதிப்பு என்ன ?
தீர்வு :
p = 1,62,000
r = 10 %
n = 2
A = P\(\left(1-\frac{r}{100}\right)^{2}\)

= 162000 (1 – \(\frac{10}{100}\))²

= 162000 (\(\frac{10-1}{3}\))²

= 162000 × (\(\frac{9}{10}\))²

= 162000 × \(\frac{81}{100}\)

= 16200 × 81 = 1,31,200

Question 24.
ஒரு தொகை ஒரு குறிப்பிட்ட தனிவட்டி வீதத்தில் 2 ஆண்டுகளில் ₹ 6,200 எனவும், 3 ஆண்டுகளில் 16,800 எனவும் உயர்கிறது. எனில் அந்தத் தொகையையும், வட்டி வீதத்தையும் காண்க.
தீர்வு :
P தொகை, R வட்டிவீதம்
∴ P+ (P × 2 × R/100) = 6200 ………. (1)
P + (P × 3 × R/100) = 6800 ……….. (2)
1& 2 ஐ தீர்க்க
\(\frac{3 \mathrm{PR}}{100}\) – \(\frac{2 \mathrm{PR}}{100}\) = 6800 – 6200 = 600

\(\frac{3 P R-2 P R}{100}\) = 600

PR = 600 × 100
PR = 60000

1 + 2p + 5 PR/100 = 15000 ……..(3)

PR = 60000 in 3
2P + 5 × 6000/100 = 15000
2P + 3000 = 15000
2P = 15000 – 3000
2P = 12000
P = 6000
PR = 60000
6000 × R = 60000
R = \(\frac{60000}{600}\) = 10 %

Question 25.
கடனாக வழங்கப்பட்ட அசல் ₹ 46,900 க்கு 2 ஆண்டுகளுக்குப் பின் தனிவட்டி மூலம் பெறப்பட்ட மொத்தத் தொகை ₹ 53,466 எனில், வட்டி வீதத்தைக் காண்க
தீர்வு :
P = ₹ 46,900
n = 2 ஆண்டுகள்
A = ₹ 53,466
A = P (1 + \(\frac{\mathrm{nr}}{100}\))

53466 = 46900 (1+ \(\frac{2 r}{100}\))

1 + \(\frac{2 r}{100}\) = \(\frac{53466}{46900}\)

\(\frac{2 r}{100}\) = \(\frac{53466}{46900}\) – 1

= \(\frac{53466-46900}{46900}\)

\(\frac{2 r}{100}\) = \(\frac{6566}{46900}\)

r = \(\frac{6562 \times 100}{46900 \times 2}\)

= \(\frac{6562}{938}\) = 6.9951

r = 7 %

Question 26.
அருண் என்பவர் பாலாஜி என்பவருக்கு ₹ 5,000 ஐ 2 ஆண்டுகளுக்கும் சார்லஸ் என்பவருக்கு ₹ 3,000 ஐ 4 ஆண்டுகுளுக்கு ஒரே தனிவட்டி வீதத்தில் வழங்கினார். ஆக மொத்தமாக ₹2,200 ஐ வட்டியாக அருள் பெற்றார் எனில், வட்டி வீதத்தைக் காண்க.
தீர்வு :
அருண் + சார்லஸ் = மொத்த வட்டி

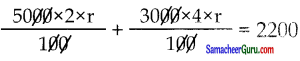
100r + 120r = 2200
220r = 2200
r = \(\frac{2200}{220}\)
r = 10%

Question 27.
ஓர் அசலானது 4 ஆண்டுகளில் இரண்டு மடங்காகிறது எனில், வட்டி வீதத்தைக் காண்க (அசல் : P = ₹100 என வைக்க வேண்டும்).
தீர்வு :
P = ₹ 100
A = ₹ 200, n = 4 ஆண்டுகள்
A = P (1 + \(\frac{\mathrm{nr}}{100}\))

P(1 + \(\frac{\mathrm{nr}}{100}\))

100(1 + \(\frac{1+4 \times r}{100}\)) = 200

1 + \(\frac{\mathrm{nr}}{100}\) = 2

\(\frac{\mathrm{nr}}{100}\) = 2 – 1

\(\frac{\mathrm{nr}}{100}\) = 1

4r = 100
r = \(\frac{100}{4}\)
r = 25%